


 Министерство образования и науки Украины
Министерство образования и науки Украины
Севастопольский национальный технический университет
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК С ПОМОЩЬЮ ПЭВМ
МЕТОДИЧЕСКИЕ рекомендации
для студентов
направления « Инженерная механика »
специальности № 000
очной формы обучения
Севастополь
2008
УДК 531.8
Методические рекомендации к расчетно-графической работе « Расчет перемещений в статически определимых и неопределимых системах » по дисциплине «Сопротивление материалов» для студентов направления « Инженерная механика » специальности № 000 очной формы обучения./ Сост. , - Севастополь: Изд-во СевНТУ, 20с.
Целью методических указаний является оказание помощи студентам при построении эпюр внутренних силовых факторов и расчете перемещений в статически определимых и неопределимых балках с помощью программы Beam 2.2.1.3.
Методические рекомендации рассмотрены на научно-методическом семинаре и утверждены на заседании кафедры технической механики и машиноведения (протокол )
Допущено учебно-методическим центром СевНТУ в качестве методических рекомендаций
Рецензент: , д. т.н., профессор
Введение
Данное методическое указание предназначено для студентов инженерно - технических специальностей дневного отделения. В методическом указании приводятся теоретические основы и пример выполнения расчетно-графического задания по определению перемещений в статически неопределимых стержнях с использованием ЭВМ.
Статически неопределимый стержень или так называемый многопролетный неразрезной стержень нашел большое применение на практике в целях обеспечения большей прочности и жесткости, по сравнению со статически определимыми стержнями, при одинаковых внешних нагрузках.
Теоретические сведения
Пусть заданна статически неопределимая конструкция, схема нагружения которой представлена на рисунке 1.
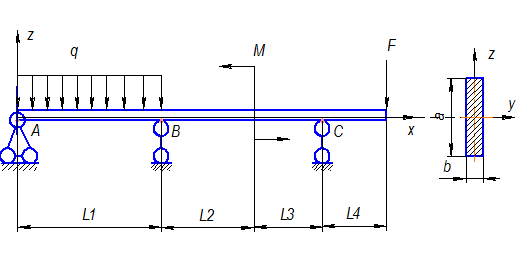
Рисунок 1 – Схема нагруженния конструкции
Граничные условия на каждом краю могут быть:
· жёсткая заделка;
· шарнир;
· свободный край.
Соответственно, если на левом и правом краю балки задан «свободный край», на ней должны быть установлены, по крайней мере, две промежуточные опоры для того, чтобы балка была геометрически неизменяемой.
Соотношения между прогибом, углом поворота сечения и эпюрами M и Q:
- угол поворота сечения
· перерезывающая сила в сечении Q есть производная от изгибающего момента M;
· распределённая нагрузка q есть производная от перерезывающей силы Q
Таким образом, имеют место равенства:
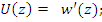 (1)
(1)
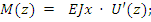 (2)
(2)
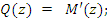 (3)
(3)
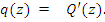 (4)
(4)
При построении эпюр будем руководствоваться формулами (1-4).
Для решения задачи применён метод начальных параметров. Дифференциальное уравнение изогнутой оси балки при этом имеет вид:
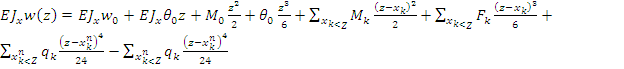 (5)
(5)
где: EJxw0 - прогиб в левом сечении (с точностью до множителя ![]() ); EJxQ0 - угол поворота левого сечения (также с точностью до множителя
); EJxQ0 - угол поворота левого сечения (также с точностью до множителя ![]() ); M0 и Q0 - изгибающий момент и перерезывающая сила в левом сечении.
); M0 и Q0 - изгибающий момент и перерезывающая сила в левом сечении.
Все эти параметры (они называются начальными) - неизвестны. В каждой из сумм суммирование проводится по всем силовым факторам, расположенным слева от текущего сечения. Во второй сумме (сосредоточенных усилий ![]() ) учитываются неизвестные реакции опор R1, R2, .... Таким образом, в уравнении (5) - n+4 неизвестных, где n - количество промежуточных опор. Если все эти неизвестные будут найдены, то будет возможно построить эпюру перемещений по формуле (5) и другие эпюры с помощью производных от (5), которые по (1-3) дают:
) учитываются неизвестные реакции опор R1, R2, .... Таким образом, в уравнении (5) - n+4 неизвестных, где n - количество промежуточных опор. Если все эти неизвестные будут найдены, то будет возможно построить эпюру перемещений по формуле (5) и другие эпюры с помощью производных от (5), которые по (1-3) дают:
углы поворота:
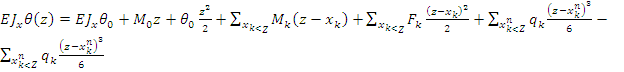 (6)
(6)
изгибающие моменты:
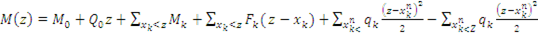 (7)
(7)
перерезывающие силы:
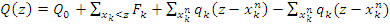 (8)
(8)
Для нахождения этих n+4 неизвестных имеется столько же уравнений:
· под каждой опорой перемещение равно нулю - всего n уравнений вида (5) в тех точках, где расположены опоры;
· по 2 каких-либо параметра на каждом краю балки равны нулю - всего 4 уравнения.
· В зависимости от вида граничных условий будут равны нулю:
· в жёсткой заделке - перемещение и угол поворота;
· при шарнирном закреплении - перемещение и изгибающий момент;
· на свободном краю - изгибающий момент и перерезывающая сила.
При решении задачи будем руководствоваться следующими правилами знаков.
При задании исходных данных будем считать:
· распределённую нагрузку q положительной, если она направлена вверх;
· сосредоточенную нагрузку F положительной, если она направлена вверх;
· сосредоточенный момент M положительным, если он направлен по часовой стрелке.
При построении эпюр будем считать:
· перемещение w положительным, если оно направлено вверх;
· положительный угол поворота θ соответствует возрастанию w;
· положительный изгибающий момент M соответствует возрастанию θ;
· положительная перерезывающая сила Q соответствует возрастанию M;
· положительная распределённая нагрузка q соответствует возрастанию Q.
Пример выполнения расчетно-графического задания
Необходимо: определить перемещения в статически неопределимой балке (см. рис. 1) при следующих входных данных: 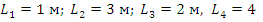 м. Общая длина балки:
м. Общая длина балки: 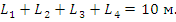
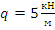 ;
; 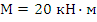 ;
; 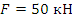 ;
; 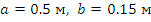 ;
; 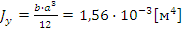 ;
; 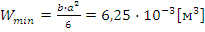 .
.
Запускаем программу Beam 2.2.1.3. После запуска программы на экране монитора появиться главное окно программы:
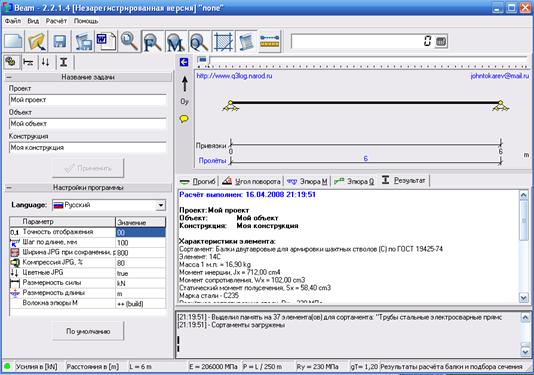
Рисунок 2 – Вид главного меню программы
В главном окне программы можно задать следующие основные параметры:
точность отображения рассчитанных величин; размерность внешних нагрузок; размерность длины. При решении задачи желательно задать следующие настройки:
· точность отображения – 00 (с точностью до второго знака);
· шаг по длине – 1мм;
· размерность силы – кН;
· волокна эпюр – mech.
Для изменения настроек необходимо навести курсор мыши на изменяемый параметр, и произвести нажатие на левую кнопку мыши.
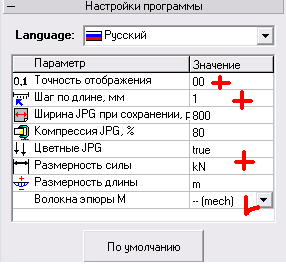
Рисунок 3 – Вид подменю настроек
Шаг 1 – задаем размер балки и устанавливаем опорные узлы:
Выбираем в меню программы подменю – длина балки, условия закрепления.
Рисунок 4 – Вид подменю условий закрепления
После выбора меню в соответствующем поле вводим длину балки в метрах и нажимаем курсором мыши на кнопочку применить.
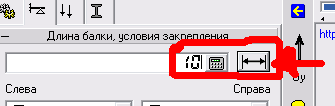
Рисунок 5 – Ввод геометрических характеристик балки
Выбираем поле выбора способа закрепления балки с левого и правого концов. Наводим курсор мыши на соответствующее поле, нажимаем левую кнопку мыши и выбираем необходимый способ закрепления, таким же образом устанавливаем промежуточные опоры.
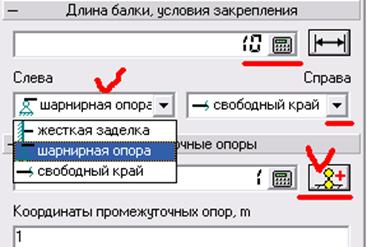
Рисунок 6 – Выбор условий закрепления балки
Шаг 2 – зададим внешние нагрузки
Задание сосредоточенной силы:
Выбираем подменю внешних нагрузок, и выбираем тип нагрузки F.
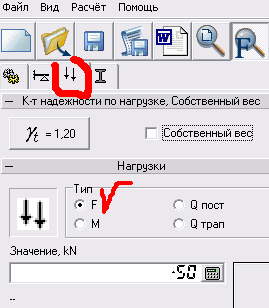
Рисунок 8 – Задание сосредоточенной силы
Выбираем поле «значение» и вводим либо с клавиатуры, либо с помощью мыши значение силы в кН (знак минус говорит о том, что сила направлена вниз). В поле привязка указываем, на каком расстоянии от левого края балки находиться точка приложения силы, в метрах. Нажимаем кнопку установить.
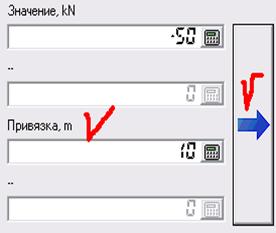 |
Аналогичным образом задается действие сосредоточенного момента и распределенной нагрузки.
Рисунок 9 – Ввод значения сосредоточенной силы и ее привязка
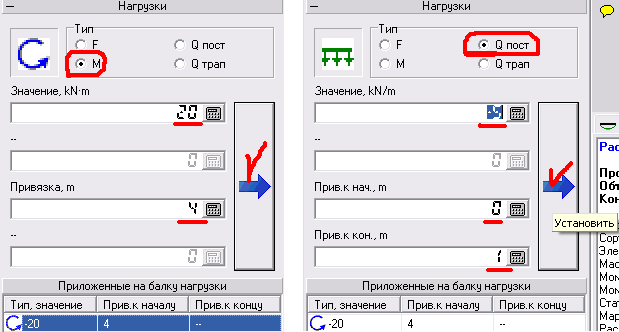
а) б)
Рисунок 10 – а – Ввод сосредоточенного момента, б – ввод распределенной нагрузки
Шаг 3 – подбор сечения и просмотр эпюр
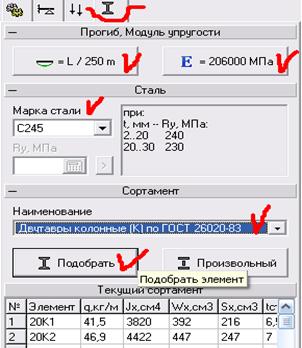 |
Выбираем подменю подбор сечения. В соответствующих окошках задаем: марку материала, профиль сечения, допустимый прогиб и модуль упругости материала. За тем, курсором мыши, нажимаем кнопку подобрать.
Рисунок 11 – Подбор стандартного сечения
Примечания: в программе есть возможность задавать как стандартный профиль, так и произвольный.
Для задания произвольного сечения необходимо в меню – произвольное сечение указать расчетное значение момента инерции ![]() и момента сопротивления
и момента сопротивления ![]() . В полях масса погонного метра, толщина стенки, статический момент полусечения можно указать «1», так как эти параметры не влияют на построение эпюры прогиба и эпюры моментов.
. В полях масса погонного метра, толщина стенки, статический момент полусечения можно указать «1», так как эти параметры не влияют на построение эпюры прогиба и эпюры моментов.
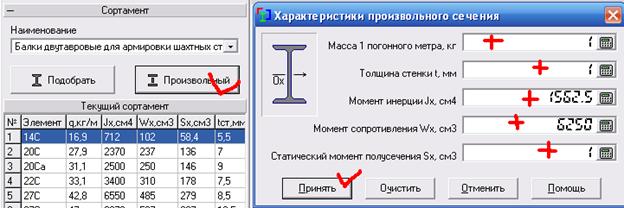
Рисунок 12 – Ввод характеристик произвольного сечения
Для просмотра эпюр необходимо в главном меню выбрать вкладку просмотра соответствующей эпюры см. рис.13, 14.
Расчетное значение неизвестных опорных реакций указываются рядом с опорой. 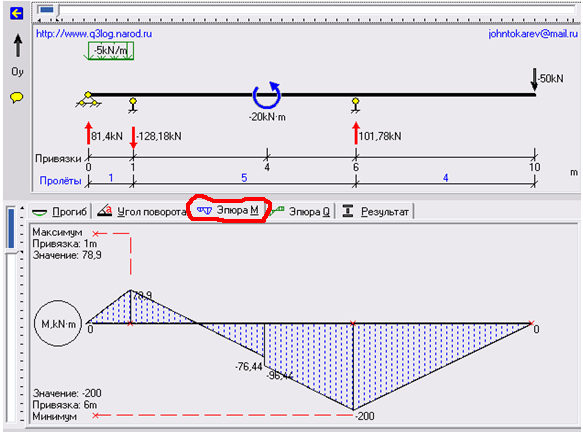
Рисунок 13 – Просмотр эпюры изгибающих моментов
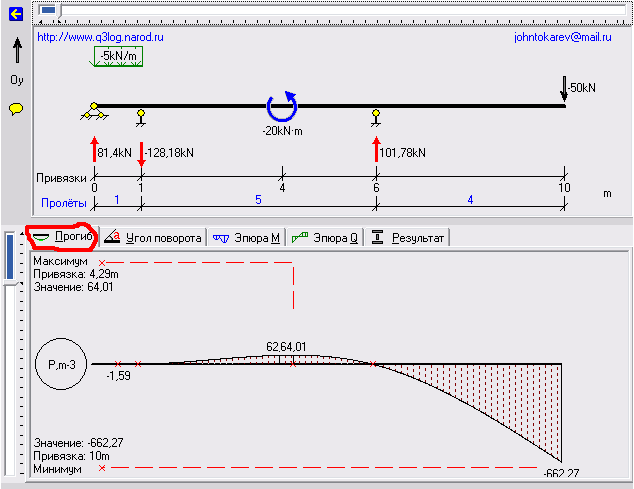
Рисунок 14 – Просмотр эпюры прогиба балки





