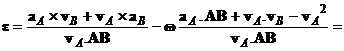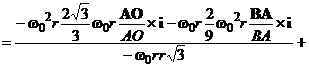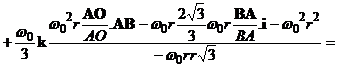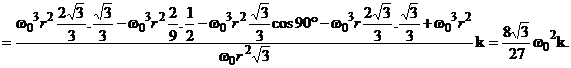УДК 531.1/2
СТ. Н.БЪЧВАРОВ, В. Д.ЗЛАТАНОВ
ОБ ОПРЕДЕЛЕНИЯ ВЕКТОРА УГЛОВОГО УСКОРЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
1. Введение
Известно, что скорость ![]() произвольной точки М абсолютно твердого тела определяется формулой
произвольной точки М абсолютно твердого тела определяется формулой
| (1) |
называемой законом распределения скоростей точек тела.
Вектор ![]() в формуле (1), называемый вектором угловой скорости тела, не зависит от выбора точки М и полюса А и является важной кинематической характеристикой движения.
в формуле (1), называемый вектором угловой скорости тела, не зависит от выбора точки М и полюса А и является важной кинематической характеристикой движения.
Введение вектора угловой скорости ![]() осуществляется в основном двумя способами. Первый способ основан на понятии вектора бесконечно малого поворота тела. Обычно сначала рассматривается твердое тело с одной неподвижной точкой А и двумя бесконечно близкими положениями, соответствующими моментам
осуществляется в основном двумя способами. Первый способ основан на понятии вектора бесконечно малого поворота тела. Обычно сначала рассматривается твердое тело с одной неподвижной точкой А и двумя бесконечно близкими положениями, соответствующими моментам ![]() и
и ![]() . Перемещение
. Перемещение ![]() произвольной точки М тела перпендикулярно вектору
произвольной точки М тела перпендикулярно вектору 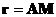 . Вводится вектор
. Вводится вектор ![]() таким образом, что
таким образом, что ![]() , и после этого из равенства
, и после этого из равенства ![]() определяется вектор
определяется вектор ![]() . Пусть точка А движется скоростью
. Пусть точка А движется скоростью ![]() . Вводится система координат, имеющая начало в точке А и перемещающаяся поступательно со скоростью
. Вводится система координат, имеющая начало в точке А и перемещающаяся поступательно со скоростью ![]() . Движение тела складывается из переносного поступательного движения со скоростью
. Движение тела складывается из переносного поступательного движения со скоростью ![]() и относительного вращательного движения вокруг точки А. В результате этого сложения получается формула (1) ([2], [6], [9], [10] и др.). Введение вектора бесконечно малого поворота можно осуществить в соответствии с теоремами конечного поворота Эйлера и Шаля и пользуясь осью конечного поворота тела ([14], [16]). Подробнее теория конечного поворота тела изложена в [7].
и относительного вращательного движения вокруг точки А. В результате этого сложения получается формула (1) ([2], [6], [9], [10] и др.). Введение вектора бесконечно малого поворота можно осуществить в соответствии с теоремами конечного поворота Эйлера и Шаля и пользуясь осью конечного поворота тела ([14], [16]). Подробнее теория конечного поворота тела изложена в [7].
Другой часто встречающийся способ введения вектора ![]() основан на том, что с твердым телом связан подвижной триэдр
основан на том, что с твердым телом связан подвижной триэдр ![]() . Для единичных векторов
. Для единичных векторов ![]() имеем
имеем
| (2) |
Во время движения твердого тела единичные векторы ![]() , постоянные по модулю, меняют свои направления, и поэтому
, постоянные по модулю, меняют свои направления, и поэтому ![]() . Производная
. Производная ![]() представляется в виде
представляется в виде
| (3) |
На основании соотношения (2) имеем ![]() , поэтому
, поэтому ![]() , откуда следует, что
, откуда следует, что ![]() . Коэффициенты
. Коэффициенты ![]() представляют собой компоненты кососимметрического тензора, которому сопоставляется вектор
представляют собой компоненты кососимметрического тензора, которому сопоставляется вектор ![]() , причём
, причём ![]() . Тогда формулы (3) принимают известный вид:
. Тогда формулы (3) принимают известный вид:
| (4) |
Радиус-вектор ![]() , соединяющий некоторую неподвижную точку О с произвольной точкой М тела, представлен как векторная сумма радиус-вектора полюса
, соединяющий некоторую неподвижную точку О с произвольной точкой М тела, представлен как векторная сумма радиус-вектора полюса 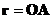 и радиус-вектора
и радиус-вектора ![]() , определяющего положение точки М относительно полюса А, т. е.
, определяющего положение точки М относительно полюса А, т. е. 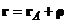 . Здесь вектор
. Здесь вектор ![]() неизменно связан с телом и поэтому координаты
неизменно связан с телом и поэтому координаты ![]() постоянны во времени. Дифференцируя
постоянны во времени. Дифференцируя 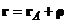 и используя соотношения (4), приходим к формуле (1) . Этот способ в каком-то смысле более формальный, но с другой стороны предлагает возможность связывания вектора
и используя соотношения (4), приходим к формуле (1) . Этот способ в каком-то смысле более формальный, но с другой стороны предлагает возможность связывания вектора ![]() с углами Эйлера.
с углами Эйлера.
В середине прошлого столетия болгарский ученый Аркадий Стоянов опубликовал несколько работ на тему “О кинематике идеально твердого тела” [11,12], результаты которых представлены в [13]. В них кинематика общего движения абсолютно твердого тела представлена дедуктивным способом, без использования метода подвижного триэдра, формул (4) Пуансона и вектора бесконечно малого поворота. Принимается, что общее движение твердого тела в пространстве определяется движением трех точек ![]() не лежащих на одной прямой. Решалась следующая задача: в данный момент времени известны скорости
не лежащих на одной прямой. Решалась следующая задача: в данный момент времени известны скорости ![]() трех “основных” точек
трех “основных” точек ![]() ; требуется определить скорость произвольной точки М этого тела. Решением этой задачи стала формула для определения вектора угловой скорости
; требуется определить скорость произвольной точки М этого тела. Решением этой задачи стала формула для определения вектора угловой скорости ![]() тела при помощи скоростей трех точек и их взаимных положений [13]
тела при помощи скоростей трех точек и их взаимных положений [13]
| (5) |
Доказательство этой формулы следует непосредственно из закона распределения скоростей (1). Выражая последовательно скорости “основных” точек, имеем
|
Векторно умножая равенства слева на ![]() соответственно и складывая, получаем
соответственно и складывая, получаем
|
Здесь принято во внимание, что ![]() , и, учитывая равенство
, и, учитывая равенство ![]() , получаем равенство (5).
, получаем равенство (5).
2. Цель исследования
Цель настоящей работы – определить вектор углового ускорения тела ![]() , если известны скорости
, если известны скорости ![]() и ускорения
и ускорения ![]() трех “основных точек”
трех “основных точек” 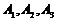 в данный момент времени.
в данный момент времени.
3. Определение вектора углового ускорения
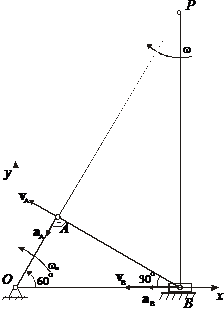
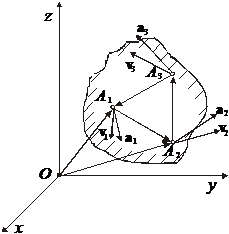
Определим вектор углового ускорения ![]() твердого тела в общем случае его движения (рис. 1). Представляем формулу (5) в виде
твердого тела в общем случае его движения (рис. 1). Представляем формулу (5) в виде
|
и дифференцируем по времени
| (6) |
|
|
Рис. 1. Общий случай движения твердого тела |
|
Имея в виду, что
| (7) |
подставляя (7) в (6) и совершая несложные преобразования, получаем для вектора углового ускорения
| (8) |
где вектор угловой скорости ![]() нужно выразить при помощи (5). Полученной формулой (8) определяется вектор углового ускорения
нужно выразить при помощи (5). Полученной формулой (8) определяется вектор углового ускорения ![]() через скорости
через скорости ![]() и ускорении
и ускорении ![]() трех неколлинеарных основных точек
трех неколлинеарных основных точек ![]() , в предположении, что движение этих точек известно.
, в предположении, что движение этих точек известно.
4. Частные случаи движения твердого тела
Рассмотрим определение углового ускорения ![]() в случаях, когда на движение твердого тела наложены некоторые ограничения.
в случаях, когда на движение твердого тела наложены некоторые ограничения.
· Поступательное движение твердого тела. В случае поступательного движения: скорости и ускорения всех точек тела равны между собой
| (9) |
Подставляя (9) последовательно в (5) и (8) получаем
| (10) |
т. е. векторы ![]() и
и ![]() при поступательном движении тела равны нулю.
при поступательном движении тела равны нулю.
· Вращательное движение твердого тела вокруг неподвижной оси. Это движение твердого тела, при котором две точки ![]() и
и ![]() тела неподвижны. Прямая, определённая этими точками, называется неподвижной осью тела. Теперь движение тела определяется движением только одной точки
тела неподвижны. Прямая, определённая этими точками, называется неподвижной осью тела. Теперь движение тела определяется движением только одной точки ![]() , находящейся вне оси вращения
, находящейся вне оси вращения 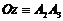 (рис. 2).
(рис. 2).
|
Рис. 2. Вращательное движение |
Тело абсолютно твердое, поэтому
|
после дифференцирования по времени имеем
|
потому что 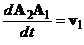 и
и 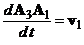 . Из этого следует, что
. Из этого следует, что ![]() и
и ![]() , т. е. скорость
, т. е. скорость ![]() любой точки тела вне оси вращения перпендикулярна плоскости, определённой этой точкой и этой осью. Поэтому введём вектор
любой точки тела вне оси вращения перпендикулярна плоскости, определённой этой точкой и этой осью. Поэтому введём вектор ![]() , направленный по оси вращения, таким образом, чтобы его векторное произведение на
, направленный по оси вращения, таким образом, чтобы его векторное произведение на ![]() или
или ![]() равнялось
равнялось ![]() , т. е.
, т. е.
| (11) |
Здесь О – произвольная точка на оси. Если размерность ![]() – м/с, размерность
– м/с, размерность ![]() – м и размерность
– м и размерность![]() – с-1, то коэффициент пропорциональности перед векторным произведением в правой части равенства равняется единице.
– с-1, то коэффициент пропорциональности перед векторным произведением в правой части равенства равняется единице.
Обозначим ![]() ортогональную проекцию точки
ортогональную проекцию точки ![]() на ось вращения
на ось вращения ![]() и представим вектор
и представим вектор ![]() как
как ![]() . Тогда формула (11) примет вид
. Тогда формула (11) примет вид![]()
| (12) |
где 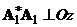 . Умножаем обе части равенства слева векторно на
. Умножаем обе части равенства слева векторно на ![]()
|
или
|
и так как 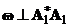 , находим
, находим
| (13) |
Дифференцируя по времени, получаем
| (14) |
где ![]() – ускорение точки
– ускорение точки ![]() ,
, 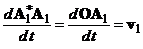 , а
, а 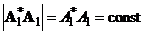 .
.
· Плоскопараллельное движение тела. В этом случае каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости ![]() (плоскость движения). Для задания плоскопараллельного движения тела достаточно задать движение какого-либо сечения тела плоскостью, параллельной плоскости
(плоскость движения). Для задания плоскопараллельного движения тела достаточно задать движение какого-либо сечения тела плоскостью, параллельной плоскости ![]() (рис. 3). Положение и движение этой плоской фигуры в ее плоскости
(рис. 3). Положение и движение этой плоской фигуры в ее плоскости ![]() вполне определяется двумя точками
вполне определяется двумя точками ![]() и
и ![]() , причём
, причём
|
|
|
|
Рис.3. Плоскопараллельное движение |
|
Дифференцируем последнее соотношение по времени и находим
|
так как 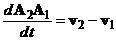 . Отсюда следует, что разность скоростей
. Отсюда следует, что разность скоростей ![]() точек
точек ![]() и
и ![]() в любой момент времени перпендикулярна прямой, соединяющей эти точки. Введём вектор
в любой момент времени перпендикулярна прямой, соединяющей эти точки. Введём вектор ![]() , перпендикулярный плоскости движения, таким образом, чтобы разность скоростей
, перпендикулярный плоскости движения, таким образом, чтобы разность скоростей 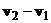 равнялась векторному произведению вектора угловой скорости
равнялась векторному произведению вектора угловой скорости ![]() на
на ![]() , т. е.
, т. е.
| (15) |
После векторного умножения второго векторного равенства (15) на ![]() , имея в виду, что
, имея в виду, что ![]() , для вектора угловой скорости
, для вектора угловой скорости ![]() получаем
получаем
| (16) |
а после векторного умножения первого равенства (15) на ![]() и учитывая, что
и учитывая, что ![]() , получаем формулу для определения вектора
, получаем формулу для определения вектора ![]() при помощи скоростей точек
при помощи скоростей точек ![]() и
и ![]() плоской фигуры тела
плоской фигуры тела
| (17) |
Из равенств (16) и (17) находим два выражения для определения углового ускорения ![]() плоской фигуры тела скоростями и ускорениями точек
плоской фигуры тела скоростями и ускорениями точек ![]() и
и ![]() этой фигуры.
этой фигуры.
Дифференцируя по времени формулу (16), имеем
| (18) |
где ![]() можно получить из формулы (17).
можно получить из формулы (17).
Дифференцируя по времени формулу (17), получаем
| (19) |
где вектор ![]() определяется только ускорениями
определяется только ускорениями ![]() точек
точек ![]() и
и ![]() , а также их взаимным положением.
, а также их взаимным положением.
· Движение твердого тела, имеющего одну неподвижную точку. В этом случае точки тела движутся по поверхностям сфер с центром в неподвижной точке ![]() (рис. 4).
(рис. 4).
|
Рис.4. Движение тела имеющего одну неподвижную точку |
Движение тела вполне определяется движением сферической фигуры, полученной пересечением тела со сферой с центром ![]() . С другой стороны движение этой сферической фигуры определяется движением её двух точек
. С другой стороны движение этой сферической фигуры определяется движением её двух точек ![]() и
и ![]() . Пусть третья основная точка – это неподвижная точка
. Пусть третья основная точка – это неподвижная точка ![]() . Тогда имеем
. Тогда имеем
|
Дифференцируя по времени, получаем
|
т. е. во время движения
|
так как 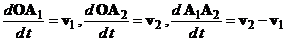 . Имеем
. Имеем
|
Векторно умножая третье равенство слева на ![]() , снова получаем
, снова получаем
| (20) |
В формуле (20), в отличие от формулы (16), скорости ![]() и
и ![]() точек
точек ![]() и
и ![]() не всегда перпендикулярны одной неподвижной оси.
не всегда перпендикулярны одной неподвижной оси.
Дифференцируя (20) по времени, имеем
| (21) |
причём скорости ![]() и
и ![]() и ускорения
и ускорения ![]() и
и ![]() точек
точек ![]() и
и ![]() не всегда перпендикулярны одной неподвижной оси, как это было в случае плоскопараллельного движения.
не всегда перпендикулярны одной неподвижной оси, как это было в случае плоскопараллельного движения.
5. Пример
Рассмотрим кривошипно-ползунный механизм (рис. 5). Кривошип ОА длиной ![]() вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью ![]() . Определить угловую скорость
. Определить угловую скорость ![]() и угловое ускорение
и угловое ускорение ![]() шатуна АВ при
шатуна АВ при ![]() и
и ![]() .
.
Шатун совершает плоское движение. Для скоростей и ускорений основных точек А и В (АºА1, ВºА2 ) имеем
|
где 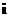 – единичный вектор оси
– единичный вектор оси ![]() , а
, а ![]() и
и ![]() единичные векторы, определяющие направлений скоростей
единичные векторы, определяющие направлений скоростей ![]() и
и ![]() .
.
Используя формулу (16) и имея ввиду, что ![]() , получаем угловую скорость
, получаем угловую скорость ![]() шатуна АВ
шатуна АВ
|
|
|
|
Рис.5. Кривошипно-ползунный механизм |
|
Для определения углового ускорения ![]() шатуна воспользуемся формулой (18). Имея в виду, что
шатуна воспользуемся формулой (18). Имея в виду, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 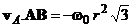 , получаем
, получаем
|
|
|
|
Векторы ![]() и
и ![]() перпендикулярны плоскости движения. Знак “–“ перед
перпендикулярны плоскости движения. Знак “–“ перед ![]() указывает, что вращение шатуна совершается в данный момент времени по часовой стрелке, а “+” перед
указывает, что вращение шатуна совершается в данный момент времени по часовой стрелке, а “+” перед ![]() , что шатун вращается замедленно, и вектор направлен к наблюдателю.
, что шатун вращается замедленно, и вектор направлен к наблюдателю.
Полученные результаты совпадают с результатами решения этих задач при помощи мгновенного центра скоростей и законов распределения скоростей и ускорений.
6. Заключение
После краткого обзора принятых в литературе способов введения вектора угловой скорости в кинематике абсолютно твердого тела в работе представлена формула для вычисления угловой скорости ![]() по трём точкам, не лежащим на одной прямой. На основании этой формулы получены формулы для определения углового ускорения
по трём точкам, не лежащим на одной прямой. На основании этой формулы получены формулы для определения углового ускорения ![]() в общем случае движения твёрдого тела и в частных случаях, с использованием скорости и ускорения трех “основных” точек. Применение полученных формул проиллюстрировано на примере кривошипно-шатунного механизма. Результаты совпадают с результатами решения этих задач традиционными методами.
в общем случае движения твёрдого тела и в частных случаях, с использованием скорости и ускорения трех “основных” точек. Применение полученных формул проиллюстрировано на примере кривошипно-шатунного механизма. Результаты совпадают с результатами решения этих задач традиционными методами.
СПИСОК ЛИТЕРАТУРЫ
1. Теоретическая механика, т. І. - М.: Физматгиз, 1960.-515 с.
2. Основной курс теоретической механики, т. І. - М.: Наука, 1965.-467 с.
3. Механика, ч. І. - С.: Стандартизация принт, 2001.-391 с.
4. Механика. - М.: РХД 2001.-368 с.
5. Е. Векторное исчисление и начала тензорного исчисления. - М.: Наука, 1965.-424 с.
6. , Механика. - М.: Наука, 1988.-215 с.
7. Аналитическая механика. - М.: Физматгиз, 1961.-824 с.
8. Курс по теоретична механика, ч. І. - С.: Техника, 1974.-427 с.
9. Розе Н.В. Теоретическая механика І. - Л.-М.: Гостехиздат, 1933.-428 с.
10. Синг Дж.Л. Классическая механика. - М.: Физматгиз, 1963.-448 с.
11. Върху кинематиката на твърдо тяло. - Годишник на Държавната политехника, т. ІІІ, кн. І, С. 1950.
12. Върху кинематиката на абсолютно твърдото тяло, ІІ. - Годишник на ИСИ, т. V, С. .
13. Теоретична механика, ч. ІІ Кинематика и динамика. - С.: Наука и изкуство, 1953, 1956.
14. К. Теоретическая механика. - М.: Гостехиздат, 19с.
15. О распределении скоростей в твердом теле. - Республиканский межведомственный сборник “Механика твердого тела”.– Киев: Наукова думка, 1969.-с 77-81.
16. Т. Аналитическая динамика. - М.-Л.:ОНТИ, 1937.-586 с.
Поступила в редакцию 13.02.2007
После доработки 10.03.2007



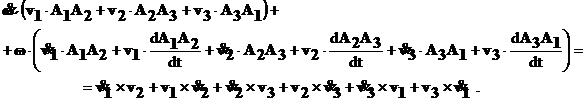
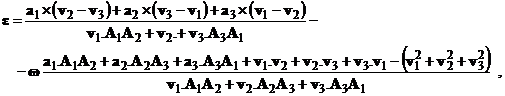

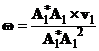 .
.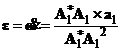 ,
,
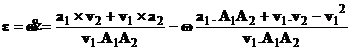 .
.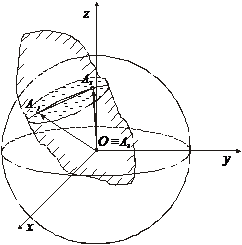
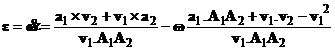 ,
,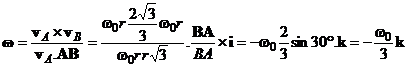 .
.