Альтернативный подход
к изучению понятия вектора
в физике 7-11 классов
учителя физики МОУ «Новосокольническая
средняя общеобразовательная школа»
,
На современном этапе развития среднего образования наметилась тенденция к сокращению числа часов, предназначенных для изучения физики и математики в школе; учителям самим приходится принимать различные меры, чтобы и в данных условиях, по возможности, не допускать снижения уровня физико-математической подготовки выпускников школ.
Наблюдая за учениками на уроках физики, можно отметить, что у них часто возникают трудности (особенно при решении задач) чисто математического плана. Жёсткие рамки программ, нехватка времени, большой объём изучаемого материала – вот некоторые причины возникновения подобных трудностей.
Математика и физика считаются наиболее трудными предметами
школьного курса. Но эти предметы развивались взаимосвязано. Непонимание математики ведет за собой непонимание физики. Физика насквозь пронизана математикой. Непонимание школьниками какого-либо вопроса из курса физики или неумение решить физическую задачу связано с отсутствием навыков анализа функциональных зависимостей, составлением и решением математических уравнений, неумением проводить алгебраические и геометрические построения. Русский ученый о том, как математика помогает физике писал, так: «Ни одна из естественных наук, если дело идет не о собирании материала, а о действительном творчестве, не обойдется без математики – матери всех других наук. Что же касается физики, поставленной впереди всех других наук… то в настоящее время математика и физика до такой степени слились в одно целое, что иногда трудно отделить – где кончается физика и начинается математика».
В ряде случаев новые математические понятия вводятся на уроках
физики раньше, чем математики.
Имеют место случаи, когда чисто математические понятия в математике не рассматриваются, а в физике вводятся и используются.
Одним из ключевых связующих звеньев между математикой и физикой является понятие векторной величины.
Например, в курсе геометрии подробно рассматриваются операции сложения вычитания векторов, умножение вектора на число, и совершенно отсутствует понятие проекции вектора на ось.
В 9 классе учащиеся на уроках математики приобретают необходимые навыки выполнения операций над векторами, которые облегчают изучение механики (кинематики и динамики) на векторной основе. Однако порой школьники затрудняются выполнять действия по преобразованию векторных уравнений: переносить слагаемые из одной части уравнения в другую, умножать левую и правую части уравнения на число.
В курсе геометрии вводится понятие координат вектора, вводятся формулы, связывающие координаты вектора с его модулем и углом, который вектор составляет с положительным направлением оси абсцисс, изучают скалярное произведение векторов.
Между тем, с основными характеристиками вектора ребенок знаком с дошкольного возраста: «туда нельзя», «сколько тебе лет», «зачем кошку за хвост таскал?» и т. д. Подобных «намеков» на направление, численное значение и точку приложения достаточно много наберется и в начальной школе. Но впервые наиболее акцентированно с понятием вектора мы знакомим ребенка на уроках физики в 7 классе.
Понятие вектора в различных учебниках вводится по-разному.
Проследим его введение по линии учебников физики для основной школы, созданных одним коллективом авторов: , , .
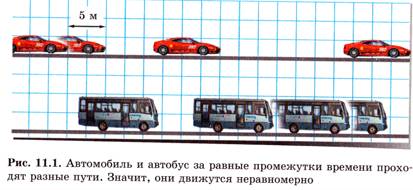
В учебнике «Физика - 7» (§ 4) вводится понятие числового значения физической величины, затем речь идет об измерительных приборах, цене деления (масштаб), измерении длины, оценке размеров молекул и их скорости (§ 5, 6), схематическое изображение сил отталкивания между молекулами стрелками, длина траектории, обозначение пути (§ 8), сравнение физических величин (равные пути, равные промежутки времени (§ 9)). И наконец, в § 9 дается формула вычисления скорости, указано обозначение пути буквой L, указан способ изображения направления скорости - стрелкой, где «длина стрелки пропорциональна значению скорости». Но обозначение скорости и времени буквами v и t не оговаривается.

При работе по рисунку 9.1 у учащихся возникают вопросы:
1) Где рисовать стрелку?
2) Почему скорость грузовика 10 м/с и скорость легковой машины 15 м/с?
Далее предлагается учащимся решить задачу: «Андрей проехал на велосипеде 300м за 1 минуту. С какой скорость он ехал?» Зададим вопрос себе - Что мы хотим узнать у учащегося? Только числовое значение!
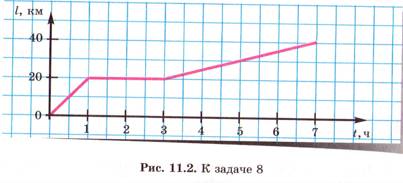
Все последующие задачи направлены на нахождение только числового значения физических величин. Зачем тогда мы говорим о направлении скорости, если в предложенных задачах учебника нас интересует ответ на вопрос – сколько, а ребенок не видит на рисунке указанный масштаб, забытый с 6 класса. Видно противоречие между рисунками (с указанием направления скорости) и условиями задач. Вероятно, авторы предполагают, что учащийся увидел масштаб по длине стрелок, но этого не происходит. Аналогично рисунки 11.1 и 11.2 предполагают знание масштаба
Оставим вопросы без ответа и перейдем к § 14. В § 14 «Силы. Сила тяжести» вводятся определение силы, числовое значение силы (модуль), направление силы, дается определение векторной величины. «Силы обозначают стрелками (направленными отрезками). Начало стрелки совпадает с точкой приложения силы. Стрелка показывает направление силы. Длина стрелки пропорциональна мод.3, 14.4

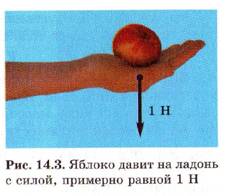
Далее предлагается задача: «Чему равна сила тяжести школьника массой 40кг?» И здесь, как и при введении скорости предлагается получение числа. Опять возникают те же вопросы.
В учебнике 7 класса хорошо изображены на рисунках силы, с фиксированными направлениями, точки приложения, иногда используются цветовые изображения различных сил.
Понятно, что если мы напомним учащимся о масштабе, цене деления, то уже в 7 классе можем ввести полноценное определение вектора, четко разведя понятия «изображение» вектора и «обозначение» вектора. Тогда ученик будет осмысленно и однозначно пользоваться понятием вектора, не дожидаясь его введения в 9 классе. «Числовое значение векторной величины называют модулем этой величины. Обозначают векторную величину буквой со стрелкой… Модуль вектора обозначают той же буквой, но без стрелки…
На чертежах векторные величины изображают стрелками.
Величины, которые характеризуются только числовым значением, называют скалярными. Примерами скалярных величин являются путь и время».
К сожалению, программа 8 класса предполагает возвращение к теме векторной величины при изучении закона Кулона только в виде формулы. Где опять возникают вопросы. Почему не оговариваем характеристики силы, как векторной величины?
В 10 и 11 классах понятие вектора становится снова востребованным при изучении большинства тем, в которых особенно ярко проявляют себя указанные выше неточности. Наибольшие затруднения вызывают задачи, предполагающие четкое представление о точке приложения силы.
С целью решения обозначенных трудностей предлагаем своего рода кодификатор понятия векторной величины, опираясь на ассоциативное и цветовое восприятие школьником изучаемого материала.
С первых уроков физики с семиклассниками, например, через пословицы настраиваем их на внимательное и осторожное отношение к различным физическим величинам.
Кодификатор можно использовать как на уроках физики, так и на уроках математики в течение всего учебного года при различных видах деятельности.





