Как рассчитать доходность и показатели эффективности инвестирования с учетом риска

Как рассчитать доходность и показатели эффективности инвестирования с учетом риска

Существует два подхода к расчету доходности.

- Процентная доходность с момента времени t до момента i: ,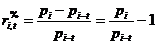

где pi – цена в i-ый период времени.

- Логарифмическая доходность с момента времени t до момента i: .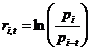

При работе с финансовыми активами довольно часто используют логарифмическую доходность. Преимущество ее использования двояко:

Во-первых, она может быть экономически более содержательной, чем процентная доходность. Если логарифмическая доходность распределена нормально, то распределение никогда не приведет к отрицательной цене. Это потому, что в левом хвосте распределения логарифмы отношения цен стремятся к «минус бесконечности» при текущей цене, стремящейся к нулю. Напротив, в левом хвосте нормально распределенной процентной доходности величина стремится к «минус бесконечности» при отрицательной величине текущей цены. Экономически это бессмысленно.

Второе преимущество логарифмических доходностей состоит в том, что они хорошо агрегируются во времени. Логарифмическая доходность от момента времени t до момента времени T эквивалентна сумме логарифмических доходностей на интервалах от t до t и от t до T, где :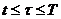

.

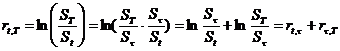Эта временная аддитивность логарифмических доходностей говорит о том, что если однопериодные доходности независимы, то волатильность доходностей масштабируется на квадратный корень из времени ().

Однако, процентные доходности имеют хорошие свойства для тех случаев, когда мы хотим агрегировать активы в портфель. Например

,

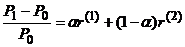где a - доля портфеля, вложенная в акцию, r(1) - доходность акции, r(2) - доходность облигации, Pi – стоимость портфеля в i-ый момент времени. В то же время логарифмическая доходность портфеля не является средневзвешенным логарифмических доходностей активов, входящих в портфель.

Рассмотрев особенности каждого типа доходностей, приходим к выводу, что выбор в пользу того или иного типа приводит нас к отказу или от возможности агрегирования активов в портфель, или от возможности агрегирования по времени.

Стандартное отклонение дневных доходностей рассчитывается по формуле:

,

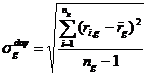Где - число наблюдений доходности в g-ом году,

– дневная логарифмическая доходность в i-ый день в g-ом году,

- средняя доходность за g-ый год, рассчитанная по формуле .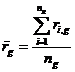

В знаменателе формулы фигурирует (-1), так как мы имеем дело не с генеральной совокупностью, а с выборкой.

Для расчета недельной волатильности используется та же формула, но только доходность берется недельная (на недельном отрезке времени).

Коэффициент Шарпа, так же как и Сортино, служит для сравнения различных инвестиционных активов (а чаще всего портфелей) между собой по критерию «риск-доходность». Коэффициенты показывают, какую доходность приносит актив на единицу риска.

Формулы для расчета дневного[1], недельного и месячного коэффициента Шарпа:

;

;

.

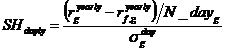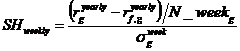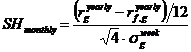Здесь - число доходностей в g-ом году;

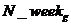- число недель в g-ом году;

- стандартное отклонение на основе дневных доходностей в g-ый год;

- стандартное отклонение на основе недельных доходностей в g-ый год;

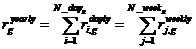- доходность в g-ый год,

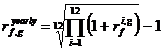- средняя годовая ставка без риска. Здесь - безрисковая ставка доходность в i-ый месяц в g-ом году.

Коэффициент Шарпа имеет определенные недостатки. Во-первых, это связано с определением риска «двухсторонней волатильности», определяемой в виде стандартного отклонения доходностей от среднего значения. Дело в том, что фонды с положительным колебанием доходности и с отрицательным колебанием доходности при прочих равных могут иметь близкий по значению показатель волатильности, что с инвестиционной точки зрения не корректно. Отчасти этот недостаток позволяет элиминировать коэффициент Сортино, который учитывает только отрицательные колебания доходности. Таким образом, исключает положительные изменения в доходности, которые не создают для инвестора риска потерь.

Еще один недостаток который позволяет преодолеть коэффициент Сортино заключается в том, что коэффициент Шарпа построен на основе модели CAPM и предпосылок о нормальности распределения доходности, но это не всегда так. Чтобы проверить, насколько распределение близко к нормальному, рассчитаны показатели асимметрии и эксцесса по выделенным инвестиционным активам (портфелям).

Знаменатель в формуле коэффициента Сортино имеет следующий вид:

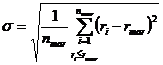
Где - минимально допустимая доходность (в нашем случае она мы будем брать ее равной нулю)

- количество наблюдений, в которые доходность была ниже или равна .

В знаменатели учитываются только те значения , которые были ниже или равны .

Асимметрия и эксцесс, наравне с математическим ожиданием и дисперсией, являются характеристиками плотности распределения случайной величины.

[1] При определении волатильности за год на основе дневных данных можно допустить существенную погрешность, особенно если стандартное отклонение следует процессу "mean reversion" (возвращение к среднему). Волатильность в долгосрочной перспективе испытывает колебания вокруг среднего значения, а не возрастает бесконечно пропорционально величине корень из Т. (см Буренин портфелем ценных бумаг, М.,2008, стр.18). Исходя из этого для расчета коэффициента Шарпа за неделю и месяц берется недельная волатильность.