ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теоретическая механика – это наука, изучающая математические методы расчёта механизмов и сооружений. Расчет ведется не самих реальных объектов, а их моделей. Применяют графический и аналитический методы расчета.
Графический метод – основан на геометрических построениях.
Аналитический метод – основан на алгебраических расчетах.
Статика – это раздел теоретической механики, который изучает равновесие абсолютно твердых тел под действием сил.
Абсолютно твердое тело – это недеформируемое тело, в котором расстояние между любыми двумя точками всегда остается неизменным и никакие внешние воздействия не вызывают изменения его размеров и формы.
Лекция №1
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ
1.1 Сила и система сил
Сила – это мера механического воздействия одного тела на другое. Сила измеряется в ньютонах (Н) и является векторной величиной, то есть характеризуется 1) численным значением (модулем);
2) точкой приложения;
3) направлением.
В графическом методе расчета силу изображают в виде вектора, в каком либо масштабе.
Пример1.1. Начертить вектор силы F = 30 кН в масштабе 1:5.
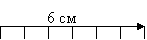Решение. Составляем пропорцию:
|
Пример 1.2. Определить значение силы, если в масштабе 1:2 вектор имеет длину 3 см.
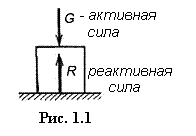Решение: составляем пропорцию:
|
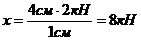
Силы бывают внешними и внутренними.
Внешние силы представляют собой действие одного тела на другое и
делятся на активные и реактивные.
Активные силы – стремятся вызвать перемещение тела (сила G, рис. 1.1).
Реактивные силы (реакции) – стремятся противодействовать перемещению тела под действием активных сил (сила R, рис. 1.1).
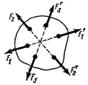Внутренние силы - возникают внутри тела под действием внешних сил.
Система сил - совокупность нескольких сил, приложенных к телу.
Плоская система сил - линии действия сил лежат в одной плоскости.
Пространственная система сил - линии действия сил лежат в разных плоскостях.
|
Эквивалентные системы сил – разные системы сил, которые оказывают одинаковое механическое действие на тело.
Равнодействующая сила - одна сила, эквивалентная данной системе сил.
Уравновешивающая сила - сила, равная по модулю данной силе и направленная по той же линии действия, но в противоположную сторону.
Уравновешенная система сил - система сил, приложенная к материальной точке под воздействием которой точка находится в состоянии покоя.
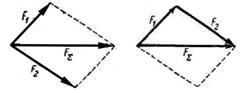Правило параллелограмма - равнодействующая (FΣ) двух сил (F1 и F2), приложенных к одной точке, является диагональю параллелограмма, построенного на данных силах (рис. 1.3, а). Вместо правила параллелограмма можно пользоваться правилом треугольника (рис. 1.3, б).
|
Få2= F12 + F22 + 2 F1 × F2cosj
1.3 Связи и их реакции
Связи - это тела, которые ограничивают движение рассматриваемого тела.
Реакции связей - силы, действующие на тело со стороны связей, которые противодействуют возможным движениям тела. Реакция связи всегда противоположна направлению, по которому возможно движение тела.
Принцип освобождения от связей - не изменяя равновесия тела, каждую связь можно отбросить, заменив ее реакцией.
Наиболее распространенные виды связей:
1) Связь в виде гладкой плоскости (рис. 1.4, а). Реакция связи (R) направлена перпендикулярно к опорной поверхности.
2) Гибкая связь, осуществляемая веревкой, тросом, цепью и т. п. (рис. 1.4, б). Реакции гибких связей RA и RB направлены вдоль связей.
3) Связь в виде жесткого прямого стержня с шарнирным закреплением концов (рис 1.4, в). Здесь реакции R1 , R2 и R3 направлены вдоль осей стержней.
4) Связь, осуществляемая точечной опорой (рис. 1.4 г). Реакция связей R1, R2 R3, направлены перпендикулярно поверхности опирающегося тела.
|
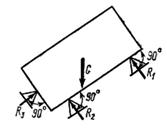
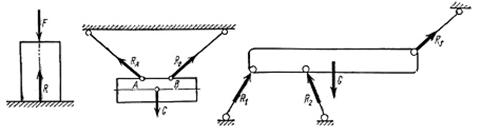
Рис. 1.4 Виды связей
Лекция № 2
ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
2.1 Геометрический метод сложения сил, приложенных в одной точке
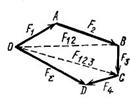
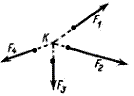
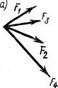
Линии действия сходящихся сил пересекаются в одной точке (рис. 2.1, а). Сходящиеся силы можно перенести в точку пересечения их линий действия (точка К, рис. 2.1, б).
|
Få = F1+F2+F3 +F4.
Рис. 2.1 Рис. 2.2
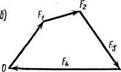
Для сложения векторов надо построить силовой многоугольник: в конец первого вектора помещаем начало второго, в конец второго – начало третьего и т. д. Для построения равнодействующей силы соединяем начало первого вектора с концом последнего.
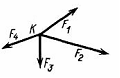
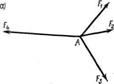
Геометрическое условие равновесия сходящихся сил – система сходящихся сил находится в равновесии, если Få = 0, т. е. при построении силового многоугольника конец последней слагаемой силы совместится с началом первой (рис. 2.2).
2.2 Проекция сил на ось
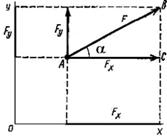
Fx - проекция вектора F на ось x - это отрезок, отсекаемый перпендикулярами, опущенными на ось х из начала и конца вектора F (рис. 2.3).
Fу - проекция вектора F на ось у - это отрезок, отсекаемый перпендикулярами, опущенными на ось у из начала и конца вектора F (рис. 2.4).
|
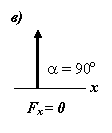
Fx = F cos a Fx = -F cos b
Рис. 2.3 Рис. 2.4
Значение проекции силы определяется из прямоугольного треугольника по правилу:
Катет прямоугольного треугольника равен гипотенузе, умноженной на
косинус прилежащего угла или на синус противолежащего угла.
Проекция вектора положительна (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора отрицательна (-), если направление от начала проекции к ее концу противоположно положительному направлению оси.
|
Задана система сходящихся сил F1, F2, F3, F4 (рис. 2.5, а). Построим силовой многоугольник и опустим из вершин силового многоугольника на ось х перпендикуляры (рис. 2.5, б).
|
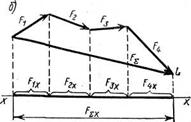
Få = F1+ F2+ F3+ F4
Рис. 2.5
Алгебраическое условие равновесия плоской системы сходящихся сил - система сходящихся сил находится в равновесии, когда алгебраические суммы проекций сил на каждую из двух координатных осей равны нулю:
ΣFix = 0
ΣFiy = 0
2.4 Определение реакций связи аналитическим методом
Пример (рис. 2.6, а). В точке В подвешены два груза - груз G1 = 600 Н и G2 = 400 Н. Определить реакции стержней АВ и ВС.
Этапы решения
1) Чертим расчетную схему (рис. 2.6, б). Для этого находим точку, где пересекаются линии действия всех сил. Это узел В. Прикладываем к нему на расчетной схеме внешние силы G1 и G2 (рис. 2.7, б).
2) Освобождаем выделенную точку от связей, а их действие заменяем реакциями. Связи в точке В осуществляются стержнями АВ и ВС. Прикладываем вместо них на расчетной схеме реакции стержней R1 и R2.
3) Выбираем координатные оси х и у (рис.2.6, б). Направление координатных осей х и у следует выбирать так, чтобы хотя бы одна из осей была перпендикулярна неизвестным силам (реакциям).
|
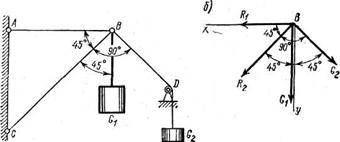
а) Схема нагружения б) Расчетная схема
Рис. 2.6
4) Составляем уравнения равновесия:
SFix = 0; R1 – G2 Cos45o + R2 Cos45o=0
SFiу = 0; G1 + R2 Cos45o + G2 Cos45o=0
5) Решаем уравнения: R2 = - G2 -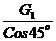 
= - 400 - 
= - 1249 Н.
R1 = G2 Cos45o - R2 Cos45o= 400 × 0,707 – (-1249)×0,707 = 1166 Н.
Знак минус перед значением реакции R2 показывает, что она направлена в противоположную сторону от выбранного направления.
Лекция № 3
ПАРА СИЛ И МОМЕНТЫ СИЛ
3.1 Пара сил
Пара сил – это две равные и параллельные силы, направленные в противоположные стороны и не лежащие на одной прямой. Пара сил, действующая на тело, стремится вращать это тело (рис. 3.1).
|
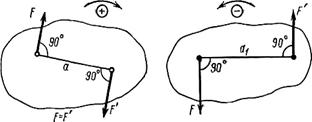
Рис. 3.1
Плечо пары (а) - кратчайшее расстояние между линиями действия сил (плечо всегда перпендикулярно силам).
Момент пары сил (М) - равен произведению одной из сил на ее плечо:
М = Fa = F'a, Н×м (3.1)
Момент пары сил положительный, если пара стремится повернуть тело по часовой стрелке (рис. 3.1, а), и отрицательным, если пара стремится вращать тело против часовой стрелки (рис. 3.1, б).
3.2 Сложение и равновесие пар сил на плоскости
Сложение пар производится алгебраическим суммированием их моментов:
М = М1 + М2 + …+ Мn = ΣМi
Условие равновесия системы пар, лежащих в одной плоскости: для равновесия системы пар необходимо чтобы сумма моментов пар равнялась нулю:
ΣМi = 0 (3.2)
Пример 3.1. Определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости (рис. 3.2). Первая пара F1 = F¢1 = 2 кН, плечо h1 = 1,25 м; вторая пара F2 = F¢2 = 3 кН, плечо h 2 = 2 м; третья пара F3 = F¢3 = 4,5 кН, плечо h3 = 1,2 м.
Рис. 3.2
3.3 Момент силы относительно точки
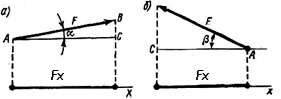
Момент Мо (F) силы F относительно точки О равен произведению силы на плечо. (рис. 3.3, а). Сила F стремится поворачивать плечо а вокруг точки О.
Мо (F) = F× a, Н×м, (3.3)
где а - плечо силы F.
Плечо силы – это длина перпендикуляра а, опущенного из точки на линию действия силы
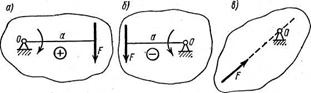
Рис. 3.3
Центр момента - точка О, относительно которой возникает момент.
Момент положительный, если сила стремится вращать тело по часовой стрелке (рис. 3.3, а), и отрицательный — против часовой стрелки (рис. 3.3, б).
Когда линия действия силы проходит через данную точку, момент силы относительно этой точки равен нулю, так как плечо а = 0 (рис. 3.3, в).
Лекция № 4
ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ
4.1 Опорные устройства балочных систем
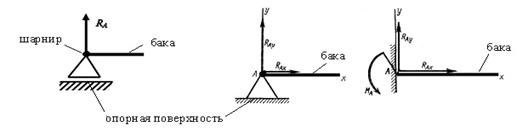
1) Шарнирно-подвижная опора (рис. 4.1, а)- допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Направление опорной реакции - перпендикуляр к опорной плоскости.
2) Шарнирно-неподвижная опора (рис, 4.1,б) - допускает только поворот вокруг оси шарнира, но не допускает никаких линейных перемещений. Опорная реакция RA раскладывается на две составляющие - RAx и RAy.
3) Жесткая заделка (защемление) (рис. 4.1,в)- не допускает ни линейных перемещений, ни поворота. В защемлении действуют две составляющие опорной реакции - RAx, RAy и реактивный момент МА.
а) б) в)
Рис. 4.1
Двухопорные балки имеют две опоры – одна опора шарнирно-неподвижная, вторая – шарнирно-подвижная. Шарнирно-подвижная опора необходима для компенсации перемещений балки при температурных расширениях балки из-за колебаний температуры, а также при возможной подвижке опоры, например, при осадке почвы.
4.2 Виды балок
Консоль – выступающая за опору не закрепленная часть балки (рис. 4.2, б, в).
1) Бесконсольные балки 2) Одноконсольные балки 3) Двухконсольные балки
|
а) б) в)
Рис. 4.2
4.3 Виды нагрузок
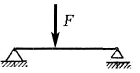
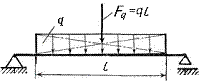
1) Сосредоточенная сила (рис.4.3, а) – F - сила, приложенная в одной точке.
а) б) в)
Рис. 4.3
2) Равномерно распределенная нагрузка (рис.4.3, б) – нагрузка, равномерно распределенная на некоторой длине l. Характеризуется интенсивностью q, единица измерения - Н/м или кН/м.
При решении задач равномерно распределенная нагрузка интенсивностью q заменяется одной силой Fq = q×l, которая является равнодействующей силой и прикладывается посередине длины l.
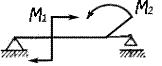
3) Пара сил или момент (рис. 4.3, в) – М, Н×м.
4.4 Равновесие плоской системы сил
Условие равновесия произвольной плоской системы сил - произвольная плоская система сил находится в равновесии, когда алгебраические суммы проекций сил на координатные оси и сумма моментов равны нулю:
Первый вид: Второй вид: Третий вид:
SFix = 0 S Fix = 0 SМА = 0
SFiу = 0 SМА = 0 SМВ = 0
SМо = 0 SМВ = 0 SМС = 0
4.5 Решение задач на определение опорных реакций
Для решения задач надо составить столько уравнений равновесия, сколько неизвестных сил в задаче. Для определения опорных реакций двухопорной балки (RAx, RAy и RВ) необходимо составить три уравнения равновесия второго вида: SFix = 0, SМА = 0, SМВ = 0.
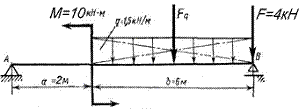
Пример 4.1. Определить опорные реакции балки, изображенной на рис. 4.4, а, нагруженной парой с моментом М = 10 кН×м, сосредоточенной силой F = 4 кН и распределенной нагрузкой интенсивностью q = 1,5 кН/м.
Решение.
1) Чертим расчетную схему (рис. 4.4, б). На расчетной схеме заменяем распределенную нагрузку q ее равнодействующей Fq = q×b, которая прикладывается посредине нагруженного участка b. Освобождаем балку от опор, а их действие заменяем реакциями - RAу, RAx и Rb. Проставляем расстояния между всеми силами и моментами – a, c, d, а также общую длину балки – l.
|
=
=4,62кН
|
|
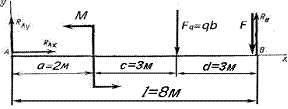
Рис. 4.4 Расчетная схема
4) Проверяем найденные значения реакций:
SFiv = 0; RAy - qb +RB - F = 4,63 – 1,5×6 + 8,37 - 4 = 0. Реакции найдены верно.
Лекция № 5
ЦЕНТР ТЯЖЕСТИ
5.1 Центр тяжести простых геометрических тел
Центр тяжести тела – это точка приложения силы тяжести
· Центр тяжести симметричной фигуры лежит на оси симметрии.
· Центр тяжести параллелограмма, прямоугольника, квадрата лежит в точке С пересечения диагоналей (рис. 5.1).
· Центр тяжести треугольника лежит на пересечении медиан (рис. 5.2).
·
|
|
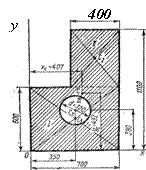
Рис. 5.1 Рис. 5.2 Рис. 5.3
Координаты центра тяжести плоских геометрических фигур определяют по формуле (5.1):
хс = 
; ус =
, (5.1)
где хс , ус – координаты центра тяжести всей фигуры;
хi , уi - координаты центра тяжести отдельных составных частей, из которых состоит фигура; Аi – площадь отдельных составных частей фигуры;
А – площадь всей фигуры.
Пример 5.1. Определить координаты центра тяжести плоской фигуры с круглым отверстием, изображенной на рис. 5.3.
Решение. Разбиваем фигуру на три части: два прямоугольника I и II и круглое отверстие III. Вычисляем координаты центров тяжести и площади этих частей:
х1 = 350 мм; у1 = 300 мм; А1 = 600×700 = 4200×102 мм2;
х2 = 500 мм; у2 = 850 мм; А2 = 400×500 = 2000×102 мм2;
х3 = 350 мм; у3= 380 мм; А3 = - 
- 
= - 804×102 мм2 (минус означает, что А3 – отверстие).
Вычисляем координаты центра тяжести всей фигуры:
xc =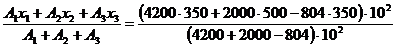
= 407 мм
ус =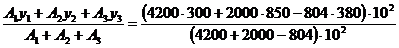
= 492 мм
5.3 Положение центров тяжести профилей проката
ГОСТ 8: ДВУТАВРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ
|
|
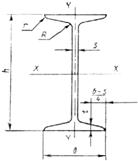
ГОСТ 8240-89 ШВЕЛЛЕРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ
|
|
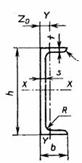
ГОСТ 8510 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ НЕРАВНОПОЛОЧНАЯ
|
|
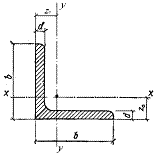
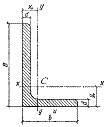
ГОСТ 8509 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ РАВНОПОЛОЧНАЯ
|
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Лекция № 6
ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
6.1 Основные понятия
Три основных вида расчетов - расчет на прочность, жесткость и устойчивость.
Прочность – это способность элементов конструкций, не разрушаясь, воспринимать действие различных нагрузок (например, растяжение, сжатие, изгиб и др.).
Жесткость – способность тела или конструкции сопротивляться деформации.
Деформация – это изменение формы и размеров элементов конструкций под действием внешних сил (виды деформации - растяжение, сжатие, изгиб, сдвиг, кручение).
Упругая деформация – деформация, которая полностью исчезает после снятия нагрузки.
Остаточная (пластическая) деформация – деформация, которая остается после снятия нагрузки (при проектировании размеры элементов конструкций назначают таким образом, чтобы возникновение остаточных деформаций было исключено).
Устойчивость – способность сооружения противостоять силам, стремящимся вывести его из равновесия.
6.2 Метод сечений
Метод сечений – Произведем мысленно поперечное сечение бруса (рис. 6.1) и одну часть бруса отбросим. Внешние силы, приложенные к оставленной левой части (F1, F2, F3) уравновешиваются внутренними силами, возникающими в плоскости сечения. Эти внутренние силы, возникающие в плоскости сечения, заменяют действие отброшенной части тела на оставленную часть.
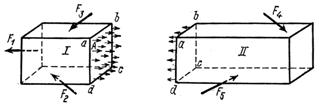
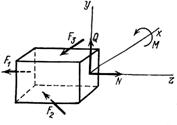
Рис. 6.1 Рис. 6.2
Направление координатных осей (рис. 6.2):
- ось z - вдоль оси стержня,
- оси х и у - вдоль главных центральных осей его поперечного сечения,
- начало координат в центре тяжести сечения.
Для любой части тела, I или II, в плоской системе сил можно составить три уравнения равновесия:
S Fiу = 0,
S Fiz = 0,
S Мix = 0 (6.1)
Внутренние силовые факторы при действии на стержень плоской системы сил (рис. 6.2):
N - продольная сила;
Q - поперечная сила;
М - изгибающий момент.
6.3 Виды деформаций
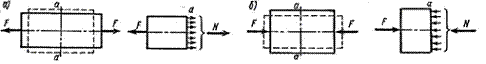
Рис. 6.3
Растяжение – в сечении возникает продольная сила - N, направленная наружу (рис. 6.3, а).
Сжатие - в сечении возникает продольная сила – N, направленная внутрь (рис. 6.3, б).
Сдвиг (рис. 6.4) - в сечении возникает поперечная сила - Q.
Кручение (рис. 6.5) - в сечении возникает крутящий момент - Мк
Изгиб – в сечении возникают изгибающий момент – М и поперечная сила - Q.
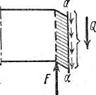
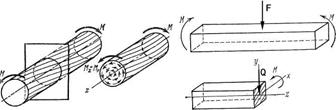
Рис. 6.4 Рис. 6.5 Рис. 6.6
6.4 Напряжения
Напряжение (r) - это значение внутренних сил, приходящихся на единицу площади сечения.
|
r = F/А, МПа
где А – площадь сечения бруса (рис. 6.7);
F – сила, действующая на сечение А (рис.6.7);
1 МПа = 1 Н/мм2
|
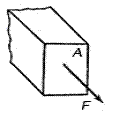
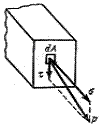
Рис. 6.7 Рис. 6.8
Предельное напряжение (sпред, tпред) – это напряжение, при котором происходит разрушение материала.
Допускаемое напряжение ([s], [t]) - это максимальное напряжение, обеспечивающее безопасную работу материала. Определены путем проведения испытаний образцов материалов и занесены в справочные таблицы.
[s] = sпред / [n]; [t] = tпред / [n]
Коэффициент запаса прочности [n] — показывает, во сколько раз допускаемое напряжение должно быть меньше предельного (зависит от свойств материала, характера действующих нагрузок и условий работы элемента конструкции).
Лекция № 7
РАСТЯЖЕНИЕ И СЖАТИЕ
7.1 Расчеты на прочность при растяжении и сжатии
Условие прочности при осевом растяжении и сжатии:
s = N/A £ [s], (7.1)
где N - значение продольной силы в сечении;
А - площадь поперечного сечения;
[s] - допускаемое напряжение при растяжении или сжатии для материала стержня.
Допускаемое напряжение [s] устанавливается на основе результатов механических испытаний образцов материалов и заносится в справочные таблицы (см. табл. 7.1).
Таблица 7.1 - Допускаемые напряжения для некоторых материалов
Материал | Допускаемые напряжения | |
при растяжении [sр ], МПа | при сжатии [sс ], МПа | |
Сталь Ст3 | ||
Сталь 45 | ||
Древесина вдоль волокон | 10 - 15 | 10 - 12 |
Три вида задач при расчете на прочность:
1) Проверка прочности (проверочный расчет). При заданных продольной силе N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым по формуле (7.1).
s = N/A £ [s]
2) Подбор сечения (проектный расчет). Определяют необходимые размеры сечения, зная продольную силу и допускаемое напряжение:
A ³ N / [s] (7.2)
3) Определение допускаемой продольной силы:
[N] < [s]× А (7.3)
7.2 Эпюры продольных сил и нормальных напряжений при растяжении и сжатии
Эпюра - это диаграмма, показывающая изменение продольной силы (N ) или напряжения (s) по длине стержня (рис. 7.1, в). Если продольные силы или напряжения одинаковы во всех сечениях, эпюра изображается прямоугольником.
|
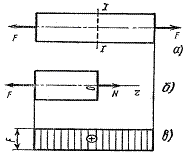
Рис. 7.1
Для построения эпюр необходимо рассчитать продольные силы и нормальные напряжения, используя метод сечений. Брус делят на участки. Границами участков являются точки приложения внешних сил и места изменения размеров поперечного сечения.
Значение продольной силы не зависит от того, какую из отсеченных частей рассматривать, но целесообразнее рассматривать ту часть стержня, к которой приложено меньше сил.
Пример. Для заданного ступенчатого бруса, изготовленного из стали марки Ст3 (рис. 7.2, а) построить эпюры продольных сил и нормальных напряжений; проверить брус на прочность. Допускаемое напряжение для материала бруса согласно табл. 7.1 [s] = 160 МПа.
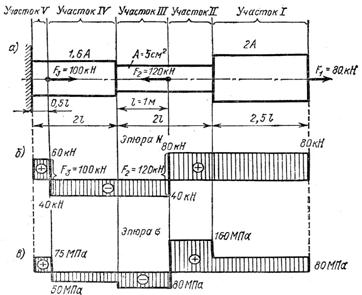
Рис. 7.2
Решение.
1) Разобьем брус на 5 участков, начиная от свободного конца. Границы участков определяются точками приложения внешних сил или местами изменения размеров поперечного сечения. Проводим сечения на каждом участке, отбрасываем часть бруса со стороны заделки (левую), определяем продольные силы:
2) Положительным направлением оси z считается в сторону от заделки бруса в стену. То есть, все растягивающие брус силы – положительны, а сжимающие силы – отрицательны. Составляем уравнения равновесия ΣFZ = 0:
Первый участок: F1 - N1 = 0, N1 = F1 = 80 кН (брус растянут).
Второй участок: F1 - N2 = 0, N2 = F1 = 80 кН (брус растянут).
Третий участок: F1 – F2 - N3 = 0, N3 = F1 – F2 == - 40 кН (брус сжат).
Четвертый участок: F1 – F2 - N4 = 0, N4 = F1 – F2 == - 40 кН (брус сжат).
Пятый участок: F1 - F2 + F3 - N5= 0, N5 = F1 - F2 + F3 =+ 100 = 60 кН (брус растянут).
Эпюра нормальных продольных сил (N) построена на рис. 7.2, б.
Определяем напряжения:
Первый участок (площадь сечения А1 = 2А = 1000 мм2 = 10-3 м2)
s1 = N1 /A1 = 80 000/10 -3 = 80×106 Па = 80 МПа.
Второй участок (А2 = А = 500 мм2 = 0,5×10-3 м2)
s2 = N2 /A2 =/(0,5×10-3) = 160×106 Па = 160 МПа.
Третий участок ( А3 = А = 500 мм2 = 0,5×10 -3 м2)
s3 = N3 /A3 = - 40 000/(0,5×10-3 ) = - 80×106 Па = - 80 МПа.
Четвертый участок (А4= 1,6А = 800 мм2 = 0,8× 10-3 м2)
s4 = N4 /A4 = - 40000/(0,8×10 -3) = - 50×106 Па = - 50 МПа.
Пятый участок (А5 = 1,6А = 800 мм2 = 0,8×10-3 м2)
s5 = N5 /A5 =/(0,8×= 75×106 Па = 75 МПа.
Эпюра нормальных напряжений построена на рис. 7.2, в. Наибольшее рабочее напряжение возникает в пределах второго участка smax = 160 МПа. Сравнив его с допускаемым напряжением, обнаруживаем, что они равны и прочность бруса гарантирована.
Лекция № 8
ДЕФОРМАЦИЯ ПРИ УПРУГОМ РАСТЯЖЕНИИ И СЖАТИИ
8.1 Продольная и поперечная деформация при растяжении
При растяжении стержня его первоначальная длина равна l (рис. 8.1), а длина после растяжения l1.. Поперечный размер, первоначально равный а, (рис. 8.1) уменьшается до а1.
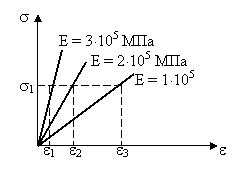
Рис. 8.1
Рис. 8.2
Удлинение стержня Dl = l1 - l
Изменение поперечного размера Dа = а – а1,
Продольная деформация - e = 
- безразмерная или e = ×100% (в процентах)
Поперечная деформация: - e^ = 
- безразмерная или e^ = ×100% (в процентах)
Коэффициент Пуассона - m = | e^/ e |
Закон Гука – продольная деформация e прямо пропорциональна соответствующему нормальному напряжению s:
|
Е, МПа - модуль продольной упругости - характеризует жесткость материала, т. е. способность материала сопротивляться упругому деформированию. Чем больше модуль продольной упругости материала (Е), тем круче график зависимости деформации от напряжения (рис. 8.2). Чем больше Е, тем меньше при одном и том же напряжении (s1) значение деформации(e1< e2< e3), а чем меньше деформация, тем материал более жесткий.
m и Е - величины постоянные для данного материала при упругом растяжении (сжатии).
8.2 Виды механических испытаний материалов
По характеру приложения внешних сил:
- статические испытания – испытания медленно изменяющейся нагрузкой;
- динамические испытания - испытания ударной нагрузкой;
- испытания на выносливость – испытания переменной нагрузкой.
По видам деформации - испытания на растяжение, сжатие, изгиб, срез, кручение.
8.3 Диаграмма растяжения (сжатия)
Диаграмма растяжения строится в координатах s, e (рис. 8.3) и не зависит от геометрических размеров испытываемого образца.
|
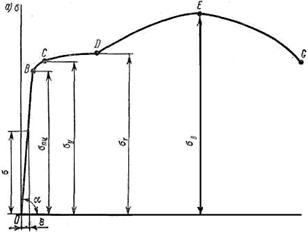
Рис. 8.3 – Диаграмма растяжения
Участок ОВ - линейная зависимость (прямая пропорциональность) между величинами относительного удлинения e и напряжения s, т. е. соблюдается закон Гука. Угол наклона пропорционален модулю продольной упругости материала - tg а = s/e = Е. Чем круче этот участок, тем больше модуль упругости материала, тем он жестче.
Точка В - предел пропорциональности - sпц.
Участок ВС - закон Гука нарушается: удлинение растет интенсивнее, чем сила. До точки С увеличение растягивающей силы практически не вызывает остаточных деформаций образца. Материал деформируется упруго.
Точка С - предел упругости - sу (предел пропорциональности sпц и предел упругости sу для многих материалов, например для стали, оказываются настолько близки, что зачастую их считают совпадающими и отождествляют несмотря на физическое различие этих пределов).
Участок CD – почти прямой, что указывает на значительное возрастание удлинения при постоянном значении силы; материал, как говорят, течет.
Точка D - sт, - предел текучести. При этом напряжении происходит значительный рост пластической (остаточной) деформации. Предел текучести является характеристикой прочности при растяжении пластичных материалов (например, малоуглеродистая сталь), так как появление больших остаточных деформаций является нарушением прочности конструкции.
Участок DE - зоной упрочнения - материал вновь начинает сопротивляться росту деформаций, но зависимость между деформацией и напряжением уже не подчиняется закону Гука. Кроме упругого удлинения образец получает значительное остаточное удлинение.
Точка Е - временное сопротивление sв. (максимальная растягивающая сила), На образце при этом значении силы образуется резкое, местное сужение - шейка.
Участок EG - образец сильно удлиняется за счет пластической деформации шейки.
Точка G - разрушение образца.
Лекция № 9
РАСЧЕТЫ НА СРЕЗ И СМЯТИЕ
9.1 Срез
|
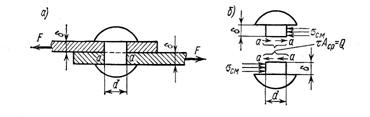
Рис. 9.1
Условие прочности элементов, работающих на срез:
t = Q/Aср £ [t ср], (9.1)
где t - касательные напряжения, возникающие при срезе;
[tср] - допускаемое касательное напряжение (назначают на основании испытаний на срез);
Q - поперечная сила возникающая в сечении аа;
Аср - площадь среза (например, для заклепки площадь среза равна площади ее поперечного
сечения Аср = pd2 /4).
9.2 Смятие
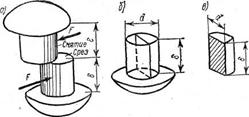
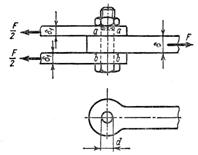
Рис. 9.2 Рис. 9.3
Смятие - это местная деформация сжатия по отдельным площадкам.
Площадка смятия у заклепки - боковая поверхность полуцилиндра высотой, равной толщине листа d (рис. 9.2, а, б).
Условие прочности элементов, работающих на смятие:
sсм = Q /Асм £ [sсм] (9.2)
где Асм - площадь смятия (например, для заклепки равна площади продольного сечения стержня,
то есть прямоугольник Асм = d×d (рис. 9.2, б, в);
[sсм] - допускаемое напряжение на смятие.
Пример/ Определить, исходя из условий прочности на срез и смятие, необходимый диаметр болта (рис. 13.3) d = 20 мм; d1 = 12 мм; [tср] = 100 Н/мм2; [sсм] = 240 Н/мм2, F = 120 кН.
Решение
1) Расчет на срез. Так как болт работает на срез одновременно по двум сечениям - аа и бб, то площадь среза:
Аср =2 pd2 /4 = pd2 /2
Из условия прочности на срез:
t = F/Aср £ [t ср] ® Аср = pd2 /2 ³ F / [t ср] ® d ³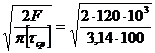 
= 27,6 мм
2) Расчет на смятие. Так как 2d1 = 24 > d = 20, то опасной в отношении смятия является внутренняя деталь толщиной d. Площадь ее смятия Асм = d×d. Из условия прочности на смятие:
sсм = F /Асм £ [sсм] ® Асм = d×d ³ F /[sсм] ® d ³ 
= 25 мм
Из двух значений диаметра d, рассчитанных из условий прочности на срез и смятие, следует принять большее, т. е. d ³ 27,6 мм. По ГОСТ это болт с диаметром ненарезанной части 28 мм и резьбой М27.
Лекция № 10
ИЗГИБ
10.1 Основные понятия
Прямой изгиб – это искривление продольной оси балки, при котором внешние силы перпендикулярны к продольной оси и расположены в одной плоскости (рис. 10.1, а). Встречается чаще всего.
Косой изгиб – изгиб балки, при котором внешние силы не перпендикулярны к оси балки (рис. 10.1, б).
Два внутренних силовых фактора в поперечных сечениях балок при изгибе:
- изгибающий момент – М;
- поперечная сила – Q.
Чистый изгиб - в поперечных сечениях балки возникает только изгибающий момент (М), а поперечная сила равна нулю. Балка изгибается двумя противоположно направленными парами сил, приложенными к ее торцам (рис. 10.1, в).
Рис. 10.1
10.2 Поперечные силы и изгибающие моменты в сечениях балок
На балку АВ (рис. 10.2, а), действуют силы F1, F2, F3. Опорные реакции RA и RB определяют из уравнений равновесия. Проведем мысленно поперечное сечение С. (рис. 10.2, б и в). Внутренние силы в любом сечении балки могут быть заменены поперечной силой - Q и изгибающим моментом – М. Левая часть находится в равновесии под действием внешних сил RA, F1, F2 и внутренних сил, возникающих в сечении С, – М и Q. Правая часть находится в равновесии под действием внешних сил F3, RB и внутренних сил в сечении С, - М и Q. Согласно закону равенства действия и противодействия, внутренние силы по сечению С для левой и правой частей одинаковы, но направлены в противоположные стороны.
|
| ||
|
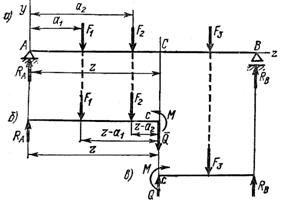
Рис. 10.2 Рис. 10.3 – Правило знаков
Поперечная сила (Q) в каком-либо поперечном сечении балки равна алгебраической сумме проекций на ось у внешних сил, действующих на балку по одну сторону от рассматриваемого сечения.
Изгибающий момент (М) равен алгебраической сумме моментов сил относительно центра тяжести сечения по одну сторону.
С учетом правила знаков для изгибающих моментов и поперечных сил, показанных на рисунке 10.3, получим: Q = Ra – F1 - F2; М = RAz – F1 (z – а1) – F2 (z – а2).
Лекция № 11
ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
Эпюра поперечных сил – это график, показывающий изменение поперечных сил по длине балки
Эпюра изгибающих моментов – это график, показывающий изменение изгибающих моментов по длине балки.
11.1 Эпюры Q и М при различных видах нагружения
· Балка с защемленным концом, нагруженная на свободном конце парой сил с моментом М (рис. 11.1, а). Поперечная сила равна нулю (Q = 0). Изгибающий момент в любом сечении равен внешнему моменту – М. Он положителен, так как слева от сечения балка изгибается выпуклостью вниз (см. рис. 10.3 – Правило знаков).
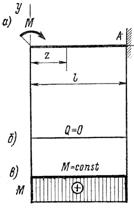
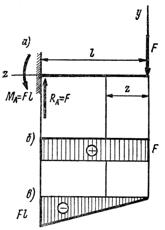
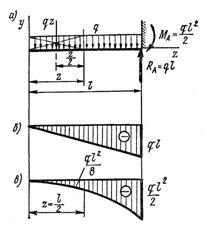
Рис. 11.1 Рис. 11.2 Рис. 11.3
· Балка с защемленным концом, нагруженной силой на свободном конце (рис. 11.2, а). Проведем сечение, отбросим заделку и рассмотрим равновесие правой части балки. В любом сечении z поперечная сила равна силе F и положительна. Эпюра поперечных сил (рис. 11.2, б) ограничивается прямой, параллельной оси балки. Изгибающий момент в сечении z равен М = - Fz (он отрицателен, так как сила F изгибает балку выпуклостью вверх). Эпюра изгибающих моментов изображается треугольником (рис. 11.2, в). В сечении заделки М = - Fl.
· Балка с защемленным концом, к которой приложена равномерно распределенная нагрузка (рис. 11.3, а). Вся нагрузка, действующая на балку, равна ql. Отбросим заделку и рассмотрим равновесие левой части. В сечении z поперечная сила Q = - qz. Эпюра поперечных сил (рис. 11.3, б) - треугольник: при z = 0, Q = 0; при z = l (в защемлении) Q = - ql.
В сечении z изгибающий момент М = - qz× (z/2) = - qz2 /2, где z/2 – плечо.
Эпюра изгибающих моментов - парабола так как z2 - в квадрате (рис. 11.3, в). Можно построить ее по точкам: при z = 0, М = 0,
при z = l/2, М = - (ql2/8),
при z = l, М = -(ql2/ 2).
· Двухопорная балка, нагруженная сосредоточенной силой (рис. 11.4, а)
|
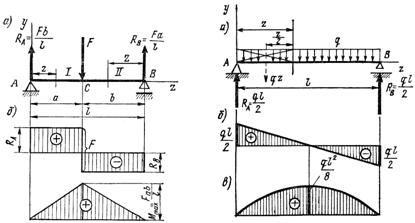
Рис. 11.4 Рис. 11.5
Разделим балку на два участка: АС и СВ, их границей является точка приложения силы F.
Эпюра поперечных сил (рис. 11.4, б): в любом сечении на первом участке Q1 = RA, на втором участке Q2 = - RВ (отрицательна, т. к. реакция RВ справа от сечения направлена вверх). В точке приложения силы F эпюра делает скачек на величину этой силы.
Эпюра изгибающих моментов (рис. 11.4, в)
На участке I М1 = RA z. Эпюра – прямая линия, которую можно построить по двум точкам: при z = 0, т. е. в сечении на левой опоре, М1 = RA ×0 = 0 и при z = а, М1 = RА×а = Fba/l.
На участке II М2 = RВ z. При z = b, т. Е. в сечении под силой F, М2 = RВ ×b = Fab/l; при z = 0, т. е. в сечении на правой опоре, М2 = RВ ×0 = 0.
·Двухопорная балка, к которой приложена равномерно распределенная нагрузка (рис.11.5, а)
Определим опорные реакции: Ra = RB = ql/2.
Эпюра поперечных сил (рис. 11.5, б):
в произвольном сечении z, для левой отсеченной части: Q = Ra - qz = ql/2 – qz;
при z = 0 Q = ql/2;
при z = l/2 Q = 0;
при z = l Q = - ql/2.
Эпюра изгибающих моментов (рис. 11.5, в): М = RAz - qz (z/2) = (ql/2) z - gz2/2;
при z = 0 M = 0;
при z = l/2 M = ql2/8;
при z = l M = 0.
В это уравнение z входит во второй степени, поэтому эпюра М имеет вид параболы. Посередине балки поперечная сила изменяет знак, а изгибающий момент максимален: Мmax = ql2/8.
11.2 Характерные точки на эпюрах Q и М
1) При любом виде нагружения двухопорной балки, если в опорах не приложены внешние силы F, то (рис. 11.6):
- на левой опоре (опора А) QА = RА,
- на правой опоре (опора В) QВ = - RВ.
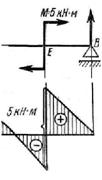
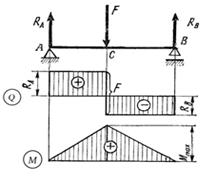
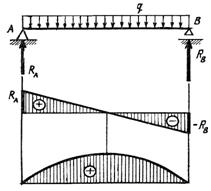
Рис. 11.6 Рис. 11.7 Рис. 11.8
2) Если на левую опору действует внешняя сила F, то:
ü внешняя сила F направлена вниз: QА = RА – F,
ü внешняя сила F направлена вверх: QА = RА + F.
3) Если на правую опору действует внешняя сила F, то:
ü внешняя сила F направлена вниз: QВ = - RВ + F;
ü внешняя сила F направлена вверх: QВ = - RВ – F.
4) На участках, где нет равномерно распределенной нагрузки (рис. 11.6):
ü эпюра Q – прямоугольная;
ü эпюра М – треугольная.
5) В точках приложения сосредоточенных сил F (рис. 11.6):
ü на эпюре Q - скачки, равные по величине этим силам F,
ü на эпюре М - переломы, направленные навстречу силам F.
6) На участках, загруженных равномерно-распределенной нагрузкой, (рис. 11.7):
ü эпюра Q - треугольная,
ü эпюра М – парабола, выпуклость которой направлена навстречу нагрузке
7) В точках, где Q = 0, эпюра М принимает максимальное или минимальное значение (рис. 11.7).
8) Если в опорах А и В двухопорной бесконсольной балки не приложен момент, то на эпюре М:
ü МА = 0, МВ = 0 (рис. 11.6, 11.7).
9) В точках приложения моментов (пар сил) на эпюре М - скачки, равные величине моментов (рис. 11.8).
11.3 Порядок построения эпюр
1) Составляем уравнения равновесия и определяем опорные реакции - Ra и RB
2) Разбиваем балку на участки. Обозначаем буквами границы участков: точки приложения опорных реакций – А, В; точки приложения внешних сил (F) и моментов (М) начало и конец равномерно-распределенной нагрузки - С, D, E, G … (рис. 11.9).
3) Проводим сечения на границе каждого участка. Отбрасываем ту часть балки, к которой приложено больше сил. Для оставшейся части составляем уравнения равновесия для поперечных сил Q = SFлев или Q = SFправ с учетом правила знаков. Определяем на каждом участке поперечную силу - QА, QВ, QО, QE и т. д. В точках приложения внешних сил F сечение проводим слева и справа от этих точек (например, рис. 11.9 - 
, 
).
4) Выбираем масштаб для поперечных сил и строим эпюру Q.
5) Составляем уравнения равновесия для изгибающих моментов с учетом правила знаков и определяем моменты на каждом участке - МА, МВ, МО, МD и т. д. В точках приложения внешних моментов (М) сечение проводим слева и справа от этих точек (например, рис. 11.9 - 
, 
)
6) На участке с равномерно распределенной нагрузкой из подобия треугольников на эпюре Q определяем положение точки, в которой Q = 0 (точки С). На эпюре М в этой точке будет вершина параболы.
7) Определяем изгибающий момент в точке вершины параболы.
8) Выбираем масштаб для изгибающих моментов и строим эпюру М.
Примечание: Для балок с защемленным концом определять реакции заделки не обязательно. уравнения составляют для той части балки, к которой приложены только внешние силы (т. е. защемленный конец отбрасывают).
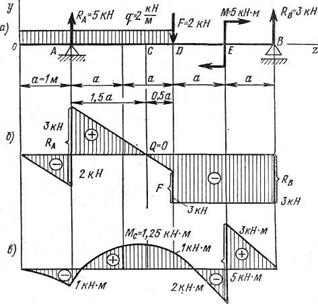Пример. Построить эпюры поперечных сил и изгибающих моментов для балки на рис. 11.9.
Решение. Определяем опорные реакции:
SМА = 0 q×3a×0,5а + F×2a + M - RB×4a = 2×3×0,5 + 2×2 + 5 - RB×4 = 0. Откуда RB = 12/4 = 3 kH;
SМВ = 0 - q×3a×3,5а + RА×4a - F×2a + М = 2×3×3,5 + RА×4 - 2×2 + 5 = 0. Откуда Ra = 20/4 = 5 кН.
Разбиваем балку на участки. Характерные точки - А, В, D, Е.
Построение эпюры поперечных сил (Q)
(рис. 11.9, б).
Вычисляем значения поперечных сил:
|
В сечении А слева QАлев = - qa = -2 кН.
На участке ОА эпюра поперечных сил ограничена наклонной прямой.
|
В сечении А справа QAправ = - qa + RA = - 2 + 5 = 3 кН; здесь имеет место скачок, равный RA = 5 кН.
В сечении D слева QDлев = - 3qa +RA = -3×2+5 = -1 кН.
В сечении D справа QDправ = - 3qa + RA - F = - 3× 2 + 5 - 2 = - 3 кН. В сечении D эпюра Q имеет место скачок, равный величине приложенной силы F = 2 кН.
|
В точке С поперечная сила Q = 0. Здесь изгибающий момент должен принять максимальное значение. Из подобия треугольных элементов эпюры на участке AD определяем, что точка С лежит на расстоянии 1,5а от опоры А или 0,5а от сечения D.
В сечении В слева QВлев = RA – F – q ×3 = 5 – 2 - 2×3 = - 3 кН
Построение эпюры изгибающих моментов (рис. 11.9, в).
В сечении О М = 0.
В сечении А МА = - qа2/2 = - 2× 12/2 = -1 кН×м; на консоли эпюра моментов изображается параболой как на участке, загруженном равномерно-распределенной нагрузкой,
В сечении С Мс = -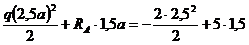
= 1,25 кН×м. Это значение момента является максимальным на участке AD (вершина параболы).
В сечении D MD = - q×3a× 1,5a +RA×2a = -2×3×1,5 + 5×2 = 1кНм.
В сечении Е слева МЕлев = - q×3a×2,5a + RA ×За - Fa= -2× 3×2,5+ 5×3 - 2×1 = - 2 кН×м.
В сечении Е справа МЕправ = МЕлев + М = - 2+5 = 3 кН×м.
В сечении В Мв = 0. На участках DE и ЕВ, свободных от распределенной нагрузки, эпюра моментов ограничена прямыми наклонными линиями; в сечении Е имеет место скачок на величину приложенной пары М = 5 кНм.
Лекция № 12
РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
12.1 Нормальные напряжения при изгибе
При изгибе продольные волокна балки на выпуклой стороне удлиняются, а на вогнутой укорачиваются (рис.12.1). Слой волокон, лежащих на половине высоты балки, сохраняет, искривившись, неизменную длину. (рис. 12.2).
Нейтральный слой - это слой, длина которого не изменяется при изгибе и не испытывает напряжений.
|
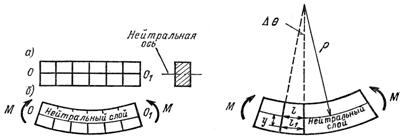
Рис. 12.1 Рис. 12.2
Удлинение волокна: Dl = l1 - l,
Относительное удлинение (продольная деформация): e =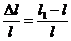 
При изгибе в сечениях балки от действия изгибающих моментов возникают нормальные напряжения (s), а от поперечных сил Q - касательные напряжения (t). Но в большинстве случаев касательные напряжения невелики и при расчетах на прочность не учитываются.
12.2 Осевой момент сопротивления
Осевой момент сопротивления (Wx, см3) - характеризует способность сечения балки сопротивляться изгибу и зависит от формы поперечного сечения балки.
Для профилей проката (уголков, швеллеров, двутавров и др.) осевой момент сопротивления определяется по таблице сортамента (пример – в таблице 12.1)
Таблица 12.1
ГОСТ 8239-89: Двутавры стальные горячекатаные | |||||||||||||||
Номер двутавра
| Размеры | Площадь | Масса | Справочные значения для осей | |||||||||||
h | b | s | t | R | r | X – X | Y – Y | ||||||||
не более мм | Ix, | Wx, | ix, | Sx, | Iy, | Wy, | iy, | ||||||||
см2 | см4 | см3 | см | см3 | см4 | см3 | См | ||||||||
10 | 100 | 55 | 4,5 | 7,2 | 7,0 | 2,5 | 12,0 | 9,46 | 198 | 39,7 | 4,06 | 23,0 | 17,9 | 6,49 | 1,22 |
12 | 120 | 64 | 4,8 | 7,3 | 7,5 | 3,0 | 14,7 | 11,50 | 350 | 58,4 | 4,88 | 33,7 | 27,9 | 8,72 | 1,38 |
14 | 140 | 73 | 4,9 | 7,5 | 8,0 | 3,0 | 17,4 | 13,70 | 572 | 81,7 | 5,73 | 46,8 | 41,9 | 11,50 | 1,55 |
16 | 160 | 81 | 5,0 | 7,8 | 8,5 | 3,5 | 20,2 | 15,90 | 873 | 109,0 | 6,57 | 62,3 | 58,6 | 14,50 | 1,70 |
18 | 180 | 90 | 5,1 | 8,1 | 9,0 | 3,5 | 23,4 | 18,40 | 1290 | 143,0 | 7,42 | 81,4 | 82,6 | 18,40 | 1,88 |
20 | 200 | 100 | 5,2 | 8,4 | 9,5 | 4,0 | 26,8 | 21,00 | 1840 | 184,0 | 8,28 | 104,0 | 115,0 | 23,10 | 2,07 |
22 | 220 | 110 | 5,4 | 8,7 | 10,0 | 4,0 | 30,6 | 24,00 | 2550 | 232,0 | 9,13 | 131,0 | 157,0 | 28,60 | 2,27 |
12.4 Три вида расчета на прочность при изгибе
1) Проверка прочности (проверочный расчет) - производится в том случае, когда известны размеры сечения балки, наибольший изгибающий момент и допускаемые напряжения: наибольшие нормальные напряжения в поперечных сечениях не должны превосходить допускаемых напряжений на растяжение или сжатие.
| s |max = | M |max /Wx £ [s], где (12.1)
2) Подбор сечения (проектный расчет) производится в том случае, когда заданы действующие на балку нагрузки, т. е. можно определить наибольший изгибающий момент | М |mах и допускаемое напряжение [s]:
Wx ³ | M |max / [s] (12.2)
По необходимому моменту сопротивления Wx, задавшись формой сечения, подбирают его размеры.
3) Определение наибольшего допускаемого изгибающего момента производится в том случае, когда заданы размеры сечения балки и допускаемое напряжение:
| M |max £ Wx [s] (12.3)
Наиболее выгодны такие формы сечений, которые дают наибольший момент сопротивления при наименьшей площади. Такому условию в первую очередь удовлетворяет двутавровое сечение, у которого почти весь материал отнесен от нейтральной оси к верхней и нижней полкам, что увеличивает момент сопротивления Wx. Менее выгодно прямоугольное сечение; круглое сечение еще менее выгодно. Полые сечения всегда выгоднее сплошных сечений. Целесообразно применять сечения балок из прокатных профилей: двутавров, швеллеров и т. п. В сортаменте для этих профилей приводятся числовые значения всех необходимых геометрических характеристик.
Пример. Наибольший изгибающий момент в поперечном сечении балки Mmax = 37,5 кН×м. Подобрать сечение стальной балки из двутавра. Допускаемое напряжение [s] = 160 Н/мм3 .
Решение. Требуемый момент сопротивления:
Wx ³ | M |max / [s] = 37,5 ×106 / 160 = 234 ×103 мм3 =234 см3.
Подбираем сечение балки в трех вариантах.
1) Двутавр. По таблице ГОСТ 8239—72 подходит двутавровый профиль № 22а. Его момент сопротивления Wx = 254 см3.
Лекция № 13
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
13.1 Понятие о продольном изгибе
Продольный изгиб (рис. 13.1) – происходит при увеличении сжимающих продольных сил выше критического значения, при котором ось стержня искривляется.
Критическая сила FKP - максимальная сжимающая продольная сила, при которой прямолинейная форма стержня является устойчивой.
При сжимающей силе меньше критической стержень работает на сжатие; при силе, равной критической, стержень работает на сжатие и изгиб.
Даже при небольшом превышении сжимающей нагрузкой критического значения прогибы стержня нарастают чрезвычайно быстро, и стержень получает недопустимо большие деформации, приводящие к разрушению конструкции. Поэтому критическая сила должна рассматриваться как разрушающая нагрузка.
Допускаемая сжимающая сила [F ] должна быть в несколько раз меньше критической:
[F] = FKP /[ny],
где [F ] - допускаемое значение силы, сжимающей стержень;
Fкр - критическое значение сжимающей силы для рассчитываемого стержня;
[nу] - нормативный коэффициент запаса устойчивости.
Критическая сила зависит от способов закрепления концов стержня.
Основной случай продольного изгиба - шарнирное закрепление обоих концов стержня (рис. 13.1).
Формула Эйлера для стержня с шарнирно-закрепленными концами:
Fкр = 
Jmin – минимальное значение момента инерции поперечного сечения стержня (при потере устойчивости стержень изгибается в плоскости наименьшей жесткости, т. е. каждое из его поперечных сечений поворачивается вокруг той из главных осей, относительно которой момент инерции минимален)
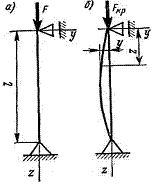
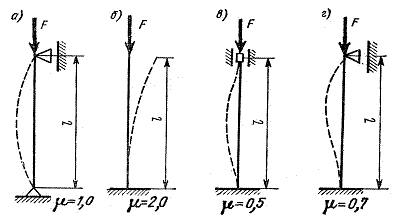
Рис. 13.1 Рис. 13.2
Приведенная длина стержня lпр - длина стержня при различных способах закрепления его канцов, приведенная к длине стержня, закрепленного с обоих концов шарнирами.
lпр = ml
m - коэффициент приведения длины (рис. 13.2) – показывает во сколько раз следует увеличить длину стержня, закрепленного с обеих концов шарнирами, чтобы критическая сила для него была равна критической силе в данных условиях закрепления
Формула Эйлера при любом способе закрепления стержня:
Fкр = 
Критическое напряжение sкр - нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы.
sкр =
= 
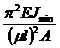
Jmin /А = i2min - отношение момента инерции к площади равно квадрату радиуса инерции:
imin = 
- минимальный радиус инерции сечения.
Гибкость стержня (l) - безразмерная величина, равная отношению: l = ml/ imin, откуда:
sкр = 
Чем больше гибкость l, тем меньше критическое напряжение, тем меньше критическая сила, которая вызовет продольный изгиб стержня:
13.2 Предел применимости формулы Эйлера
Формула Эйлера справедлива лишь при больших гибкостях, превышающих некоторое предельное значение lпред, при котором напряжения в стержне достигнут предела пропорциональности sпц:
sкр = 
sпц, откуда lпред = 
Формула Эйлера справедлива при гибкостях более:
- для стержней из малоуглеродистой стали lпред = 100,
- для деревянных стержней lпред = 75,
- для чугунных стержней lпред = 80.
На практике приходится иметь дело со сжатыми стержнями, гибкость которых меньше предельной. В таких случаях формулу Эйлера использовать нельзя.
Когда формула Эйлера оказывается неприменимой, пользуются эмпирическими формулами для вычисления критического напряжения в стальных стержнях:
sкр = а - bl
где а и b - коэффициенты, характеризующие качество материала. Значения этих коэффициентов приводятся в технических справочниках.
Для стали марки СтЗ при гибкости 60 < l < 100 формула имеет вид:
sкр = (304 – 11,2l), Н/мм2
Для стальных стержней малой гибкости при l< 60 опасна не потеря устойчивости, а появление значительных остаточных деформаций. В этом случае под критическим напряжением следует понимать предел текучести, т. е. sкр = sт;
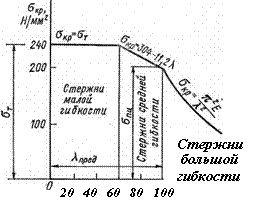На рис. 13.3 приведен график, характеризующий зависимость критического напряжения от гибкости для стержней из стали СтЗ.
Стержни большой гибкости - стержни, для которых справедлива формула ЭйЛера.
Стержнями средней гибкости - стержни, для которых справедлива формула .
Стержни малой гибкости – стержни, для которых критические напряжения, вычисленные по формуле Ясинского, превышают предел текучести. Для них критические напряжения также приравнивают пределу текучести.
|
[F] = sKP А/[ny]
Пример 13.1. Определить допускаемую величину сжимающей силы для чугунной колонны длиной l = 3 м с одним защемленным концом, а другим — свободным. Сечение колонны — кольцо, наружный диаметр dН = 200 мм, внутренний dB = 160 мм. Модуль продольной упругости для чугуна Е = 105 Н/мм2, требуемый коэффициент запаса устойчивости [nу] = 5.
Решение.
1) Вычислим осевой момент инерции поперечного сечения колонны
J » 0,05dн4 (1 - a4) = 4700 ×104 мм4, где a= dB/dн = 160/200 = 0,8.
2) Площадь сечения колонны А = p/4(dн2 + dВ2) = 113 ×102 мм2.
3) Радиус инерции сечения i =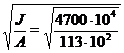 
= 64,2 мм
4) Расчетная длина колонны при m = 2 (см. рис. 24.2, б) ml = 2 ×3000 = 6000 мм.
5) Гибкость колонны l = ml/ i = 6000/64,2 = 93,5 > l пред
Следовательно, расчет данной колонны можно вести по формуле Эйлера
[F] = FKP /[ny] =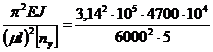 
= 254 ×103 Н = 254 кН
11
