Урок: «Умножение вектора на число»

ГЕОМЕТРИЯ.

УРОК: «УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО»

Предмет: Геометрия

Тема: Умножение вектора на число

Класс: 9 класс
Педагог: , заместитель директора по воспитательной работе, учитель математики и информатики.

Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область

Учащиеся должны:

Знать определение умножения вектора на число, свойства умножения вектора на число; знать правила действий с векторами

Уметь использовать свойства и определение при решении задач.

Ход урока.

I. Организационный момент: назвать цели урока.

II. Проверка пройденного материала:

Тестирование:

1. Вставьте пропущенное слово.

Вычитание векторов, как и вычитание чисел, - это действие, ... сложению

( обратное)

2. Что утверждает теорема о разности двух векторов?

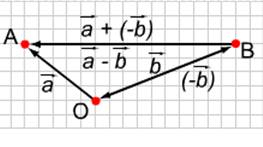
А) Для любых векторов и справедливо равенство: - = + (-).

Б) Для любых векторов и справедливо равенство: + =+

В)Для любых и справедливо равенство: ( + )+ = + (+)

III. Объяснение нового материала.

План объяснения.

1. Произведение вектора на число.

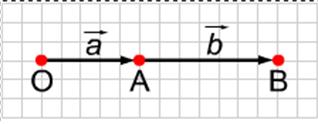
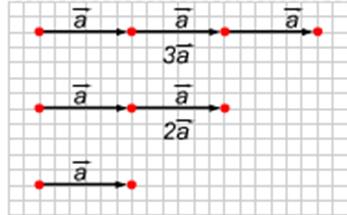
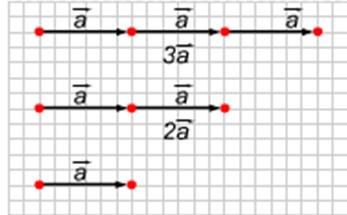Определив сложение двух векторов, мы можем рассмотреть суммы вида: а+а, а+а+а и т. д.. Такие суммы, как и в алгебре, обозначаются 2а,3а и т. д. (рисунок1). Этот пример показывает, что удобно ввести операцию умножения вектора на число, и подсказывает, как дать соответствующее определение.

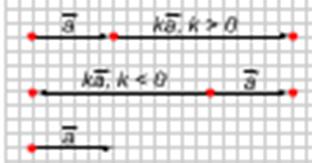Произведением ненулевого вектора на число k называется такой вектор, длина которого равна ½ k½*½½, причем векторы и сонаправлены при k ³ 0 и противоположно направлены при k <0.

Произведением нулевого вектора на любое число считается нулевой вектор.

2. Следствия из определения:

1. 1 = для любого вектора.

Действительно, если ¹0, то по определению ½1½ =½1½½½ =½½ и т. к. k=1 >0, то

1Þ 1 =. Если =0, то1 =0Þ 1 = для любого вектора.

2. (-1) = - для любого вектора .

Действительно, если ¹0, то ½(-1) ½ = ½-1½½½=½½ и т. к. k=-1 <0, то (-1) =0Þ

(-1) = - для любого вектора .

3. Если k =0, то либо k=0, либо =0.

Действительно, если k =0, то ½ k½=½ k½½½=0, т. е. либо ½ k½=0, либо ½½=0, что и означает, либо k=0, либо =0.

4. Если k = k и k¹0, то =.

Действительно, если ½ k½=½ k½, то ½ k½½½=½ k½½½, отсюда ½½=½½. Если k >0, то k, k, а т. к. k = k, .

Если же k<0, то k, k, а т. к. k = k, то.

Итак,½½=½½ и , т. е. =

3. Отработка навыков с помощью тренажера.

Введите с клавиатуры недостающие числа.

4. Законы умножения вектора на число

Умножение вектора на число подчиняется тем же законам, что и умножение чисел. Докажем три закона, справедливые для любых векторов и и любых чисел k и m.

1.( k + m) = k+ m ( I распределительный закон)

2. k( + ) = k+ k ( II распределительный закон)

3. (k m) = k (m) ( сочетательный закон)

I Распределительный закон.

Доказательство:

1. Докажем, что (k + m) = k+ m для любого вектора и любых чисел k и m.

При k = m=0 справедливость ( k + m) = k+ m очевидна для любого вектора

При k = 0 m¹0 получается равенство m = m , верное для любого вектора и любого числа m (аналогично в случае k¹0 и m= 0) . При k¹0 и m¹0 предположим, что ½ k½ ³½ m½, т. е. k¹0 и £ 1, тогда вектор + .

Кроме того, 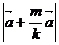= ½½+ ½½ = (1 +)½½.

Следовательно, согласно определению произведения вектора на число

+ = (1 +).

Умножив это равенство на k¹0, получим требуемое: ( k + m) = k+ m . Итак, мы доказали, что ( k + m) = k+ m для любого вектора и любых чисел k и m.

2. Докажем, что k( + ) = k+ k для любых векторов и и любого числа k.

При k=0 справедливость k( + ) = k+ k очевидна для любых векторов и .

При k¹0 ( случай рассматривается аналогично).

Отложим от произвольной точки О вектор = , затем от точки А вектор =. Тогда вектор = + .. т. к. , то ½ + ½ = ½ ½ + ½½. По определению произведения вектора на число что½ k( + )½ = ½k½½+ ½= ½k½½½+ ½k½½½. Если k, то, т. к. >0 , получим k( + ) и k+ k. Отсюда k( + ) k+ k, следовательно, k( + ) = k+ k. Если k<0, то k( + ), k, k. Тогда k( + ) k+ k. Следовательно, k( + ) = k+ k

Пусть теперь векторы и неколлинеарные. Отложим от произвольной точки О векторы = и = k, а от точки А1 и А - векторы = и = k. Случаю k >0 соответствует представленный рисунок. Т. к., согласно определению произведения вектора на число, векторы k и коллинеарные, то прямые АВ и А1В1 параллельны. Тогда D ОАВ ~ D ОА1В1 по двум углам (Ð ОАВ =ÐОА1В1 как соответственные при АВ½½А1В1 угол при вершине О - общий) , причем k - коэффициент подобия. Следовательно, = k

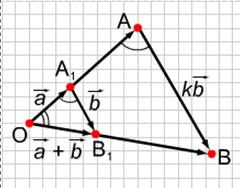По правилу треугольника = + . Тогда =k ( + ). С другой стороны, = + = k+ k. Итак, k( + ) = k+ k.

II Распределительный закон.

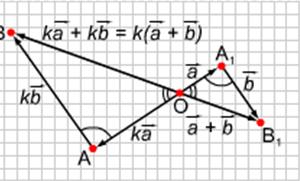На рисунке рассмотрен случай: когда k<0. Тогда аналогично D ОАВ ~ DОА1В1 по двум углам (Ð ОАВ =ÐОА1В1 как накрест лежащие при АВ ½½А1В1, Ð ВОА =Ð В1 ОА1 как вертикальные) причем½ k½ - коэффициент подобия. Следовательно, = k. По правилу треугольника = + . Тогда =k ( + ). С другой стороны, = += k+ k. Итак, мы доказали, что k( + ) = k+ k.

Сочетательный закон.

Докажем, что k(m) = (km) для любого вектора и любых чисел k и m. При k=0 или m=0 или =0 справедливость k(m) = (km) очевидна для любого вектора и любых чисел k и m.

При k¹0, m¹0 и ¹0, получим, что ½(km)½ = ½km½½½=½k½½m½½½=½ k½½ m½=½ k(m)½.

Если km>0, то (km) и k(m).

Если km <0, то(km) и k(m).

В каждом случае (km) k(m) и ½ (km) ½=½ k(m)½, следовательно, k(m) = (km) . Итак, мы доказали, что k(m) = (km) для любого вектора и любых чисел k и m.

В силу доказанных свойств умножения вектора на число можно составлять векторные выражения, аналогичные многочленам первой степени в алгебре. Эти выражения можно преобразовывать так же, как преобразуются соответствующие алгебраические выражения, т. е. приводить подобные члены, раскрывать скобки, выносить за скобки общий множитель, переносить члены из одной части равенства в другую с обратным знаком действия и т. д.

Например, 2(3а-4b +c) -3(2a +b -3c) =6a -8b +2c -6a -3b +9c = -11b +11c=11(c-b).

5. Векторный метод.

Операции с векторами составляют основу векторной алгебры - раздела математики, изучающего векторы и действия с векторами. Векторы могут использоваться для решения геометрических задач и доказательства теорем.

Далее, вы увидите, как применяется векторный метод на примере доказательства уже известных вам теорем о средней линии треугольника и трапеции.

Решение задач и доказательство теорем состоит из трех этапов подобно тому, как это происходит при решении текстовых задач. Сначала условие задачи надо записать в векторном виде, введя подходящим образом векторы (аналогично составляются алгебраические уравнения). Потом с помощью известных вам действий над векторами исходное условии задачи, записанное в векторной форме, нужно преобразовать, т. е. привести к такому виду, который дает решение задачи в векторном виде ( аналогично решению алгебраического уравнения). Наконец, на последнем этапе на основании полученных векторных соотношений ответ формулируется уже в исходных терминах ( аналогично дается ответ на текстовую задачу, исходя из решений алгебраического уравнения).

6. Средняя линия треугольника.

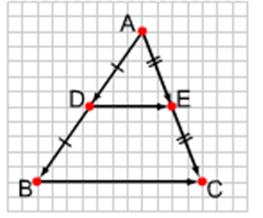Теорема. Средняя линия треугольника параллельна одной из его сторон и равна ее половине.

Пусть в D АВС: D ÎАВ, Е ÎАС, причем АD = DB, BE =EC.

Докажем, что DE ½½ВС и 2 DE = ВС.

Запишем условия задачи в векторной форме: = - = - = ( - ) =

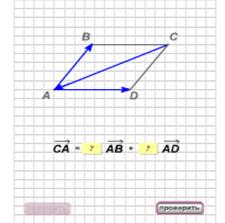
Отработка навыков с помощью тренажера.

Укажи векторы, которые являются коллинеарными.

Введите недостающее число в формуле

7. Свойство средней линии трапеции.

Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме.

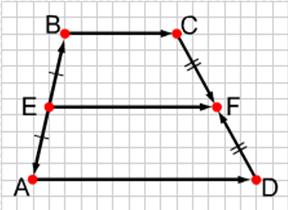
Доказательство:

Пусть в трапеции АВСD, EF - средняя линия.

Докажем, что EF½½ АD, EF½½ВС и EF=

Запишем условие задачи в векторной форме: , = - , = -

Т. к. по правилу многоугольника =++ и =++. Сложим эти равенства и сгруппируем слагаемые следующим образом:

2=(+)+(+)+(+). Т. к. при сложении противоположных векторов в сумме получается нулевой вектор, то 2 =0+++0 , отсюда EF=. Теорема доказана.

Выводы по теме:

1. Произведением вектора ¹0 на число k¹0 называется такой вектор k, для которого выполняются два условия:

1) модуль вектора k равен произведению модуля числа k и модуля вектора , т. е. ½ k½=½ k½½½

2) вектор k сонаправлен с вектором , если k >0, и направлен противоположно вектору , если k<0.

2. Для любого вектора и любых чисел k и m выполняется первый распределительный закон: (k+m) = k+ m

3. Для векторов и и любого числа k выполняется второй распределительный закон:

k( + ) = k+ k.

4. Для вектора и любых чисел k и m выполняется сочетательный закон k(m) = (km)

5. Теорема: Средняя линия треугольника параллельна одной из сторон и равна половине этой стороны.

6. Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме.

IV. Закрепление полученных знаний:

Тестирование:

1. Каким условиям удовлетворяет произведение k ненулевого вектора на число k?

А) вектор k сонаправлен с вектором , если k >0 и направлен противоположно вектору

Б) вектор k сонаправлен с вектором

В) вектор k направлен противоположно вектору

2. № 000. Боковые стороны трапеции равны 23см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции

а) 12 см б) 10см в) 14см

3. № 000. Дана равнобедренная трапеция АВСD. Перпендикуляр, опущенный из вершины В на большее основание AD делит это основание на два отрезка, больший из которых равен 7 см. Найдите среднюю линию трапеции.

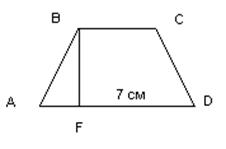а) 8см б) 6см в) 7см

V. Подведение итогов.

VI. Задание на дом: п.76-85, №№ 000,782,784