ПОСТРОЕНИЕ СЕТЕВОГО ГРАФИКА
Сетевой график или стреловидная диаграмма представляет собой ориентированный граф без контуров. Ориентированным граф называется потому, что стрелками показаны направления его ребер (дуг). Отсутствие контуров создает условия, при которых, двигаясь по направлению стрелок, через каждое ребро можно пройти только один раз. Сетевой график позволяет наглядно показать последовательность и взаимосвязь работ, входящих в программу или какой-либо план действий. Работы на такой диаграмме изображаются дугами. Таким образом, каждая дуга сетевого графика, имеющая вид стрелки, обозначает начало и конец работы, представляющее собой событие. Эти события будем изображать кружками. Кружок вначале стрелки будет начальным событием для работы, показанной данной стрелкой. Кружок в конце стрелки – конечным событием данной работы и начальным для последующей работы.
Граф, применяемый для построения сетевого графика, обладает еще одним свойством – у него нет висячих вершин. В этом случае все события на графике, кроме исходного и завершающего программу или план действия, имеют как предшествующие, так и последующие работы. Стрелки, входящие в кружок, обозначающий событие, будут отображать предшествующие работы. Стрелки, выходящие из кружка, характеризующего событие, будут показывать последующие работы. Исходное событие изображается кружком, из которого только выходят стрелки. Завершающее событие характеризуется тем, что у него имеются только входящие стрелки (предшествующие работы).
Построение сетевого графика требует соблюдения ряда правил.
Правило 1. Последовательность следующих друг за другом работ изображаются в виде цепи стрелок, соединенных друг с другом кружками. Например: работа б должна следовать за работой а (а ® б), работа в должна выполняться после завершения работы б (б ® в) и, наконец, работа в непосредственно предшествует работе г (в ® г). Такая последовательность работ на сетевом графике будет иметь следующий вид (рис. 3.3.2):

Правило 2. Несколько работ, одновременно непосредственно предшествующие какой-либо одной последующей работе, называются сходящимися. Например: работе г непосредственно предшествуют работы а, б и в (а, б, в ® г). Эта ситуация на сетевом графике должна изображаться так, как показано на рис. 3.3.3.
 |
Правило 3. Несколько работ, непосредственно следующие за одной какой-либо предшествующей работой, называются расходящимися. Например: работа а непосредственно предшествует работам б, в и г (а ® б, в, г). На сетевом графике данная ситуация должна будет иметь вид, показанный на рис. 3.3.4.
 |
Правило 4. На сетевом графике не должны показываться не существующие связи последующих и непосредственно предшествующих работ. Например: работы а, б, в предшествуют работе г (а, б, в ® г), вместе с тем, работа а непосредственно предшествует работе д (а ® д). На сетевом графике эта ситуация должна отображаться способом, показанным на рис. 3.3.5 (а) и не может изображаться способом, показанным на рис. 3.3.5 (б), так как в последнем случае будут иметь место несуществующие связи между работами б, в и д.
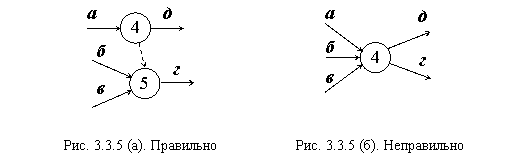
На рис. 3.3.5 (а) штриховая стрелка изображает фиктивную работу (4–5), указывающую на то, что работа г не может начинаться до завершения работы а. Такая работа не требует времени или каких-либо других ресурсов для ее выполнения. Она служит лишь для отражения существующей связи между работами а и г.
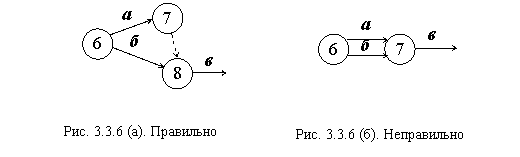
Правило 5. Любые два соседних события на сетевом графике могут быть соединены одной стрелкой. Это означает, что при параллельном выполнении работ для отображения указанной ситуации возникает необходимость введения дополнительного события и фиктивной работы. Например: работы а, б, выходящие из события 6, являются непосредственно предшествующими для работы в (а, б ® в). Эта ситуация должна изображаться способом, показанном на рис. 3.3.6 (а) и не может изображаться способом, показанном на рис. 3.3.6 (б).
При построении сетевого графика удобно пользоваться технологией, показанной на рис. 3.3.7. В данном случае рассматривается построение сетевого графика для выполнения проекта, включающего в себя 11 работ, обозначенных буквами. Работы проекта имеют следующие технологические связи:
® а, д, е, ж
а ® б, в
в ® г
ж ® з
е, з ® к, л
г, д, к, ® н
ж, л ® о
![]() б, н ® п
б, н ® п
о, п ®
![]()
![]() В перечне связей знаком обозначено исходное событие комплекса работ, а знаком – завершающее событие.
В перечне связей знаком обозначено исходное событие комплекса работ, а знаком – завершающее событие.
Построение сетевого графика не достаточно для контроля и управления ходом выполнения проекта. Необходим расчет ряда параметров сетевого графика и определение критического пути. Всякая последовательность работ на сетевом графике, имеющая начало в исходном событии, а конец – в завершающем, называется полным путем. Полный путь, требующий максимальных затрат времени, называется критическим путем. Любая другая последовательность работ представляет собой просто путь.
Для контроля и управления ходом работ по сетевому графику необходим расчет следующих параметров:
1. Необходимое для выполнения каждой отдельной работы время. Его называют ожидаемым временем (![]() ). Поскольку действительно необходимое время может зависеть от множества факторов, его определяют как вероятностную величину на основе экспертных оценок предполагаемых исполнителей. Определение ожидаемого времени на выполнение работы может осуществляться либо по двум, либо по трем экспертным оценкам. На основе двух оценок расчет
). Поскольку действительно необходимое время может зависеть от множества факторов, его определяют как вероятностную величину на основе экспертных оценок предполагаемых исполнителей. Определение ожидаемого времени на выполнение работы может осуществляться либо по двум, либо по трем экспертным оценкам. На основе двух оценок расчет ![]() осуществляется по следующей формуле:
осуществляется по следующей формуле:
![]() ,
,
где ![]() – пессимистическая оценка эксперта, предполагающая задержки не по вине исполнителя;
– пессимистическая оценка эксперта, предполагающая задержки не по вине исполнителя;
![]() – оптимистическая оценка эксперта, предполагающая отсутствие непредвиденных задержке.
– оптимистическая оценка эксперта, предполагающая отсутствие непредвиденных задержке.
 |
По трем экспертным оценкам расчет ![]() осуществляется по такой формуле:
осуществляется по такой формуле:
![]() ,
,
где кроме рассмотренных выше оценок ![]() и
и ![]() используется оценка наиболее вероятного времени
используется оценка наиболее вероятного времени ![]() , которое потребуется для выполнения данной работы.
, которое потребуется для выполнения данной работы.
2. Раннее время свершения каждого события (![]() ). Оно представляет собой минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию, и равный максимальному по длительности пути от исходного события до рассматриваемого. Расчет его можно проводить по следующей формуле:
). Оно представляет собой минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию, и равный максимальному по длительности пути от исходного события до рассматриваемого. Расчет его можно проводить по следующей формуле:
![]() ,
,
где i – номер начального события для данной работы;
j – номер конечного события.
Например:
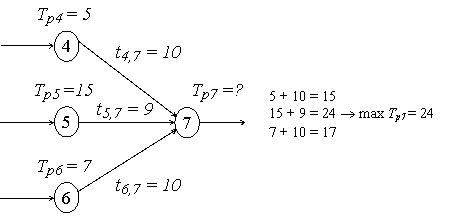 |
Расчет раннего времени свершения событий начинается с исходного, у которого ![]() .
.
3. Позднее время свершения каждого события ( ). Оно представляет собой максимальный из допустимых срок, необходимый для выполнения всех предшествующих работ без изменения продолжительности критического пути. Расчет его можно осуществить на основе следующей формулы:
![]() ,
,
где i и j имеют те же значения, что и в предыдущем случае.
Например:
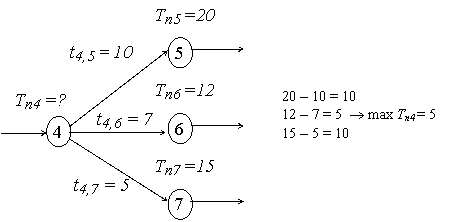 |
Расчет позднего времени свершения событий начинается с завершающего, у которого ![]() .
.
4. Резерв времени событий, то есть время, на которое может быть отсрочено наступление соответствующего события. Оно равно разности между поздним и ранним сроками свершения события.
![]() .
.
5. Полный резерв времени работы показывает время, на которое может быть увеличена продолжительность работы без изменения длительности критического пути. Если при выполнении какой-либо работы будет израсходован весь полный ее резерв времени, то все другие работы данного пути, следующие за ней, не будут иметь резервов времени. Расчет полного резерва времени работы (![]() ) осуществляется по следующей формуле:
) осуществляется по следующей формуле:
![]() .
.
6. Свободный резерв времени показывает время, на которое может быть увеличена продолжительность работы без изменения резервов времени последующих работ, лежащих на данном пути. Расчет свободного времени работы (![]() ) осуществляется по формуле:
) осуществляется по формуле:
![]() .
.
Свободный резерв времени, так же как и полный, позволяют менеджерам вносить коррективы в управляемый процесс на основе данных текущего контроля. Разница заключается в том, что свободным резервом времени можно позволить распоряжаться и исполнителям, поскольку это не повлияет на другие работы программы, а использование полного резерва требует учета возможностей исполнителей последующих работ.
7. Коэффициент напряженности работ (![]() ) характеризует степень свободы в сроках начала и окончания работ, не лежащих на критическом пути. Работы критического пути не имеют резервов времени, и их коэффициент напряженности равен 1. У работ, не лежащих на критическом пути, этот коэффициент > 1. Расчет этого показателя осуществляется только для работ, не лежащих на критическом пути, по следующей формуле:
) характеризует степень свободы в сроках начала и окончания работ, не лежащих на критическом пути. Работы критического пути не имеют резервов времени, и их коэффициент напряженности равен 1. У работ, не лежащих на критическом пути, этот коэффициент > 1. Расчет этого показателя осуществляется только для работ, не лежащих на критическом пути, по следующей формуле:
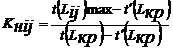 ,
,
где ![]() – длительность максимального пути, проходящего через данную работу;
– длительность максимального пути, проходящего через данную работу;
![]() –длительность отрезков критического пути, лежащих на рассматриваемом пути;
–длительность отрезков критического пути, лежащих на рассматриваемом пути;
![]() – длительность критического пути.
– длительность критического пути.
При условии взаимозаменяемости используемых в трудовом процессе ресурсов, перераспределение их следует проводить с учетом значения показателя ![]() .
.
То есть, перераспределение ресурсов надо начинать с работ, имеющих минимальный коэффициент напряженности, и направлять их на работы с максимальным коэффициентом напряженности* [6].
Ленточные графики Ганта – это отображение прохождения какого-либо процесса отрезками прямых линий на графике, осями координат которого служат время и операции (работы) рассматриваемого процесса. Способ его применения для контроля загрузки оборудования и для выработки решения о времени остановки отдельных единиц оборудования на профилактический ремонт показан на рис. 3.3.8. Например, фрезерный станок 3 загружен лишь 24.09 и 25.09. Следовательно, первые три дня недели его можно загрузить неплановой работой или провести его профилактический ремонт, как это предусмотрено по графику для сверлильного станка 1 на 21.09 и 22.09. Ленточный график Ганта можно использовать в качестве плана осуществления технологического процесса производства изделий. На рис. 3.3.8 можно увидеть пример фрагмента такого плана. Партия деталей А 21.09 и четверть рабочего дня 22.09 должна проходить обработку на токарном станке 1. Затем три четверти рабочего времени 22.09, полный рабочий день 23.09 и четверть 24.09 эти детали должны обрабатываться на фрезерном станке 1. После выполнения названных операций партия деталей А 24.09 передается на сверлильный станок 1.
График Ганта показывает требующееся на выполнение работы время и последовательность. На графике не видно взаимосвязей выполняемых работ, и поэтому трудно принимать решения об изменении их последовательности.
Ленточный график не показывает взаимосвязей работ, но он более наглядный при использовании его для контроля времени начала и окончания отдельных работ. Эта особенность делает предпочтительным совместное применение сетевого и ленточного графика Ганта.
Предположим, что требуется подготовить производство и изготовить прибор. Сделать это необходимо в кратчайшие сроки, которые должны быть согласованы с заказчиком. Контроль и управление этим проектом менеджер предполагает осуществить с помощью сетевого и ленточного графика Ганта.
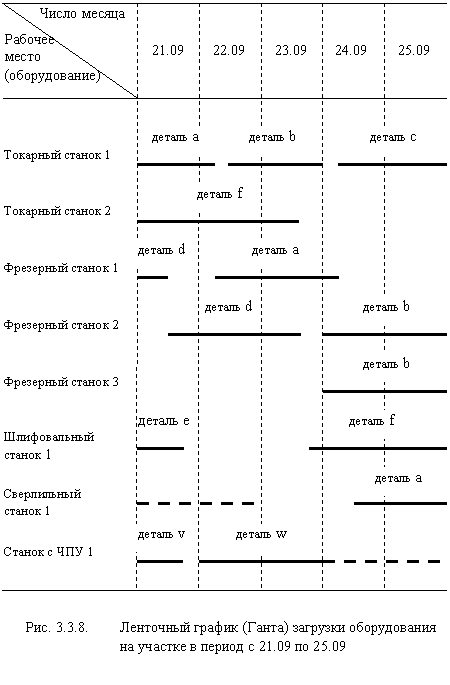
Сначала разрабатывается перечень необходимых работ и их взаимосвязи. Затем строится сетевой график (рис. 3.3.9) и, используя экспертные оценки предполагаемых исполнителей, рассчитываются ![]() для каждой работы (табл. 3.3.3).
для каждой работы (табл. 3.3.3).
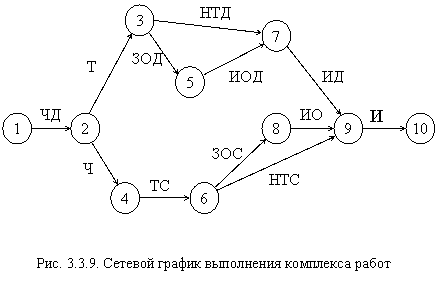
Таблица 3.3.3
Код работ | Наименование работ | Продолжительность работ в днях |
1–2 | Разработка рабочих чертежей деталей (ЧД) | 10 |
2–3 | Разработка технологических процессов изготовления деталей (ТД) | 10 |
2–4 | Разработка чертежей сборочных единиц (ЧС) | 3 |
3–5 | Проектирование и заказывание оснастки для производства деталей (ЗОД) | 10 |
3–7 | Нормирование операций технологического процесса по изготовлению деталей (НТД) | 2 |
4–6 | Разработка сборочных технологических процессов (ТС) | 3 |
5–7 | Изготовление оснастки для выполнения операций технологических процессов производства деталей (ИОД) | 12 |
6–8 | Проектирование и заказывание оснастки для осуществления сборки изделия (ЗОС) | 2 |
6–9 | Нормирование операций технологического процесса по сборке изделия (НТС) | 2 |
7–9 | Изготовление деталей изделия (ИД) | 8 |
8–9 | Изготовление оснастки для выполнения сборочных работ (ИОС) | 5 |
9–10 | Сборка и испытание изделия (ИС) | 2 |
На основе полученной информации выполняется расчет параметров сетевого графика. Расчет будем выполнять непосредственно на графике. Для этого введем следующую форму обозначения данных:
Перестроив сетевой график на рис. 3.3.9 с учетом отражения на нем указанной выше информации, осуществим расчет параметров по сформулированным выше правилам. В результате получим изображение данного сетевого графика в форме, показанной на рис. 3.3.10.
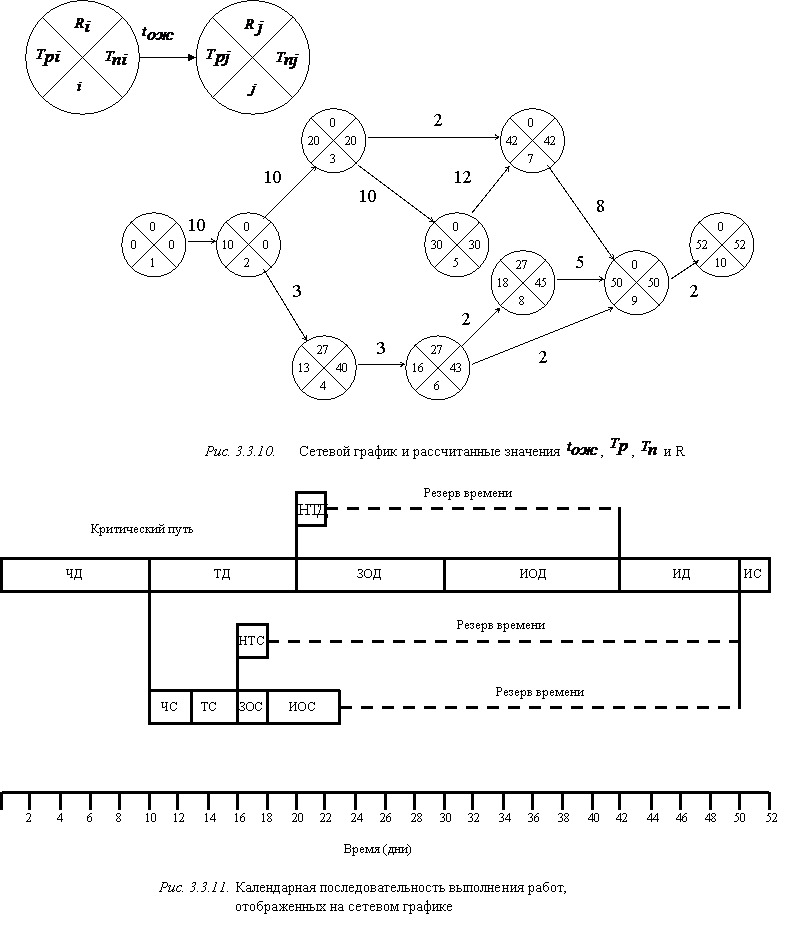
Для визуального анализа комплекса работ и напряженности их своевременного выполнения выполним «привязку» сетевого графика к шкале времени (рис. 3.3.11).
Как видно из схемы (рис. 3.3.11), работы сетевого графика образовали четыре полных пути. Первый путь: ЧД – ТД – НТД – ИД – ИС, на котором работа НТД имеет полный резерв времени – 20 дней. Второй путь: ЧД – ТД – ЗОД – ИОД – ИД – ИС, где ни одна работа не имеет резерва времени, и потому он называется критическим путем. Третий путь: ЧД – ЧС – ТС – НТС – ИС, на котором работа НТС имеет полный резерв времени, равный 32 дням. Четвертый путь: ЧД – ЧС – ТЧ – ЗОС – ИОС – ИС, где работы ЧС, ТЧ, ЗОС и ИОС имеют полный резерв времени, равный 27 дням. Этот резерв времени может быть использован при выполнении одной из названных работ или поделен между перечисленными работами.
Таблица 3.3.4
Сводная таблица параметров сетевого графика
Начальное событие | Конечное событие |
|
|
|
|
|
|
|
1 | 2 | 10 | 10 | 10 | 0 | 0 | 0 | 1 |
2 | 3 | 10 | 20 | 20 | 0 | 0 | 0 | 1 |
2 | 4 | 3 | 13 | 40 | 27 | 27 | 0 | 0,32 |
3 | 5 | 10 | 30 | 30 | 0 | 0 | 0 | 1 |
3 | 7 | 2 | 42 | 42 | 0 | 20 | 20 | 0,09 |
4 | 6 | 3 | 16 | 43 | 27 | 27 | 0 | 0,32 |
5 | 7 | 12 | 42 | 42 | 0 | 0 | 0 | 1 |
6 | 8 | 2 | 18 | 45 | 27 | 27 | 0 | 0,32 |
6 | 9 | 2 | 50 | 50 | 0 | 32 | 32 | 0,2 |
7 | 9 | 8 | 50 | 50 | 0 | 0 | 0 | 1 |
8 | 9 | 5 | 50 | 50 | 0 | 27 | 27 | 0,32 |
9 | 10 | 2 | 52 | 52 | 0 | 0 | 0 | 1 |
Для удобства практической работы по контролю и маневрированию ресурсов рассчитанные параметры сведем в таблицу 3.3.4, а последовательность выполнения работ изобразим в виде ленточного графика Ганта (рис. 3.3.12). Из таблицы видно, что работа 3–7 (НТД) имеет свободный резерв времени, равный 20 дням, работа 6–9 (НТС) – 32 дня, и работа 8–9 (ИОС) – 27 дней. Это показывает возможность представить свободу в планировании начала этой работы, но откладывать указанные работы можно лишь в пределах свободного резерва времени.
На ленточном графике Ганта показаны числа календаря для начала и окончания каждой работы. В верхней части графика изображен критический путь. За работами этого пути менеджер должен вести постоянный контроль и предпринимать управленческие действия, предупреждающие нарушение сроков выполнения данных работ 18 января, 1 февраля, 15 февраля, 3 марта, 16 марта и 18 марта. Относительно работ, которые должны быть завершены 21 января, 26 января, 28 января, 3 и 4 февраля, достаточно докладов исполнителей об их окончании. В ходе выполнения в возникающие непредвиденные ситуации можно не вникать, если не поступит просьба от исполнителя.
 |

* Более подробно вопросы построения, расчета параметров и теоретические обоснования применяемых формул в работе: Сетевые графики в планировании. Учеб. пособие / , , – 3-е изд. перераб. и доп. – М.: Высшая школа, 1981.



