Основы планирования межотраслевого баланса

ОСНОВЫ ПЛАНИРОВАНИЯ МЕЖОТРАСЛЕВОГО БАЛАНСА

Важнейшая задача дальнейшего совершенствования пла­нирования - улучшение сбалансированности производства, причем производства именно той продукции, которая нужна для развития производства и удовлетворения растущего спро­са населения. Для этого используется ряд экономико-матема­тических моделей, в том числе межотраслевые балансы.

Центральная идея межотраслевого баланса заключается в том, что каждая отрасль в нем рассматривается и как произ­водитель и как потребитель. Модель межотраслевого баланса - одна из самых простых экономико-математических моде­лей. Она представляет собой единую взаимоувязанную систему информации о взаимных поставках продукции между всеми отраслями производства, а также об объеме и отраслевой структуре основных производственных фондов, об обеспечен­ности народного хозяйства ресурсами труда и т. д.

Такая модель позволяет рассчитать сбалансированный план на основе точного учета всех межотраслевых связей и рассмотреть при этом множество возможных вариантов.

В основе исследований балансовых моделей лежат ба­лансовые таблицы, содержащие данные о производстве и потреблении продукции различных отраслей или предприя­тий. Такие балансы затрат выпуска продукции отражают слож­ные взаимосвязи между различными отраслями производства, характеризуют общественно необходимые затраты в процес­се производства (производственное потребление), распреде­ление общественного продукта, всесторонний оборот мате­риальных ценностей и т. д.

В результате балансовых исследований могут быть изу­чены межотраслевые и межрайонные связи, рассчитаны пол­ные затраты труда, капиталовложений, энергии и т. д. на производство единицы общественного продукта, исследован подробно оборот материальных ценностей в данном хозяй­стве.

Характерные черты и особенности этого метода описы­ваются с помощью матричных моделей баланса. Из математи­ческих методов здесь главным образом используется аппарат линейной алгебры.

Модель межотраслевого баланса

Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть испол­нение баланса за предшествующий период характеризуется данными, приведенными в табл.1.

Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств произ­водства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэто­му каждая из рассматриваемых отраслей выступает и как производитель продукции (l-й столбец таблицы), и как ее потребитель (l-я строка таблицы).

Приведенную таблицу конкретного примера можно за­писать и в общем виде (табл.2).

Обозначим через валовый выпуск продукции -й отрас­ли за планируемый период и через - конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т. д.). Таким образом, разность составляет часть продукции -й от­расли, предназначенную для внутрипроизводственного по­требления. Предполагаем, что баланс составляется в стоимостном разрезе. Обозначим черезчасть продукции -й от­расли, которая потребляется -й отраслью, для обеспечения валового выпуска ее продукции в размере .

В общем виде имеем принципиальную схему межотрас­левого баланса (табл.2) для двух отраслей.

ТАБЛИЦА 1.

Таблица 2

Очевидно, величины, расположенные в строках, связа­ны следующими балансовыми равенствами

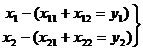(1)

Одна из задач балансовых исследований заключается в том, чтобы на базе данных об исполнении баланса за пред­шествующий период определить исходные данные на плани­руемый период.

Рассчитываем по данным таблицы коэффициенты пря­мых затрат. Это отношение количества продукции -й отрас­ли, поступающей в -ю отрасль для обеспечения выпуска ее продукции в размере , т. е.

, (2)

откуда (3)

т. е. затраты -ой отрасли в -ю отрасль пропорциональны ее валовому выпуску или, другими словами, зависят линейно от валового выпуска .

Выписанные соотношения называют условием линейности прямых затрат.

Рассчитываем

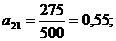
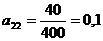
и записываем в табл.1 в углах соответствующих клеток. Найденные коэффициенты образуют матрицу прямых затрат

.

Все элементы этой матрицы неотрицательны. Это за­писывают в виде матричного неравенства и называют такую матрицу неотрицательной.

Заданием матрицы определяются все внутренние вза­имосвязи между производством и потреблением, характери­зуемые исходной табл.1.

Теперь можно записать линейную балансовую модель, соответствующую данным табл.1, если подставить значе­ния в балансовые равенства

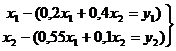(4)

или в матричной форме

, (5)

где

, ,,.

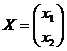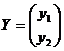Эта система двух уравнений может быть использована для определения и при заданных значениях и , для исследования влияния на валовый выпуск любых изменений в ассортименте конечного продукта, для определения мат­рицы коэффициентов полных затрат, элементы которой слу­жат важными показателями для планирования развития от­раслей и т. д.

Общая модель межотраслевого баланса продукции

Рассмотренная табл.2 есть не что иное, как одна из основных экономических моделей (данная в сокращенном виде), широко известных в нашей стране и за рубежом: меотраслевой баланс производства и распределения продук­ции в народном хозяйстве (МОБ).

В общем виде МОБ состоит из четырех основных час­тей - квадрантов (табл.3).

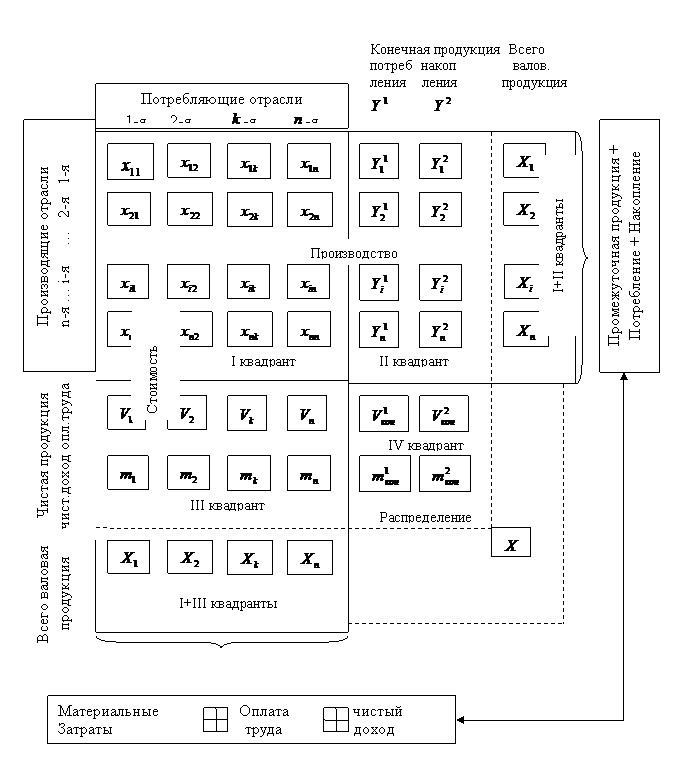
Таблица 3

I квадрант содержит показатели материальных затрат на производство продукции. По строкам и столбцам отрасли рас­полагаются в одинаковом порядке. Величина представляет собой стоимость средств производства, произведенных в -й отрасли и потребленных в качестве материальных затрат в -й потребляющей отрасли. Можно сказать, что сумма всех элементов квадратной матрицы -гo порядка, стоящей в пер­вом квадранте, равняется годовому фонду возмещения зат­рат средств производства в материальной сфере.

Во II квадранте показана конечная продукция, исполь­зуемая на непроизводственное потребление, накопление и экспорт. Тогда этот квадрант можно рассматривать как рас­пределение национального дохода на фонд накопления и фонд потребления по отраслям производства и потребления.

В III квадранте характеризуется национальный доход, но со стороны его стоимостного состава чистой продукции (оплата труда, прибыль, налог с оборота и др.).

В IV квадранте отражается перераспределение чистой продукции. В результате перераспределения первоначально созданного национального дохода образуются конечные до­ходы населения, предприятий, государства. Если все показа­тели МОБ записаны в денежном выражении, то по столбцам баланса они представляют формирование стоимости валовой продукции, а по строкам - распределение той же продук­ции в народном хозяйстве. Поэтому показатели строк и стол­бцов равны.

Валовая продукция отраслей представлена в табл.3 в виде столбца, расположенного справа от второго квадрата и в виде строки, расположенной под третьим квадрантом. Эти столбец и строка играют важную роль как для проверки пра­вильности самого баланса (заполнения квадрантов), так и для разработки экономико-математической модели межотрасле­вого баланса.

В целом межотраслевой баланс в рамках общей модели объединяет балансы отраслей материального производства, баланс совокупного общественного продукта, балансы наци­онального дохода, баланс доходов и расходов населения.

Исходя из формулы (2), разделим показатели любого столбца МОБ на итог этого столбца (или соответствующей строке), то есть на валовую продукцию. Получим затраты на единицу этой продукции , которые образуют матрицу прямых затрат :

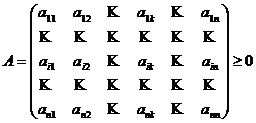. (6)

Стоимостной баланс наряду с уравнениями

, (7)

каждое из которых представляет распределение продукции данной отрасли по всем отраслям, допускает построение урав­нений в форме потребления продукции

, (8)

где - материальные затраты -й потребляющей отрасли, - ее чистая продукция ( - сумма оплаты труда, - чистый доход).

Подставляя в уравнения (7) соотношения (3), после преобразований получим

(9)

Систему уравнений МОБ (9) запишем в матричной форме

, (10)

где - единичная матрица, - матрица прямых затрат (6), и - столбцовые матрицы.

, .

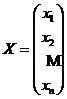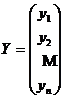Система уравнений (9), или в матричной форме (10) называется экономико-математической моделью межотраслевого баланса (моделью Леонтьева).

Модель межотраслевого баланса (10) позволяет решить следующие задачи:

1) определить объем конечной продукции отраслей 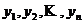по заданным объемам валовой продукции ;

2) по заданной матрице коэффициентов прямых затрат определить матрицу коэффициентов полных затрат , элементы которой служат важными показателями для планирования развития отраслей;

3) определить объемы валовой продукции отраслей 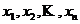по заданным объемам конечной продукции ;

4) по заданным объемам конечной или валовой продук­ции отраслей определить оставшиеся объемов.

Понятие о косвенных затратах

Прямые затраты играют в составлении баланса исклю­чительно важную роль. Они служат важной экономической характеристикой, без знания которой планирование народ­ного хозяйства не представлялось бы возможным.

Матрица прямых затрат по существу определяет струк­туру экономики. Если нам известны прямые затраты и конечный продукт каждой отрасли хозяйства, то мы можем вы­числить объем валовой продукции.

Чтобы выпустить автомобиль в Тольятти, нужно обеспе­чить электроэнергией не только сам завод, но и прокатные станы Магнитогорского комбината, и шинный завод в Ярос­лавле, и много других. Поэтому если прямо на один автомо­биль затрачивается 1,4 тысячи кВт' ч электроэнергии, то на всех промежуточных стадиях - еще 2 тысячи кВт' ч (кос­венные затраты электроэнергии), а всего 3,4 тысячи кВт' ч. Чтобы произвести 1 тонну штапельного волокна из лавса­на, требуется около пятидесяти тысяч рублей капитальных вложений непосредственно для завода химических воло­кон, а в сопряженных отраслях - еще около восьмидесяти тысяч рублей. Чтобы произвести на 1 О 000 рублей мясных изделий, капиталовложения в мясную промышленность дол­жны составить 900 рублей, а в других сопряженных отрас­лях -рублей, т. е. в 20 раз больше.

Таким образом, прямые затраты не отражают в полной мере сложных количественных взаимосвязей, наблюдающихся в народном хозяйстве. Они, в частности, не отражают обрат­ных связей, имеющих далеко не маловажное значение.

Как возникают косвенные затраты? На изготовление трактора в виде прямых затрат расходуется чугун, сталь и т. д. Но для производства стали также нужен чугун. Таким образом, кроме прямых затрат чугуна, имеются и косвенные затраты чугуна, связанные с производством трактора. В эти косвенные затраты входит и чугун, необходимый для созда­ния того количества чугуна, которое составляет прямые зат­раты. Эти косвенные затраты могут иногда существенно пре­вышать прямые затраты.

Полные внутрипроизводственные затраты

Система уравнений межотраслевого баланса в матричной форме была представлена в виде (10).

Пусть матрица , (11)

Где , тогда уравнение (10) запишется

, так как и , то или .

То есть объемы производства отраслей определяются как (12)

по заданным величинам конечного продукта потребления и матрице .

Матрицу называют матрицей коэффициентов полных затрат.

Элементы матрицы включают не только затраты -й продукции, необходимой для создания одной единицы -й продукции, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.

Значит, полные затраты включают как прямые , так и косвенные () затраты. Очевидно, что всегда .

Матрица коэффициентов полных затрат является суммой сходящегося матричного ряда

(13)

Матрицы называются матрицами коэффициентов косвенных затрат 2-ого, 3-его и т. д. порядков и коэффициенты полных затрат получаются в виде суммы коэффициентов прямых затрат и косвенных затрат.

Валовый выпуск k-й отрасли определяется как

(14)

Оптимизация межотраслевого баланса

Поскольку главной задачей экономики является улучше­ние производства, экономия человеческого труда, то возникла задача оптимизации модели народного хозяйства, по­строенной на основе МОБ.

Возможность оптимизации МОБ появляется, если коэффициенты прямых затрат отражают затраты не средние по отрасли, а для каждого способа и технологии производства. В таких моделях МОБ представлено отдельно производство мартеновской, конверторной стали, а также электростали; синтетических и хлопчатобумажных тканей и т. д. В результате должен быть найден оптимальный вариант с минималь­ными затратами на производство данного объема продукции.

Что значит составить оптимальный МОБ? Если для вычисления полных затрат и уровней цен надо решить сотни уравнений и выполнить миллионы вычислительных операций, то расчет оптимального МОБ - это миллионы уравнений и многие миллиарды вычислительных операций. В настоящее время еще нет математических методов и электронных ма­шин, чтобы решать такие задачи "в лоб". Еще нет в полном объеме и необходимых для этого данных. Теперь можно лишь говорить об отдельных важных блоках, для которых такие данные имеются или могут быть подготовлены в недалеком будущем.

Вот почему необходимо создание системы моделей для блочной оптимизации МОБ. Это должна быть гибкая система, которую могли бы по мере их готовности включаться все новые и новые оптимальные блоки.

Так как все производства прямо или косвенно связан друг с другом, то оптимизация каждого блока всякий раз, вызывает необходимость полного пересчета МОБ на ЭВМ. Работа большая, но результат несравненно больший - ведь за каждым процентом повышения эффективности общественного производства таятся миллиарды сэкономленных рублей.

Оптимизацию межотраслевого баланса покажем на примере сведения балансовых задач к задачам линейного программирования.

Пусть - ассортиментный вектор производства отраслей, а - вектор - конечный продукт, характеризующий то, что должно остаться к концу производственного цикла после внутрипроизводственного потребления, и - матрица затрат, где количество единиц продукта -й отрасли, идущее в качеств; внутрипроизводственного потребления в -ю отрасль на производство единицы -ого продукта.

Тогда величины , и связаны матричным уравнением (10)

.

Если матрица невырожденная, то решение (10) имеет вид .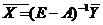

Допустим, что конечный продукт задан не точно, а ограничен снизу, т. е. .

Тогда система уравнений (10) заменится неравенствами 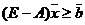(17)

Очевидно . Если при этом задан вектор оценки данного плана, где - оценка единицы продукта -й отрасли, то можно сформировать следующую задачу линейного программирования:

выбрать ассортиментный вектор , удовлетворяющий системе неравенств

(18)

Для которого линейная функция (19)

достигает минимума.

Вывод.

Отчетные межотраслевые балансы являются средством анализа структуры экономики и исходной базой составления межотраслевых балансов. Отчетные межотраслевые балансы разрабатываются на основе данных о структуре затрат на производство, получаемых от предприятий в результате специального единовременного обследования.

Разработка плановых межотраслевых балансов направлена в первую очередь на совершенствование балансового метода планирования, точное количественное выражение сложных взаимосвязей процесса общественного воспроизводства, расчет сбалансированных вариантов структуры народного хозяйства на основе широкого использования электронной вычислительной техники.