Вопросы к курсу «Исследование операций»
1. Предмет и цели исследования операций. Общие понятия
2. Общая характеристика и последовательность решения задач в исследованиях операций. Основные отличия метода исследования операций
3. Основные задачи, решаемые методом исследования операций. Классификация задач.
4. Методы отыскания оптимальных решений в задачах исследования операций. Классификация методов.
5. Экономико-математическое моделирование в теории исследования операций.
6. Постановка и модель задачи определения оптимального ассортимента продукции.
7. Постановка и модель задачи определения оптимального рациона питания (на примере).
8. Постановка и модель задачи определения оптимального использования мощностей оборудования.
9. Понятие задачи линейного программирования. Примеры.
10. Приведение задачи линейного программирования к канонической форме. Примеры.
11. Графическое решение задачи линейного программирования.
12. Симплекс-метод. Геометрическая интерпретация симплексного метода.
13. Взаимно двойственные задачи линейного программирования и их свойства.
14. Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов
15. Теоремы двойственности
16. Целочисленные задачи линейного программирования. Методы решения. Задача коммивояжера.
17. Постановка и экономико-математическая модель транспортной задачи.
18. Экономические задачи, сводящиеся к транспортным.
19. Методы составления первоначальных опорных планов в транспортной задаче. Пример
20. Системы управления запасами. Общие понятия. Модель оптимального размера заказа.
21. Назначение и области применения сетевого планирования и управления (СПУ). Сетевая модель и ее основные элементы. Порядок и правила построения сетевых графиков. Понятие о критическом пути.
22. Линейная диаграмма проекта. Временные параметры сетевых графиков.
Задачи для экзамена по курсу «Исследование операций» ИДО УлГТУ
1. Построить экономико-математическую модель следующей задачи распределения ресурсов: Предприятие изготавливает два вида продукции - П1 и П2, используюя два вида сырья - А и В. Суточные запасы сырья и его расход на единицу продукции вида П1 и вида П2 дан в табл.
Сырье | Расход сырья на 1 ед. продукции | Запас сырья, ед. | |
П1 | П1 | ||
А | 2 | 3 | 9 |
В | 1 | 2 | 10 |
Известно, что суточный спрос на продукцию П2 никогда не превышает 3 ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. - для П1 и 4 д. е. для П2.
Необходимо определить такие объемы суточного производства продукции П1 и продукции П2, при которых совокупный доход будет максимальным.
Решение:
а) Идентификация переменных задачи: модель строится для нахождения объемов суточного производства продукции П1 и продукции П2. Обозначим эти величины x1 и x2. Ясно, что x1 ≥ 0и x2 ≥ 0.
б) Смоделируем ограничения должны быть наложены на переменные:
Опишем строку матрицы, соответствующую сырью А.
Для производства продукции П1 в количестве x1 и продукции П2 в количестве x2 и потребуется сырье А в количестве 2x1 + 3x2, а запас сырья равен 9 единицам, следовательно должно выполняться неравенство
2x1 + 3x2 ≤ 9, (1)
соответствующее ограниченности сырья А.
Аналогично построим условие, соответствующее ограниченности сырья Б.
1·x1 + 2x2 ≤
в) смоделируем цель задачи:
Производств продукции П1 и П2 в в количестве x1 и x2 принесет доход в сумме 2x1 + 3x2. Цель производителя – получить максимальный доход. Следовательно, целевая функция задачи имеет вид
f(x) = 2x1 + 3x2 = max. (3)
Ответ:
Переменные задачи:
Целевая функция задачи: x1, x2 (причем естественно
f(x) = 2x1 + 3x2 = max.
Ограничения задачи:
2x1 + 3x2 ≤ 9,
1·x1 + 2x2 ≤ 10,
x1 ≥ 0,
x2 ≥ 0.
2. Привести задачу линейного программирования к канонической форме.
min f(x) = 6x1 + 4x2 ;
3x1 - x2 ≤ 2;
x1 + 2x2 ≥ 1;
x1 ≥ 0; x2 ≥ 0.
Решение:
а) Преобразование целевой функции:
Т. к. исходная целевая функция на оптимальном решении должна принимать минимальное значение, то она уже соответствует канонической форме и ее преобразовывать не надо.
б) Преобразование ограничений:
Правые части неравенств уже положительны. Чтобы неравенства превратить в равенства к левой части первого неравенства добавим новую неотрицательную переменную x3, а от левой части второго неравенства отнимем новую неотрицательную переменную x4. В результате получим два ограничения в виде равенств
3x1 - x2 + x3 = 2;
x1 + 2x2 - x4 = 1.
в) переменные x1, x2 неотрицательны по условию.
Ответ: Каноническая форма
min f(x) = 6x1 + 4x2 ;
3x1 - x2 + x3 = 2;
x1 + 2x2 - x4 = 1.
x1 ≥ 0; x2 ≥ 0.
3. Показать на координатной плоскости:
3.1. Полуплоскость, удовлетворяющую уравнению
x1 - 3x2 ≤
Решение:
а) Построим прямую
L: x1 - 3x2 =
Для этого найдем две точки А и В, принадлежащие прямой L.
т. А: положим x1 = 0, тогда из соотношения (5) получим
-3x2 = 2, т. е. x2 = -2/3 = -0,667.
Таким образом т. А имеет координаты (0, -0,667).
т. В: : положим x2 = 0, тогда из соотношения (5) получим
x1 = 2.
Таким образом т. В имеет координаты (2, 0).
б) Проверим – принадлежит ли начало координат (0, 0) искомой области. Подставим координаты x1 = 0, x2 = 0 в неравенство (4) и получим
0 ≤ 2,
т. е. неравенство выполняется и начало координат принадлежит искомой области (рис).
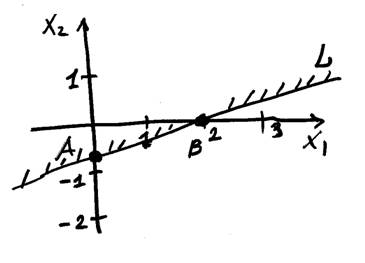
![]() Ответ: Искомая область лежит выше прямой L.
Ответ: Искомая область лежит выше прямой L.
3.2. Допустимую область удовлетворяющую системе ограничений:
x1 + 2x2 ≤ 4.
x1 ≥ 0; x2 ≥ 0.
Решение:
а) Построим прямую
L: x1 + 2x2 =
Для этого найдем две точки А и В, принадлежащие прямой L.
т. А: положим x1 = 0, тогда из соотношения (6) получим
2x2 = 4, т. е. x2 = 2.
Таким образом т. А имеет координаты (0, 2).
т. В: : положим x2 = 0, тогда из соотношения (6) получим
x1 = 4.
Таким образом т. В имеет координаты (4, 0).
б) Проверим – принадлежит ли начало координат (0, 0) искомой области. Подставим координаты x1 = 0, x2 = 0 в неравенство x1 + 2x2 ≤ 4 и получим
0 ≤ 4,
т. е. неравенство выполняется и начало координат принадлежит искомой области, задаваемой первым неравенством (рис).
б) Условие x1 ≥ 0 говорит о том, что искомая область лежит правее вертикальной оси координат (прямая L2).
Условие x2 ≥ 0 говорит о том, что искомая область лежит выше горизонтальной оси координат (прямая L3).
Результатом пересечения трех областей, определяемых прямыми L1, L2, L3 является треугольник ОАВ.
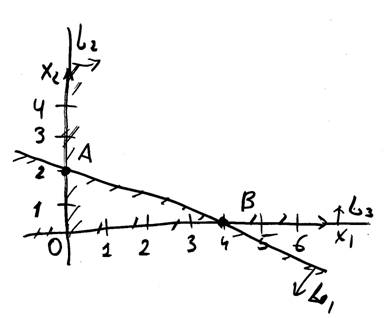
![]() Ответ: Искомая область есть треугольник ОАВ.
Ответ: Искомая область есть треугольник ОАВ.
5. Решить графическим способом задачу линейного программирования:
Целевая функция F = 3 х1 + 4х2 = max.
Ограничения:
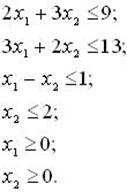
Решение
Построим многоугольник решений (рис.2.5). Для этого в системе координат X10X2 на плоскости изобразим граничные прямые:
2х1 + 3х2 = 9 (L1);
3х1 + 2х2 = 13 (L2);
х1 - х2 = 1 (L3);
х2 = 2 (L4).
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис. Показаны стрелками. Областью решений является многоугольник OABCD.
Для построения прямой Z = 3х1 + 4х2 = 0 строим вектор-градиент 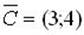 и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора
и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора ![]() . Из рис. следует, что по отношению к многоугольнику решений опорной эта прямая остановится в точке C, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L1 и L3. Для определения ее координат решим систему уравнений:
. Из рис. следует, что по отношению к многоугольнику решений опорной эта прямая остановится в точке C, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L1 и L3. Для определения ее координат решим систему уравнений:
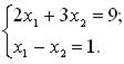
Оптимальный план задачи х1=2,4; х2=1,4. Подставляя значения х1 и х2 в линейную функцию, получим:
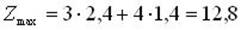 .
.
Полученное решение означает, что объем производства продукции П1 должен быть равен 2,4 ед., а продукции П2 – 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д. е.
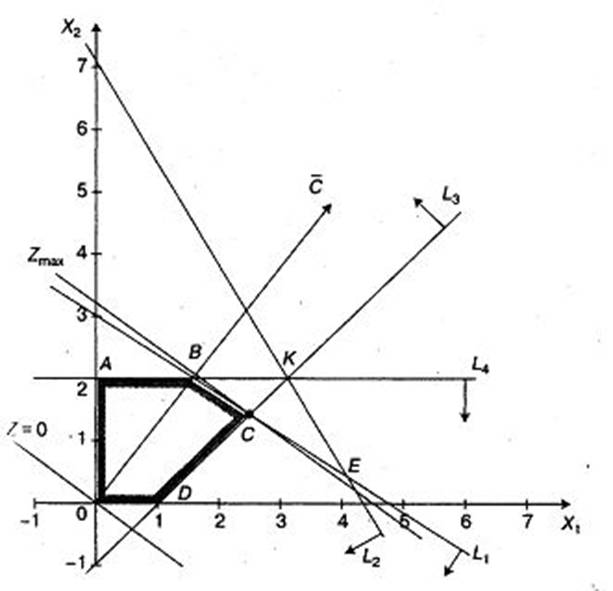
Рис. 2.5. Решение задачи линейного программирования геометрическим способом
6. Построить задачу, двойственную к следующей задаче линейного программирования:
![]() :
:
при ограничениях:
Решение.
1. Так как исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду ![]() , для чего обе части первого и четвертого неравенства умножим на -1. Получим
, для чего обе части первого и четвертого неравенства умножим на -1. Получим
2. Составим расширенную матрицу системы
3. Найдем матрицу ![]() , транспонированную к А
, транспонированную к А
4. Сформулируем двойственную задачу:
при ограничениях
7. Построить экономико-математическую модель следующей транспортной задачи (записать транспортную задачу в виде задачи линейного программирования).
Имеются три поставщика и четыре потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары "поставщик — потребитель" сведены в таблицу поставок (табл. 7.1).

В левом верхнем углу произвольной ![]() -клетки (i — номер
-клетки (i — номер
строки, j — номер столбца) стоит так называемый коэффициент затрат — затраты на перевозку единицы груза от i-го поставщика

Суммарные затраты F нa перевозку выражаются через коэффициенты затрат и поставки следующим образом:
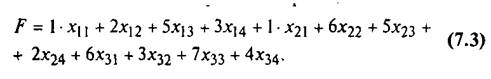
Теперь можно дать математическую формулировку задачи (без обращения к ее содержательному экономическому смыслу).
На множестве неотрицательных решений системы ограничений (7.1) и (7.2) найти такое решение![]() , при котором линейная функция (7.3) принимает минимальное значение.
, при котором линейная функция (7.3) принимает минимальное значение.
8. Для транспортной задачи построить опорный план методом "северо-западного угла" используя исходные данные задачи 7.
Найти первоначальное базисное распределение поставок для транспортной задачи 7.1.
Решение. Дадим переменной![]() максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) — "северо-западный" угол таблицы поставок:
максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) — "северо-западный" угол таблицы поставок:![]() = = min {60, 20} = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадет из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией (см. табл. 7.2) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. В таблице поставок найдем новый "северозападный" угол — клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60—20 единиц груза, получаем, что
= = min {60, 20} = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадет из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией (см. табл. 7.2) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. В таблице поставок найдем новый "северозападный" угол — клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60—20 единиц груза, получаем, что![]() = min {40, 110} = 40. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). В оставшейся таблице снова находим "северозападный угол" и т. д. В результате получаем следующее исходное распределение поставок (см. табл.7.2)>
= min {40, 110} = 40. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). В оставшейся таблице снова находим "северозападный угол" и т. д. В результате получаем следующее исходное распределение поставок (см. табл.7.2)>
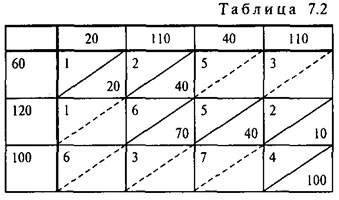
9. Для транспортной задачи построить опорный план методом " методом наименьших затрат " используя исходные данные задачи 7.
Решение. Находим в таблице поставок (си. табл. 7.1) клетки с наименьшим коэффициентом затрат. Таких клеток две — (1,1) и (2,1) с коэффициентами затрат, равными 1. Сравним максимально возможные поставки для этих клеток: для клетки (1,1) ![]() —
—![]() {60, 20} = 20, для клетки (2,1)
{60, 20} = 20, для клетки (2,1) 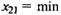 {120, 20} = = 20.
{120, 20} = = 20.
Так как они совпадают, то максимально возможную поставку даем в любую из них. Например, даем поставку, равную 20 единицам, в клетку (2,1). В результате спрос первого потребителя удовлетворен и первый столбец таблицы поставок выпадает из последующего рас смотрения (табл. 7.3).
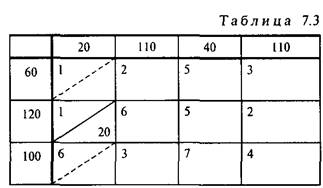
В оставшейся таблице наименьшим коэффициентом затрат обладают две клетки:![]() Сравним максимально возможные поставки для этих клеток: для клетки (1,2)
Сравним максимально возможные поставки для этих клеток: для клетки (1,2)![]() {60, 110} = 60; для клетки (2,4)
{60, 110} = 60; для клетки (2,4)![]() {120-20, 110} = 100. Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалась больше:
{120-20, 110} = 100. Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалась больше: ![]() = 100. При этом из рассмотрения выпадает вторая строка таблицы поставок (табл. 7.4).
= 100. При этом из рассмотрения выпадает вторая строка таблицы поставок (табл. 7.4).
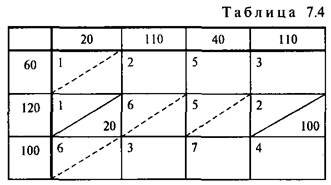
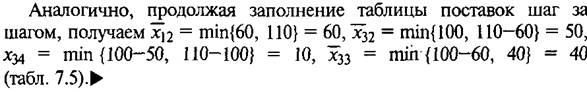
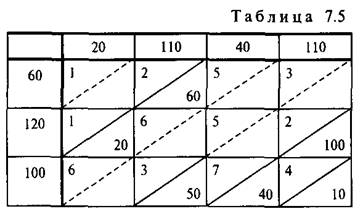
Сравним найденное распределение поставок с распределением, полученным для той же задачи по методу "северо-западного" угла (см. задачу 4.2, табл. 7.2). Вычислим для каждого из этих распределений суммарные затраты в денежных единицах: в задаче 7.2:
![]() = + 2 • 40 + 6 • 70 + 5 • 40 + 2 • 10 + 4 -100 = 1140; в задаче 7.3:
= + 2 • 40 + 6 • 70 + 5 • 40 + 2 • 10 + 4 -100 = 1140; в задаче 7.3:
![]() = 1 • 20 + + 3 • 50 + 2 • 100 + 7 • 40 + 4 • 10 = 810.
= 1 • 20 + + 3 • 50 + 2 • 100 + 7 • 40 + 4 • 10 = 810.
Как и ожидалось, при использовании метода "северо-западного" угла суммарные затраты больше, чем при применении метода наименьших затрат. Таким образом, во втором случае мы находимся ближе (по числу необходимых шагов) к оптимуму, чем в первом. Докажем, что распределения, получаемые с помощью указанных методов, являются базисными, и рассмотрим те особые случаи, которые могут встретиться при использовании этих методов.
10. Определить оптимальный размер Q* заказа и время между заказами t*.
Дано:
величина спроса за год D = 4000;
издержки заказа K = 25;
издержки хранения h = 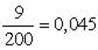 ;
;
цена за единицу с = 90;
время выполнения заказа L = 8;
ежедневный спрос d = 20;
число рабочих дней T = 200.
Решение
оптимальный размер заказа  ;
;
точка восстановления R = 160 – 149 = 11;
число заказов за год 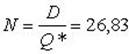 ;
;
совокупные издержки = совокупные издержки заказа + совокупные издержки хранения С = 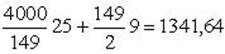 ;
;
стоимость продаж = 360000;
число дней между заказами t = 7,45.
11. По данным таблицы построить сетевой график, линейную диаграмму, определить полные пути, определить критический путь и его длину.
№ | Работы | Продолжи-тельность (сутки) | № | Работы | Продолжи-тельность (сутки) | |
1 | (1,2) | 5 | 5 | (2,6) | 9 | |
2 | (1,3) | 2 | 6 | (4,5) | 4 | |
3 | (1,4) | 7 | 7 | (5,6) | 3 | |
4 | (3,4) | 5 |
Решение
а) Сетевой график (Рис 11.1).
б) Полные пути: (1, 2, 6) длина пути t1 = 5+9=14;
(1, 3, 4, 5, 6) длина пути t1 = 2+5+4+3=14;
(1, 4, 5, 6) длина пути t1 = 7+4+3=14.
в) Все полные пути имеют одинаковую длину t =14, поэтому каждый из путей является критическим.
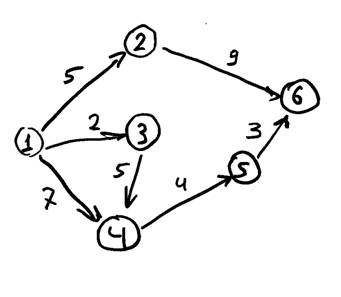
Рис 11.1 Сетевой график
г) Линейная диаграмма (Рис 11.2).
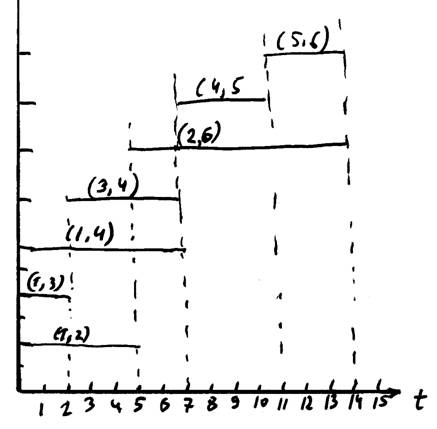
Рис 11.2 Линейная диаграмма



