ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Забайкальский институт железнодорожного транспорта
Кафедра «Прикладная механика и
инженерная графика»
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания
по выполнению контрольной работы
Чита
2013
УДК 531
ББК В21
Г 52
Рецензент
кандидат технических наук, доцент кафедры «Прикладная механика и инженерная графика»
Глазнев, В. А.
Г 52 Теоретическая механика. Методические указания по выполнению контрольной работы для студентов 2 курса заочной формы обучения специальности 190401.65 «Эксплуатация железных дорог»
. – Чита: ЗабИЖТ, 2013. –
Методические указания соответствуют государственному образовательному стандарту дисциплины «Теоретическая механика». В методических указаниях изложена методика решения контрольной работы на конкретных примерах. Предложены варианты контрольной работы для студентов 2 курса заочного факультета по разделу «Статика», «Кинематика», «Динамика».
© Забайкальский институт железнодорожного транспорта
(ЗабИЖТ), 2013
© Виктор Алексеевич Глазнев
ВВЕДЕНИЕ
Механика – наука о механическом движении и механическом взаимодействии материальных тел.
Кинематика – раздел механики, в котором изучаются движения материальных тел без учёта их масс и действующих на них сил.
Динамика – раздел механики, в котором изучаются движения механических систем под действием сил.
Статика – раздел механики, в котором изучаются условия равновесия механических систем под действием сил.
Целями освоения учебной дисциплины «Теоретическая механика являются:
1. Формирование навыков составления математических моделей механических систем.
2. Использование методов теоретической механики для исследования динамического и статического состояния различных технических объектов и систем.
Задачами освоения учебной дисциплины «Теоретическая механика являются:
1. Передача студентам теоретических основ и фундаментальных знаний в области теоретической механики.
2. Обучение умению применять знания, полученные в процессе изучения дисциплины, для решения прикладных задач при исследовании статического и динамического состояния технических объектов с использованием современного прикладного математического обеспечения.
В разработке представлены задания для контрольной работы по разделу
1. статика
− центр тяжести тел и фигур;
− определение реакции опор твёрдого тела.
2. кинематика
− Определение скорости и ускорения точки по заданным уравнениям её движения
3. Динамика
− Элементарная теория удара
Исходные данные для решения задач контрольных работ студенты должны брать из таблиц, приведенных в настоящих методических указаниях в соответствии со своим личным шифром по последней цифре. Например, при шифре 95-ЭЖД-123 следует выбирать 3 вариант.
1. ТРЕБОВАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
К оформлению контрольной работе предъявляются следующие требования:
- контрольная работа выполняется в тетради пастой одного цвета, кроме зеленого и красного;
- титульный лист (1 страница) оформляется в соответствии с требованиями оформления титульных листов контрольных работ;
- на страницах оставляются поля не менее 4 см;
- нумерация страниц обязательна;
- расчеты проводятся с точностью до двух значащих цифр после запятой;
- перед решением задачи выписывается ее условие с числовыми, а не буквенными значениями и приводится чертеж с числовыми размерами, выполненный схематично.
После получения проверенной работы студент должен исправить все ошибки с учетом сделанных замечаний. Перед зачетом или экзаменом по каждой контрольной работе проводится собеседование.
2. ПРОГРАММА курса
Программа определяет необходимый объем задач по дисциплине «Теоретическая механика». Степень охвата вопросов при изложении курсов, включенных в программу, определяется числом часов, отводимых по государственным образовательным стандартам.
Программа по теоретической механике рассчитана на объем курса в 216 часов (лекции, практические, самостоятельные занятия) для студентов заочной форм обучения «Эксплуатация железных дорог» в железнодорожном вузе.
2.1. Раздел 1. Статика
Тема 2.1.1. Основные понятия и аксиомы статики
Материальная точка. Абсолютно твердое тело. Сила; сила-вектор. Система сил. Перенос силы вдоль линии ее действия. Свободное и несвободное тело. Связи. Реакции связей.
Тема 2.1.2. Плоская система сходящихся сил
Система сходящихся сил. Разложение силы на две составляющие, приложенные в этой точке. Сложение плоской системы сходящихся сил. Проекция силы на ось (правило знаков); на две взаимно перпендикулярные оси. Уравнения равновесия системы сходящихся сил.
Тема 2.1.3. Пара сил
Пара сил. Вращающие действия пары сил на тело. Плечо пары, момент пары сил (правило знаков). Сложение пар. Условия равновесия плоской системы пар.
Тема 2.1.4. Плоская система произвольно расположенных сил
Момент силы относительно точки, условия равенства нулю. Приведение силы, системы сил к данному центру. Главный вектор, главный момент плоской системы сил.
Уравнения равновесия плоской системы сил, условия равновесия.
Основные виды эпюр балочных систем. Классификация нагрузок. Опорные реакции балочных систем.
Связи с трением. Трение скольжения, качения.
Тема 2.1.5. Центр тяжести
Центр параллельных сил. Формулы для определения положения центра тяжести тела. Определения положения центра тяжести простых фигур: прямоугольный треугольник, прямоугольник, круг; сечений составленных из простых фигур и стандартных профилей проката.
Элементы кинематики и динамики
Тема 2.1.6. Кинематика точки
Уравнение движения точки по заданной траектории. Скорость. Ускорение полное, нормальное, касательное. Виды движения точки в зависимости от ускорения. Равномерное движение точки.
Тема 2.1.7. Простейшие виды движения твердого тела
Поступательное движение твердого тела и его свойства. Вращательное движение твердого тела вокруг неподвижной оси. Угловое перемещение. Угловая скорость, угловое ускорение, частота вращения.
Линейные скорости точек вращающегося тела. Нормальное (центростремительное), касательное (тангенциальное) и полное ускорения точек вращающегося тела. Способы передачи вращательного движения. Понятие о передаточном отношении.
Тема 2.1.8. Плоскопараллельное (плоское) движение твердого тела
Разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг полюса.
Определение скоростей точек тела, совершающего плоское движение.
Тема 2.1.9. Сложное движение точки
Абсолютное, относительное и переносное движения точки. Теоремы о сложении скоростей и ускорений.
Тема 2.1.10. Элементы динамики точки
Основное уравнение динамики точки. Дифференциальные уравнения движения материальной точки в декартовых координатах. Основные теоремы динамики материальной точки (об изменении количества движения, момента количества движения, кинетической энергии).
Тема 2.1.11. Колебательное движение материальной точки.
Свободные колебания без учёта сил сопротивления. Свободные колебания при вязком сопротивлении. Вынужденные колебания. Резонанс.
Тема 2.1.12. Несвободное и относительное движение материальной точки.
Силы инерции. Принцип Даламбера. Дифференциальные уравнения движения несвободной материальной точки. Дифференциальные уравнения движения материальной точки в относительном движении. Динамическая теорема Кориолиса. Колебания маятника Дедуи.
Тема 2.1.13. Механическая система.
Дифференциальные уравнения движения механической системы. Основные теоремы динамики механической системы (теоремы об изменении количества движения, об изменении момента количества движения, об изменении кинетической энергии, о движении центра масс, теоремы сохранения).
Тема 2.1.14. Геометрия масс.
Масса система, движение центра масс. Момент инерции тела относительно оси и относительно точки. Центробежные моменты инерции. Теорема о параллельном переносе осей. Моменты инерции простейших однородных тел: однородный стержень, прямоугольная пластина, круглый цилиндр, шар.
Тема 2.1.15. Уравнения простейших движений механической системы.
Дифференциальные уравнения поступательного движения механической системы. Дифференциальные уравнения вращательного движения механической системы. Дифференциальные уравнения плоско-параллельного движения механической системы.
Тема 2.1.16. Элементарная теория гироскопов.
Кинетический момент тела, вращающегося вокруг неподвижной точки. Кинетическая энергия тела, вращающегося вокруг неподвижной точки. Динамические уравнения Эйлера. Астатический гироскоп. Гироскопический момент.
Тема 2.1.17. Связи.
Классификация механических связей. Возможные положения, скорость, ускорения системы. Возможные и действительные перемещения. Обобщённые координаты. Число степеней свободы. Возможная работа. Обобщённые силы. Идеальные связи.
Тема 2.1.18. Теория удара.
Линия удара. Прямой удар. Основные теоремы теории удара (теорема об изменении количества движения системы, теорема об изменении момента количества движения системы, теорема об изменении кинетической энергии механической системы, теорема о движении центра масс механической системы). Центр удара.
Тема 2.1.19. Элементы аналитической механики
Принцип возможных перемещений и общее уравнение динамики. Дифференциальные уравнения механической системы в обобщённых координатах. Уравнения Лагранжа 2 рода.
ЗАДАЧИ К КОНТРОЛЬНОЙ РАБОТЕ
I. СТАТИКА
Задача 1.1. Центр тяжести тел и фигур
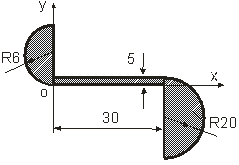
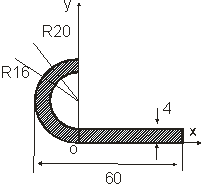
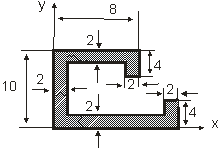
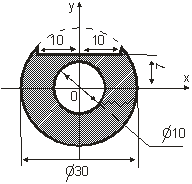
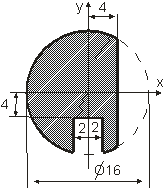
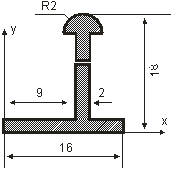
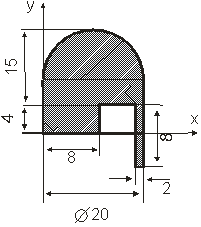
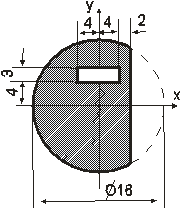
Определить координаты центра тяжести сложной тонкой однородной пластины (табл. 1.1).
Таблица 1.1
Вариант | Пластина | Вариант | Пластина |
1 |
| 2 |
|
3 |
| 4 |
|
5 |
| 6 |
|
7 |
| 8 |
|
9 |
| 0 |
|
Дополнительные сведения
1. Центр тяжести однородной плоской пластины
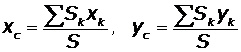 , (1.1)
, (1.1)
где S – площадь фигуры.
2. Центр тяжести площади треугольника – точка пересечения медиан:
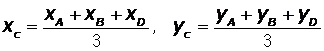 , (1.2)
, (1.2)
где xA, xВ, xD, yA, yВ, yD – координаты вершин треугольника в выбранной системе координат.
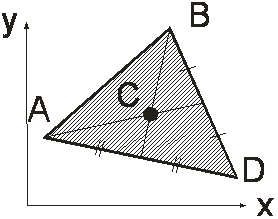
Рис 1.2. Центр тяжести площади треугольника
3. Центр тяжести дуги окружности лежит на оси симметрии Ох:
![]() , (1.3)
, (1.3)
где R – радиус дуги окружности, α – половина центрального угла в радианах.
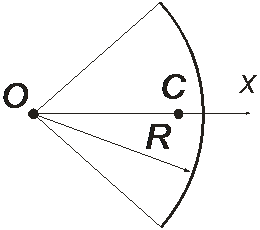
Рис. 1.3. Центр тяжести дуги лежит на оси симметрии
4. Центр тяжести площади кругового сектора лежит на оси симметрии Ох:
![]() , (1.4)
, (1.4)
где R – радиус сектора, α – половина центрального угла в радианах.
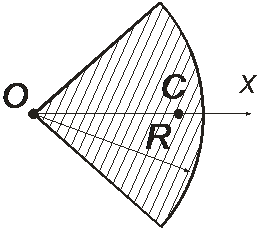
Рис. 1.4. Центр тяжести кругового сектора
Пример выполнения задания
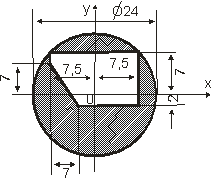
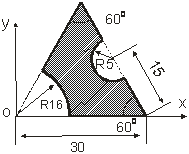
Определить координаты центра тяжести сложной тонкой однородной пластины, изображённой на рисунке 1.1, если OB = ОА = ОЕ = OF = 30 см, r = 30 см, OB1=R = 60 см.
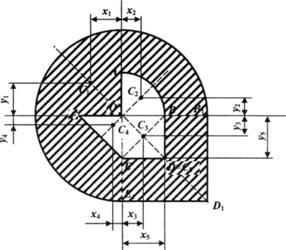
Рис. 1.5. Расчётная схема примера
Для решения задачи применяется метод дополнений. Разбиваем пластину на простейшие фигуры, центры тяжести которых можно вычислить:
1. сектор ОЕ1В1;
2. сектор ОАВ;
3. прямоугольник ОВДЕ;
4. треугольник OEF;
5. прямоугольник OB1D1E1.
Вычисляем площади (Sk) выделенных фигур:
![]() ,
, 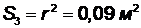 ,
,
![]() ,
, 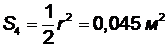 ,
,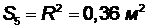 .
.
Используя формулу (1.4), определяем расстояния ОС1, ОС2 и координаты точек С1, С2:
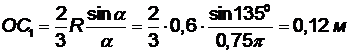 ,
,
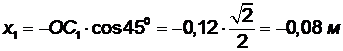 , y1 = OC1·cos 450=0,08 м,
, y1 = OC1·cos 450=0,08 м,
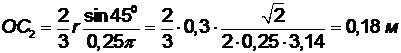 ,
,
x2 = y2 = OC2·cos 450=0,12 м.
Координаты точки С3: x3 = 0,15 м, у3 = - 0,15 м.
Координаты точки С4 определяются по формуле (1.2)
x4 = - 0,1 м, y4 = - 0,1 м.
Координаты точки С5 (совпадает с точкой D)
х5 = 0,3 м, у5 = - 0,3 м.
Координаты центра тяжести всей пластины определяются по формулам (1.1)
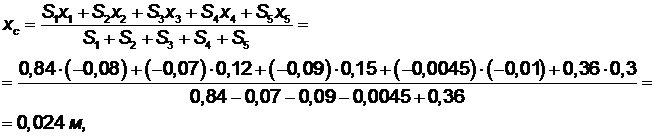
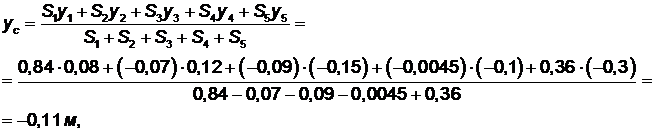
Ответ, xc = 0,024 м, ус = - 0,11 м.
Задача 1.2. Определение реакции опор твёрдого тела
Таблица 1.2
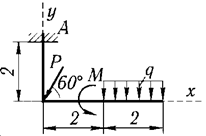
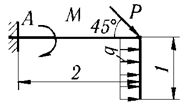
Вариант | Данные варианта | Схема варианта |
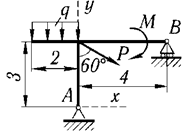
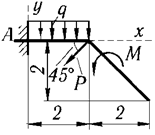
1 | Р = 10 кН, М = 6 кН·м, q = 2 кН/м |
|
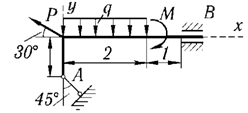
2 | P = 20 кН, М = 5 кН·м, q = 2 кН/м |
|
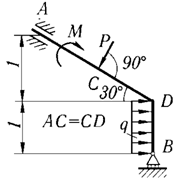
3 | P = 15 кН, М = 8 кН·м, q = 1 кН/м |
|
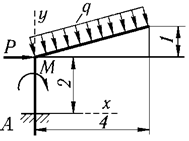
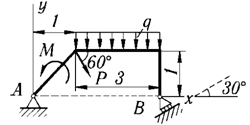
4 | P = 5 кН, M = 2 кН·м, q = 1 кН/м |
|
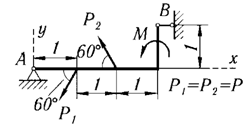
5 | P = 10 кН, М = 4 кН·м, P1 = P2 = P |
|
6 | P = 6 кН, M = 2 кН·м, q = 1 кН/м |
|
7 | P = 2 кН, M = 4 кН·м, q = 2 кН/м |
|
8 | P = 20 кН, М = 10 Кн·м, q = 4 кН/м |
|
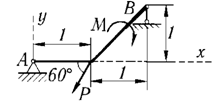
9 | P = 10 кН, M = 6 кН·м |
|
0 | P = 2 кН, M = 4 кН·м, q = 2 кН/м |
|
Образец выполнения задания
Д а н о: схема закрепления бруса
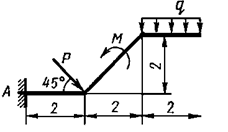
Рис. 1.6. Схема примера
P = 5 кН; M = 8 кН·м; q = 1,2 кН/м. Определить реакции опор.
Решение. Рассмотрим систему уравновешивающих сил, приложенных к конструкции. Действие связей на конструкцию заменим их реакциями (рис. 1.7). Равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей Q = q·2 = 2,4 кН.
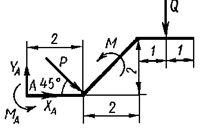
Рис. 1.7. Расчётная схема примера
Составим таблицу 1.3 проекций сил и моментов
Таблица 1.3
Силы | XA | YA | P | Q | M | MA |
Проекция на ось Ох | XA | 0 | P·cos450 | 0 | – | – |
Проекция на ось Оy | 0 | YA | P·sin450 | - Q | – | – |
Момент относительно точки А | 0 | 0 | - P·sin450·2 | - Q·5 | M | MA |
После составления таблицы проекций и моментов легко составить уравнения равновесия
XA + P·cos 45° = 0, (1.5)
YA + P·sin 45° − Q = 0, (1.6)
- P·sin 45°·2 − Q·5 + M + MA = 0. (1.7)
Из уравнения (1.5) находим XA = − P·cos 45° = −2,5·![]() .
.
Из уравнения (1.6) находим YA = − P·sin 45° + Q = −2,5·![]() + 2,4 ≈ − 1,14.
+ 2,4 ≈ − 1,14.
Из уравнения (1.7) находим MA = − M + Q·5 + P·sin 45°·2 ≈ 11,1.
II. КИНЕМАТИКА
Задача 2.1. Определение скорости и ускорения точки по заданным уравнениям её движения
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в таблице (2.1).
Таблица 2.1
Данные для решения задачи 2.1
Номер варианта | Уравнения движения | t1, c | |
х = x(t), см | y = y(t), см | ||
1 | -2 t2 + 3 | - 5t | 1/2 |
2 | 4 cos2 (π t /3) + 2 | 4 sin2 (π t /3) | 1 |
3 | - cos (π t 2/3) + 3 | sin (π t 2/3) - 1 | 1 |
4 | 4 t + 4 | - 4/(t + l) | 2 |
5 | 2 sin (π t/3) | - 3 cos(π t/3) +4 | 1 |
6 | 3 t2 + 2 | - 4 t | 1/2 |
7 | 3 t2 - t + 1 | 5 t2 - 5 t/3 - 2 | 1 |
8 | 7 sin (π t 2/6) + 3 | 2 -7 cos (π t 2/6) | 1 |
9 | -3/(t + 2) | 3t + 6 | 2 |
0 | - 4 cos (π t /3) | - 2 sin (π t /3) - 3 | 1 |
Образец выполнения задачи 2.1
По заданным уравнениям движения точки М
x = 4 sin t, y = 3 cos 2t (2.1)
установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение. Найдем траекторию движения, для этого необходимо из закона движения (2.1) исключить время
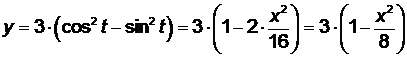 . (2.2)
. (2.2)
Как видно, траектория точки (2.2) это часть параболы, заключённой в прямоугольнике – 4 ≤ x ≤ 4, - 3 ≤ y ≤ 3.
Определим положение точки на траектории. Для этого необходимо подставить t = 1 сек. в закон движения (2.1)
x (1) = 4·sin 1 = 3,37 м; y (1) = 3·cos2 = - 1,25 м.
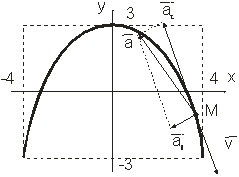
Рис. 2.1. Траектория, скорость, ускорение точки
Получим проекции скорости на оси координат
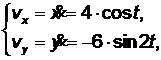 (2.3)
(2.3)
Найдём значения проекции скорости на оси координат в момент времени t = 1 сек., и по заданным проекциям скорости (2.3) найдём величину скорости
![]() .
.
Получим проекции ускорения на оси координат
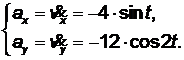 (2.4)
(2.4)
Найдём значения проекции ускорения на оси координат в момент времени t = 1 сек., и по заданным проекциям ускорения (2.4) найдём величину ускорения
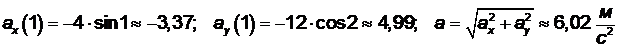 .
.
Поскольку точка описывает криволинейную траекторию, то её ускорение можно представить в виде векторной суммы двух составляющих ![]() , где
, где ![]() - касательное ускорение,
- касательное ускорение, ![]() - нормальное ускорение. Вектор
- нормальное ускорение. Вектор ![]() направлен по касательной, то есть по одной линии со скоростью и равен по величине проекции вектора ускорения на вектор скорости. Вектор
направлен по касательной, то есть по одной линии со скоростью и равен по величине проекции вектора ускорения на вектор скорости. Вектор ![]() направлен по главной нормали (перпендикулярно касательной) в сторону вогнутости траектории.
направлен по главной нормали (перпендикулярно касательной) в сторону вогнутости траектории.
Найдём касательное ускорение точки
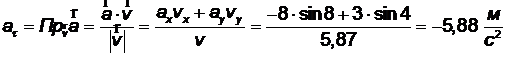 .
.
В данном случае направления векторов ![]() и
и ![]() противоположны и движение замедленное.
противоположны и движение замедленное.
Так как векторы ![]() и
и ![]() всегда взаимно перпендикулярны то модуль полного ускорения
всегда взаимно перпендикулярны то модуль полного ускорения ![]() . Отсюда найдём нормальное ускорение точки
. Отсюда найдём нормальное ускорение точки
![]() .
.
Радиус кривизны траектории определим из формулы для нормального ускорения 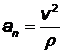 , откуда в момент времени t = 1 сек. будем иметь
, откуда в момент времени t = 1 сек. будем иметь
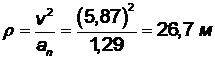 .
.
III. ДИНАМИКА
Задача 3.1. Динамика материальной точки
Силы, заданные формулами, измеряют в Н.
1. По шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом, опускается без начальной скорости тело. Определить, в течение какого времени тело опустится на высоту h = 10 м по вертикали, если коэффициент трения скольжения f = 0,1.
2. На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси х, действует сила, проекция которой равна Fх = 0,25 m x. В начальный момент тело находилось в покое в точке xo = 1 м. Определить скорость тела в момент, когда координата станет равной х = 5 м.
3. Сила тяги винтов вертолета массой m при его вертикальном подъеме из состояния покоя в 1,5 раза превышает его вес. Сопротивление воздуха пропорционально скорости ![]() . Определить скорость подъема в момент t = 5 с, а также максимальную скорость вертолета.
. Определить скорость подъема в момент t = 5 с, а также максимальную скорость вертолета.
4. Лодке массой m = 100 кг сообщается начальная скорость vo = 4 м/с. При движении на лодку действует сила сопротивления, пропорциональная квадрату скорости R = 5 v2. Определить, в течение какого времени скорость лодки уменьшится в два раза.
5. Телу сообщается начальная скорость v0 = 6,6 м/с, и оно начинает скользить вверх по шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом. Коэффициент трения скольжения f = 0,2. Определить время достижения наивысшего положения тела и пройденный телом за это время путь.
6. На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси х, действует сила, проекция которой равна Fх = − 0,36 m x. В начальный момент х0 = 0 и проекция скорости Vxo = 3 м/с. Определить максимальное значение координаты х тела.
7. Груз массой m = 10 кг опускается вертикально на парашюте без начальной скорости. Сопротивление воздуха пропорционально скорости 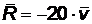 . Определить скорость груза в момент времени t = 1 с.
. Определить скорость груза в момент времени t = 1 с.
8. В момент выключения мотора катер массой m = 200 кг имел скорость. Определить путь, который пройдет катер до того момента времени, когда скорость катера уменьшится в десять раз. Сила сопротивления движению пропорциональна квадрату скорости R = 8 v2.
9. Тело начинает скользить вниз по шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом, с начальной скоростью vo = 2 м/с. Коэффициент трения скольжения f = 0,4. Определить путь, пройденный телом за время t = 2с.
0. Материальная точка массой m = 2 кг движется из состояния покоя по горизонтальной гладкой поверхности вдоль оси х под действием силы, проекция которой равна Fх = 3 (1 − 0,5 t ). Определить скорость и координату точки в тот момент времени, когда сила станет равной нулю. Начальную координату точки считать нулевой.
Образец выполнения задачи 3.1
Тело массой m = 15 кг поднимается по гладкой наклонной плоскости, составляющей угол α = 30°с горизонтом, получив начальную скорость v0 = 10 м/с. Сопротивление среды пропорционально скорости 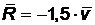 . Определить время, прошедшее до остановки тела.
. Определить время, прошедшее до остановки тела.
Решение. Изобразим тело на наклонной плоскости (рис. 3.1)
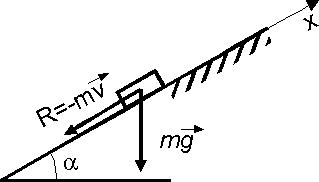
Рис. 3.1. Рисунок к задаче 3.1
Составим уравнения движения тела в проекции на ось Ох
![]() (3.1)
(3.1)
Уравнение (3.1) можно записать в виде
![]() (3.2)
(3.2)
Уравнение (3.2) является линейным дифференциальным уравнением первого порядка с разделяющимися переменными. Представим производную от скорости как отношение дифференциалов функции и независимой переменной
![]()
и проведём разделение переменных
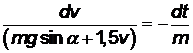 . (3.3)
. (3.3)
Проинтегрируем соотношение (3.3)
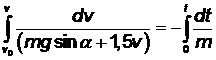 . (3.4)
. (3.4)
Используя свойства дифференциала и определённого интеграла, выполним замену аргумента интегрирования в левой части
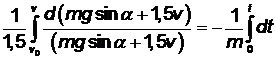 (3.5)
(3.5)
Интегралы в левой и правой части соотношения (3.5) являются табличными и по формуле Ньютона – Лейбница получим
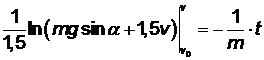
или
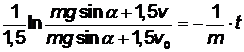 . (3.6)
. (3.6)
Пусть t = T время, при котором v = 0. Из соотношения (3.6) получим
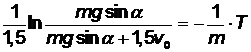 ,
,
откуда находим время, за которое тело остановится
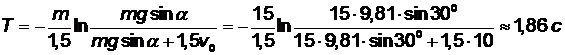 .
.
Ответ: 0,86 с.
Задача 3.2. Элементарная теория удара
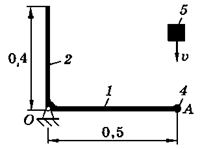
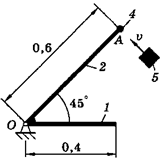
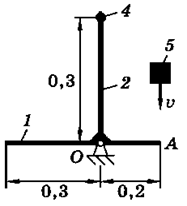
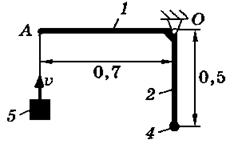
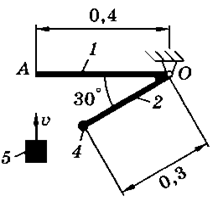
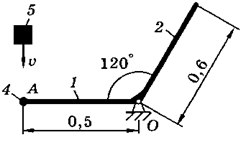
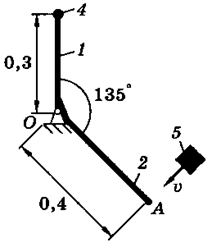
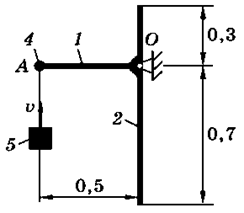
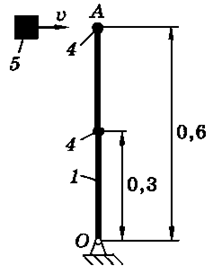
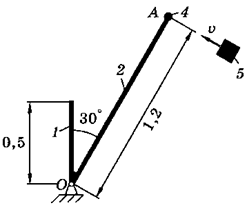
На схемах (таблица 3.2) показаны механические системы, состоящие из конструкции и ударяющего по ней тела. Конструкция может вращаться вокруг оси, проходящей через неподвижную точку О. Она состоит из тонких однородных стержней 1 и 2, или однородной пластины 3 и точечных грузов 4. Масса 1 м длины стержней равна 25 кг, масса 1 м2 площади пластины - 50 кг, масса точечного груза - 20 кг. Размеры частей конструкции указаны в метрах.
Тело 5 (материальная точка) массой m5 = 30 кг, двигаясь со скоростью v = 4 м/с, ударяется о неподвижную конструкцию в точке А, причем удар является абсолютно неупругим.
Определить угловую скорость конструкции после удара и воспринимаемый ею ударный импульс. Найти также потерянную при ударе кинетическую энергию системы.
Таблица 3.2
Вариант | Схема | Вариант | Схема |
1 |
| 2 |
|
3 |
| 4 |
|
5 |
| 6 |
|
7 |
| 8 |
|
9 |
| 0 |
|
Образец выполнения задачи 3.2
Груз массой m1 = 10 кг, двигаясь поступательно со скоростью v = 5 м/с по горизонтальной поверхности, сталкивается с нижним концом висящего вертикально однородного стержня массой m2 = 30 кг и длиной I = 0,5 м (рис. 1). Считая удар абсолютно неупругим, определить угловую скорость стержня w и скорость груза после удара v, а также величины действующих ударных импульсов. Найти также потерянную при ударе кинетическую энергию системы.
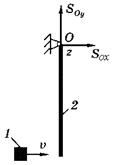
Рис. 3.1. Схема задачи
Решение. Если в качестве механической системы рассматривать груз и стержень, то возникающая между ними ударная сила окажется силой внутренней (ударный импульс ![]() ), а внешним ударным будет лишь импульс на оси вращения стержня, который разложим на составляющие
), а внешним ударным будет лишь импульс на оси вращения стержня, который разложим на составляющие ![]() ох и
ох и ![]() oy.
oy.
Применим к системе теорему об изменении кинетического момента при ударе относительно оси вращения стержня z:
![]()
В данном случае
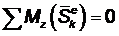
и кинетический момент системы в процессе удара сохранится: Kz = (Kz)0.
До удара стержень был неподвижен и кинетический момент был лишь у груза (момент его количества движения ![]() ): (Кz)0 =m1v l.
): (Кz)0 =m1v l.
После удара скорость груза изменится и станет равной некоторой величине u, а стержень приобретет некоторую угловую скорость ω и кинетический момент Jzω, где
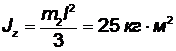
— осевой момент инерции стержня. Таким образом, после удара
Кz = m1 u l + Jzω.
Поскольку удар является абсолютно неупругим (т. е. отсутствует отскок), то и = ω l, тогда
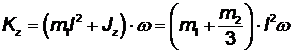
Приравнивая кинетические моменты до удара и после него, получаем
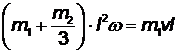 , откуда
, откуда 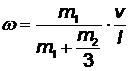 .
.
Скорость груза после удара u = ω l = 2,5 м/с.
Для вычисления ударного импульса S между грузом и стержнем
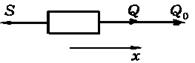
Рис.3.2. Импульсы взаимодействия груза
применим к грузу (рис. 2) теорему об изменении количества движения при ударе 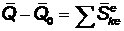 .
.
В проекции на горизонтальную ось имеем т1 и - т1 v = - S, откуда S = т1 (v - и) = 25 Н c.
Чтобы вычислить ударные импульсы на оси стержня, применим к нему теорему об изменении количества движения при ударе, учитывая, что количество движения тела равно произведению его массы на скорость центра масс (рис. 3).
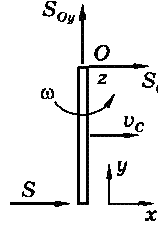
Рис. 3.3. Импульсы взаимодействия груза и стержня
До удара стержень был неподвижен и (Qо = 0, после удара Q = m2vc, где
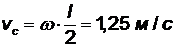
В проекции на ось х теорема дает т2vc - 0 = S + S0х> откуда S0х = т2vc - S = 12,5 Н × c.
Проекции на ось у количества движения стержня до и после удара нулевые, и тогда из теоремы легко видеть, что S0у = 0.
Таким образом, ударный импульс на оси стержня So = S0х = 12,5 Н × c.
Определим потерянную в процессе удара кинетическую энергию. До удара двигался только груз и его кинетическая энергия была
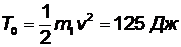
После удара двигались и груз, и стержень; общую кинетическую энергию системы находим
![]() .
.
Таким образом, потерянная кинетическая энергия Т0 - Т = 62,5 Дж.
Последний результат можно было получить иначе, используя теорему Карно: потеря кинетической энергии при абсолютно неупругом ударе равна кинетической энергии потерянных скоростей 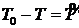 . Для груза потерянная скорость равна v - и, для стержня потерянная угловая скорость равна 0 - w = - w, и тогда
. Для груза потерянная скорость равна v - и, для стержня потерянная угловая скорость равна 0 - w = - w, и тогда
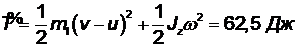 .
.
Потерянная кинетическая энергия переходит в тепло и необратимые деформации.
Ответ: w = 5 с-1; и = 2,5 м/с; S = 25 Н×c; S0 = 12,5 Н×c; Т0 - Т = 62,5 Дж.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Тарг, курс теоретической механики/ . – М.: Высшая школа, 2004.
2. Бать, механика в примерах и хадачах/ [и др. ]. – М.: Наука, 1973. – Т. 1, 2, 3.
3. Дорожкина, заданий по теоретической механике. Статика/ [и др. ]. – СПб.: Лань, 2012.
4. Диевский, механика. Сборник заданий/ , . – СПб.: Лань, 2009.