Корневые векторы и корневые подпространства. Терема об инвариантности корневого подпространства. Теорема о прямой сумме корневых подпространств. Линейная независимость корневых векторов. Теорема о разложении пространства в прямую сумму корневых подпространств.
Def 1. Ненулевой вектор ![]() , называется корневым вектором линейного оператора
, называется корневым вектором линейного оператора ![]() , соответствующим числу
, соответствующим числу ![]() , если существует натуральное
, если существует натуральное ![]() , такое, что выполняется равенство
, такое, что выполняется равенство 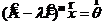 . Минимальное
. Минимальное ![]() для которого справедливо это равенство называется высотой вектора
для которого справедливо это равенство называется высотой вектора ![]() .
.
Рассмотрим подпространство - линейную оболочку всех таких векторов ![]() , для которых справедливо равенство
, для которых справедливо равенство 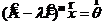 . Тогда справедлива:
. Тогда справедлива:
Лемма. (Подпространство ![]() отлично от нулевого вектора)
отлично от нулевого вектора) ![]() (
( ![]() - собственное значение оператора
- собственное значение оператора ![]() ).
).
Доказательство. Если ![]() - собственное значение, то существует собственный вектор
- собственное значение, то существует собственный вектор ![]() , такой, что
, такой, что ![]() , т. е.
, т. е. ![]() . Если подпространство
. Если подпространство ![]() содержит ненулевой вектор
содержит ненулевой вектор ![]() , то пусть
, то пусть ![]() - наименьшее натуральное число, такое, что
- наименьшее натуральное число, такое, что 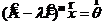 , тогда
, тогда 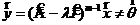 . Но тогда
. Но тогда 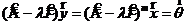 , следовательно
, следовательно ![]() - собственный вектор оператора
- собственный вектор оператора ![]() , а
, а ![]() - его собственное значение.#
- его собственное значение.#
Отсюда, в частности, следует, что собственный вектор линейного оператора является корневым высоты 1 ( ).
По аналогии с собственным вектором говорят, что корневой вектор ![]() принадлежит собственному значению
принадлежит собственному значению ![]() .
.
Поэтому можно дать следующее определение.
Обозначим ={ ![]() :
: ![]() - корневой вектор оператора принадлежащий собственному значению
- корневой вектор оператора принадлежащий собственному значению ![]() или
или ![]() }.
}.
Теорема 1. (О корневом подпространстве). Множество ![]() :
:
1) Является подпространством;
2) Это подпространство инвариантно относительно любого оператора ![]() , где
, где ![]() принадлежит основному полю К.
принадлежит основному полю К.
Доказательство. 1) a. ![]() по построению множества
по построению множества
b. Если 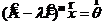 , то
, то 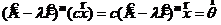 . Значит если
. Значит если ![]() то и
то и ![]()
c. Если 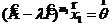 и
и 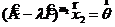 , то выбрав в качестве
, то выбрав в качестве
получаем ![]() . Значит если
. Значит если ![]()
![]() то и
то и 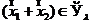 .
.
То есть множество ![]() является подпространством.
является подпространством.
2) Возьмём 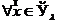 , т. е.
, т. е. 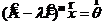 обозначим
обозначим 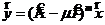 .
.
Воспользовавшись очевидным тождеством 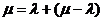 имеем:
имеем:
![]() .
.
Следовательно ![]() и значит
и значит ![]() . Инвариантность доказана.
. Инвариантность доказана.
Эта теорема позволяет так сформулировать (эквивалентное) определение корневого подпространства ![]() .
.
Def 2. Линейная оболочка корневых векторов, соответствующих собственному числу ![]() , называется корневым подпространством, соответствующим собственному числу
, называется корневым подпространством, соответствующим собственному числу ![]() .
.
Def. 2а. Пусть дан оператор 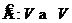 . Корневым подпространством, отвечающим собственному числу
. Корневым подпространством, отвечающим собственному числу ![]() оператора
оператора ![]() называется множество
называется множество ![]() , состоящее из векторов
, состоящее из векторов ![]() , для которых существует такое натуральное число
, для которых существует такое натуральное число ![]() , что
, что 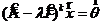 .
.
Таким образом: ![]() . Если - собственные векторы оператора , то им соответствующие корневые подпространства обозначаются как
. Если - собственные векторы оператора , то им соответствующие корневые подпространства обозначаются как ![]() , т. е. собственному значению соответствует корневое подпространство
, т. е. собственному значению соответствует корневое подпространство ![]() , или сокращённо -
, или сокращённо - ![]() .
.
Def. 3. Пусть ![]() - подпространство
- подпространство ![]() инвариантное относительно линейного оператора
инвариантное относительно линейного оператора ![]() , т. е.
, т. е. 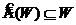 . В этом случае определён оператор
. В этом случае определён оператор ![]() , действующий по формуле
, действующий по формуле ![]() . Таким образом определённый оператор
. Таким образом определённый оператор ![]() называется ограничением (сужением) оператора
называется ограничением (сужением) оператора ![]() на инвариантное подпространство
на инвариантное подпространство ![]() . Говорят так же, что
. Говорят так же, что ![]() индуцирован оператором
индуцирован оператором ![]() .
.
Лемма 1. Если ![]() , то
, то ![]() .
.
(Другими словами, если ![]() и
и ![]() , то
, то ![]() при
при
Доказательство. Пусть ![]() , т. е.
, т. е. ![]() и
и ![]() . Тогда
. Тогда ![]() и следовательно
и следовательно ![]() , а т. к.
, а т. к. ![]() , то
, то ![]() . #
. #
Пусть ![]() различные собственные значения оператора
различные собственные значения оператора ![]() и
и ![]() - соответствующие корневые подпространства. Тогда справедлива следующая
- соответствующие корневые подпространства. Тогда справедлива следующая
Теорема 2. (О прямой сумме корневых подпространств). Сумма подпространств: ![]() является прямой суммой, т. е.
является прямой суммой, т. е.
Доказательство проведём индукцией по k. 1) При k=1 утверждение очевидно.
2) Пусть утверждение справедливо для (k-1) корневых подпространств и докажем его справедливость для k корневых подпространств. Так как ![]() , то
, то ![]() . Поэтому из
. Поэтому из ![]() следует,
следует, ![]() , где
, где ![]() . Так как корневые подпространства
. Так как корневые подпространства ![]() инвариантны относительно оператора
инвариантны относительно оператора ![]() , то
, то ![]() и по предположению индукции
и по предположению индукции 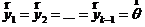 .
.
По лемме 1 из ![]() при
при ![]() следует, что
следует, что ![]() , а значит и
, а значит и ![]() . #
. #
Лемма 2 (О линейной независимости корневых векторов). Пусть 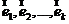 - корневые векторы принадлежащие одному собственному значению
- корневые векторы принадлежащие одному собственному значению ![]() , с попарно различными высотами
, с попарно различными высотами 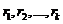 . Тогда
. Тогда 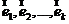 линейно независимы.
линейно независимы.
Доказательство проведём индукцией по k. Расположим корневые векторы в порядке возрастания их высот.
1) При k=1 утверждение леммы очевидно.
2) При k=2 имеем 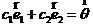 , возьмём
, возьмём 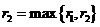 ,
, 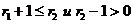 .
.
Тогда ![]() .
.
3) Пусть утверждение леммы справедливо для (k-1) и докажем его справедливость для k.
Рассмотрим равенство ![]() и
и ![]() ,
,
тогда ![]()
и по предположению индукции имеем 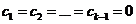 .#
.#
Теорема 3 (О разложении пространства в прямую сумму корневых подпространств). Пусть ![]() - все собственные значения линейного оператора
- все собственные значения линейного оператора ![]() с алгебраическими кратностями
с алгебраическими кратностями ![]() , соответственно
, соответственно ![]() , а
, а ![]() корневые подпространства. Тогда
корневые подпространства. Тогда ![]() и
и
Доказательство. Докажем, что ![]() . Действительно,
. Действительно, ![]() - инвариантное подпространство, возьмем
- инвариантное подпространство, возьмем ![]() базис в
базис в ![]() (
( ) и дополним его до базиса всего пространства
) и дополним его до базиса всего пространства ![]() :
: ![]() . Обозначим линейную оболочку
. Обозначим линейную оболочку ![]() - подпространство
- подпространство ![]() , тогда
, тогда ![]() и матрица оператора в базисе
и матрица оператора в базисе ![]() будет иметь вид
будет иметь вид
![]()
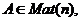
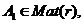
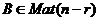 .
.
Характеристический многочлен оператора в этом случае можно представить в виде произведения двух многочленов степени r и (n-r), соответственно:  . Предположим, что
. Предположим, что ![]() , тогда
, тогда ![]() должен быть корнем характеристического уравнения
должен быть корнем характеристического уравнения 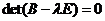 , т. е. собственным значением матрицы
, т. е. собственным значением матрицы ![]() . По матрице
. По матрице ![]() построим оператор
построим оператор ![]() - линейный оператор с матрицей
- линейный оператор с матрицей ![]() в базисе
в базисе ![]() . Тогда
. Тогда ![]() - собственное значение оператора
- собственное значение оператора ![]() и существует собственный вектор
и существует собственный вектор 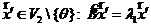 , при этом
, при этом 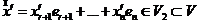 . Обозначим
. Обозначим 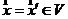 , причем
, причем 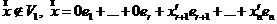 и запишем
и запишем 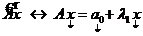 , причем:
, причем:  , т. е.
, т. е. 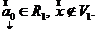
Тогда с одной стороны ![]() и
и ![]() , но (!):
, но (!):
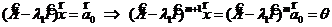 - противоречие. Это противоречие доказывает, что
- противоречие. Это противоречие доказывает, что ![]() . Тогда аналогично
. Тогда аналогично![]() Тогда
Тогда ![]() , а
, а ![]() , так как
, так как ![]() - подпространство
- подпространство ![]() . Отсюда получаем, что
. Отсюда получаем, что ![]() и
и ![]() , как подпространство, имеющее ту же размерность. #
, как подпространство, имеющее ту же размерность. #
Следствие. Максимальная высота корневого вектора, принадлежащего ![]() не превосходит
не превосходит ![]() .
.
Доказательство. Пусть ![]() с высотой
с высотой ![]() . Тогда векторы
. Тогда векторы ![]() - корневые векторы, принадлежащие
- корневые векторы, принадлежащие ![]() с попарно различными высотами
с попарно различными высотами 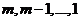 (по определению). Тогда по Лемме 2 они линейно независимы и их число
(по определению). Тогда по Лемме 2 они линейно независимы и их число ![]() штук. Это противоречит тому, что
штук. Это противоречит тому, что 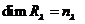 . #
. #
Способ нахождения корневых векторов:
1. Ищем собственные числа ![]()
2. Для каждого собственного числа ![]() решаем систему(мы) уравнений
решаем систему(мы) уравнений ![]() , где
, где ![]() - кратность корня
- кратность корня ![]() , как корня характеристического уравнения. Отсюда находим корневые векторы высоты
, как корня характеристического уравнения. Отсюда находим корневые векторы высоты ![]() .
.
Другое доказательство теоремы
Теорема 3а (О разложении пространства в прямую сумму корневых подпространств). Каков бы ни был линейный оператор ![]() комплексного пространства
комплексного пространства ![]() , это пространство раскладывается в прямую сумму инвариантных относительно оператора
, это пространство раскладывается в прямую сумму инвариантных относительно оператора![]() корневых подпространств.
корневых подпространств.
Для доказательства теоремы вначале разложим пространство в прямую сумму инвариантных подпространств, а затем докажем, что эти подпространства – корневые.
Лемма 3. Каков бы ни был линейный оператор ![]() комплексного пространства
комплексного пространства ![]() , это пространство раскладывается в прямую сумму инвариантных относительно оператора
, это пространство раскладывается в прямую сумму инвариантных относительно оператора![]() подпространств.
подпространств.
Доказательство. Пусть ![]() - n-мерное комплексное линейное пространство,
- n-мерное комплексное линейное пространство, ![]() - линейный оператор, имеющий в произвольном базисе
- линейный оператор, имеющий в произвольном базисе 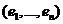 пространства V матрицу
пространства V матрицу ![]() . Характеристический многочлен оператора
. Характеристический многочлен оператора ![]() (матрицы
(матрицы ![]() )
) ![]() в комплексном пространстве раскладывается в общем виде на сомножители так:
в комплексном пространстве раскладывается в общем виде на сомножители так:
![]()
Замечание. В действительном пространстве такое разложение возможно в случае наличия у характеристического многочлена только действительных корней.
Рассмотрим рациональную функцию ![]() и разложим её на сумму элементарных дробей в виде:
и разложим её на сумму элементарных дробей в виде:
![]() .
.
После приведения к общему знаменателю из равенства числителей получается тождество: ![]() , где
, где ![]() - многочлен, равный произведению
- многочлен, равный произведению![]() на многочлен, получаемый из
на многочлен, получаемый из 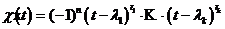 вычёркиванием множителя
вычёркиванием множителя ![]() :
: 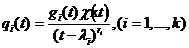 .
.
Подставив в полученное тождество, оператор ![]() вместо t, получим операторное равенство:
вместо t, получим операторное равенство:
![]() (*)
(*)
Операторы ![]() обладают следующим свойством:
обладают следующим свойством: 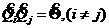 .
.
Действительно, в произведении ![]() содержатся все множители, содержащиеся в разложении
содержатся все множители, содержащиеся в разложении 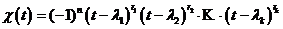 , и при подстановки оператора
, и при подстановки оператора ![]() вместо t это произведение станет аннулирующим. Умножая (*) на
вместо t это произведение станет аннулирующим. Умножая (*) на ![]() и используя свойство
и используя свойство ![]() получаем для любого i=1,2,…,k равенство
получаем для любого i=1,2,…,k равенство 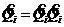 .
.
Теперь мы можем разложить пространство V прямую сумму. Действуем обеими частями операторного равенства (*) на произвольный вектор пространства V:
![]() (**)
(**)
или ![]() , где
, где ![]() .
.
Покажем, что разложение такого вида единственно. Действительно, допустим, что существует другое такое разложение: 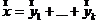 , где
, где ![]() ( i=1,2,…,k). Это значит, что найдутся такие векторы
( i=1,2,…,k). Это значит, что найдутся такие векторы ![]() , что
, что ![]() . Тогда действуя на обе части равенства
. Тогда действуя на обе части равенства  оператором
оператором ![]() , и используя свойства
, и используя свойства 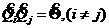 и
и ![]() , получаем
, получаем ![]() , т. е.
, т. е. ![]() . Единственность доказана.
. Единственность доказана.
Равенство (**) означает, что V является суммой подпространств ![]() , а единственность этого разложения равносильна тому, что сумма прямая:
, а единственность этого разложения равносильна тому, что сумма прямая:
![]() (***)
(***)
Подпространства ![]() инвариантны. Лемма 3 доказана.
инвариантны. Лемма 3 доказана.
Для завершения доказательства теоремы покажем, что построенные таким образом подпространства![]() суть корневые подпространства.
суть корневые подпространства.
Лемма 4.
Доказательство. В произведении ![]() входят все множители, составляющие характеристический многочлен
входят все множители, составляющие характеристический многочлен ![]() оператора
оператора ![]() . Поэтому из теоремы Гамильтона-Кэли следует, что
. Поэтому из теоремы Гамильтона-Кэли следует, что 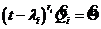 .
.
Это означает, что для любого ![]() выполнено
выполнено ![]() , т. е.
, т. е. ![]() , что равносильно включению
, что равносильно включению ![]() .
.
С другой стороны, пусть ![]() . В каждом прообразе оператора
. В каждом прообразе оператора ![]() при
при ![]() входит множитель
входит множитель ![]() , обращающий в нулевой вектор
, обращающий в нулевой вектор ![]() .
.
Поэтому формула (**)![]() для такого имеет вид
для такого имеет вид ![]() . Значит,
. Значит, ![]() , поэтому справедливо и включение
, поэтому справедливо и включение ![]() . #
. #
Таким образом мы доказали, что пространство ![]() раскладывается в прямую сумму подпространств инвариантных относительно оператора
раскладывается в прямую сумму подпространств инвариантных относительно оператора![]() , являющихся его корневыми подпространствами
, являющихся его корневыми подпространствами ![]() .#
.#



