Тест №3 .
«Формула полной вероятности. Теорема гипотез (формула Байеса)»
Если событие А может наступить только с одним из n попарно несовместных событий H1, H2,..., Hn, которые по отношению к А называются гипотезами, тогда вероятность события А можно вычислить по формуле полной вероятности:
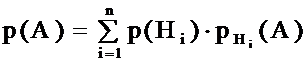
Если вероятность p(A) вычислена по этой формуле, то вероятности гипотез p(Hi) можно переоценить, т. е. найти условные вероятности pA(Hi) по формуле Байеса:
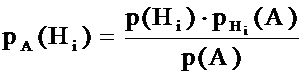
1. Пять экзаменаторов принимают экзамен по предмету. Известно, что вероятность сдать экзамен двум из них равна 0,6, а трем остальным 0,8.
а) вероятность сдать экзамен произвольному экзаменатору
составляет....
1) 0,48 2) 0,72 3) 0,28 4) 0,7
б) Студент экзамен сдал, т. е. есть ответ по пункту а. Вероятность того,
что он сдавал экзамен тем преподавателям, у которых вероятность
сдачи равна 0,8 составляет....
1) 2/3 2) 1/2 3) 4/5
2. Имеются три коробки с шарами. В первой - 4 белых и 5 черных шаров, во второй - 5 белых и 4 черных шара, в третьей - 6 белых шаров. Наугад из какой-то одной коробки вынимают один шар. Вероятность того, что:
а) Этот шар окажется белым, составляет…
1) 2/3 2) 1/3 3) 5/6
б) Этот белый шар вынут из второй коробки, составляет…
1) 0,,,578
3. В пирамиде 10 винтовок, из которых 4 с оптическим прицелом. Вероятность попасть в цель из обычной винтовки равна 0,8, а с оптическим прицелом равна 0,95. Стрелок взял винтовку наудачу и поразил цель. Более вероятно, что он стрелял из винтовки....
1) с оптическим прицелом;
2) без оптического прицела.
4. В школе 60% - девочки. Билеты в театр имеют 80% девочек и 75%
мальчиков. Кто-то потерял билет. Вероятность того, что этот билет
принадлежал...
а) девочке, составляет....
1) 5/13 2) 8/13 3) 5/26
б) мальчику, составляет....
1) 5/13 2) 8/13 3) 5/26
5. Партия деталей 50 шт предоставлена тремя поставщиками: 1-ый поставил – 20 шт; 2-ой– 25 шт; 3-ий - 5 шт. Вероятности брака: у 1-го - 0,02; у 2-го - 0,01; у 3-го - 0,05 - это априорные (заявленные) вероятности. Все детали смешали.
а) Вероятность того, что взятая наугад одна деталь окажется бракованной, составляет…
1) 0,,,946
б) Наиболее вероятно, что эта бракованная деталь выпущена заводом…
1) 1-ым 2) 2-ым 3) 3-им.
Тест № | Пояснение | Ответ |
1. | Событие А - экзамен сдан а) По формуле полной вероятности:
| 0,72 |
б) По формуле переоценки гипотез:
| 2/3 | |
2. |
Событие А - вынут белый шар. Вероятность этого:
| 2/3 |
б) Вероятность того, что этот белый шар вынут из второй коробки (по формуле Байеса): | 0,278 | |
3. | H1 - попалась винтовка с оптическим прицелом; p(H1)=0,4. H2 - попалась обычная винтовка; p(H2)=0,6 По условию: Вероятность того, что попали в цель: р(А) =0,4·0,95 + 0,6·0,8=0,38 + 0,48=0,86 По формуле Байеса оценим вероятности гипотез:
т. е. белее вероятно, что стреляли из обычной винтовки без оптического прицела. | Без оптического прицела |
4. | Имеются две гипотезы: девочка: p(H1)=0,6 ; мальчик: p(H2)=1-0,6=0,4 Вероятность того, что билет: потеряла девочка: потерял мальчик: Полная вероятность: Переоценим гипотезы: а) Потеряла девочка: | 8/13 (0,615) |
б) Потерял мальчик: Наиболее вероятно, что билет потеряла девочка | 5/13 (0,385) | |
5. | а) Пусть событие (А) – взятая наугад деталь – бракованная. Имеются три гипотезы: Н1 – деталь выпущена 1-ым заводом Н2 – деталь выпущена 2-ым заводом Н3 – деталь выпущена 3-им заводом Тогда вероятности того, что попалась деталь соответствующего завода (вероятности гипотез):
По условию: Тогда искомая вероятность события А:
| 0,018 |
б) Требуется переоценить гипотезы при p(A)=0,018. По формуле Байеса получаем:
Наиболее вероятно, что взятая бракованная деталь 1-го завода. | 1-го завода |




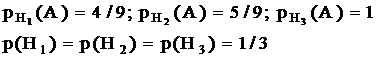
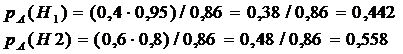
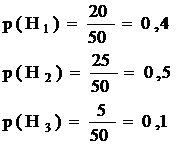
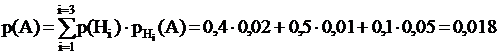
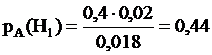 (было 0,4)
(было 0,4)