Прогнозирование пассажирских перевозок на основе обработки временных рядов (стр. 2 )

·  Вычисляются теоретические уровни ряда в каждый момент времени по соответствующему полиному, характеризующему тренд (в данном примере используется линейный тренд на рис.1, параметры которого определены по методу наименьших квадратов);

·  Определяется отношение фактических данных () к выравненным данным () для каждого месяца (индекс сезонности по месяцам)

;

·  Находятся средние из соотношений, рассчитанных по одноименным периодам (индекс сезонности по одноименным периодам)

, где n – число одноименных периодов. Проверка правильности вычисления индексов. Средний индекс сезонности для всех месяцев должен быть равен 1, т. к. сезонные колебания взаимопогашаются в течение года.

В табл. 2 приведены расчеты по методу выравнивания по прямой.

Таблица 2

В табл. 3 приведены окончательные значения мультипликативных сезонных индексов для исходного ряда, полученные после процедуры сглаживания методом скользящих средних.

Таблица 3

На рис. 2 приведен исходный ряд и уравнение тренда после выделения сезонной компоненты.

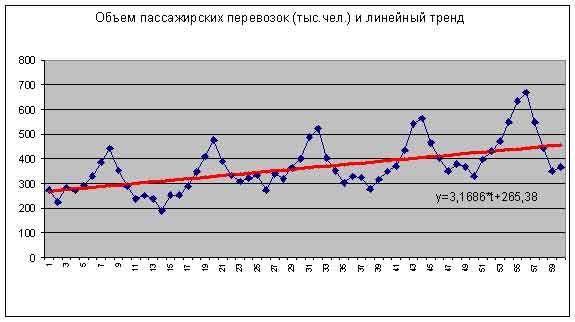
Рис.2 Уравнение тренда без сезонной компоненты

Очевидно, что значения составляющих временного ряда находятся в зависимости от последовательности и методов их выделения.

Если выбранная для прогнозирования кривая не является единственной для описания тенденции, то для каждого уравнения тренда рассчитывается коэффициент детерминации (R2), F-критерий Фишера, а также критерий Дарбина-Уотсона. Чем выше R2, тем выше вероятность того, что временной ряд описывается данным уравнением тренда. Влияние случайного фактора оценивается как (1- R2). В нашем примере R2 для линейного уравнения тренда равен 0,9506. Если для описания тенденции исходного ряда использовалась бы парабола, то R2 равнялся бы 0,9589. Очевидно, что при описании временного ряда предпочтение следует отдавать параболическому тренду.

Критерий Дарбина-Уотсона оценивает автокорреляцию остатков. Если автокорреляция в остатках отсутствует, то уравнение пригодно для прогноза[2].

При выборе уравнения тренда можно использовать среднюю ошибку аппроксимации, которая определяется по формуле:

.

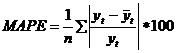Для нашего примера с линейным трендом средняя ошибка аппроксимации составила 5,5%. Если средняя ошибка не превысила 5-7%, уравнение тренда хорошо подходит для описания тенденции временного ряда.

В приведенном примере при прогнозировании используется сравнительно небольшая глубина исходной статистики. По мере накопления статистической информации вид тренда, используемый для прогнозирования, может изменяться.

Прогнозирование объемов пассажирских перевозок может производиться по различным уровням агрегации данных: как на уровне авиакомпании в целом, так и на уровне отдельных регионов, рейсов и направлений.

Задача прогнозирования объёмов пассажирских перевозок является основой для решения многих задач оптимизации воздушно-транспортной системы по критериям, непосредственно связанным с показателем рентабельности (доходы, затраты, прибыль), поскольку оптимальность планов, получаемых при решении этих задач, зависит прежде всего от точности прогнозов.

Литература:

1. “Прогнозирование пассажирских перевозок”. В книге”Наука и техника гражданской авиации”, ВИНИТИ, М, 1975.

2. , ” Прогнозирование пассажирских перевозок”, М, Транспорт,1980

Из за большого объема этот материал размещен на нескольких страницах: 1 2