АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ
ГОРОДА ДОЛГОПРУДНОГО
ЛИЦЕЙ №11 «ФИЗТЕХ»
XII научно-практическая конференция
Старт в инновации
Изучение особенностей движения тел в поле тяжести Земли
Авторы работы: Савлаев Руслан, 7 класс,
Серебряков Никита, 7 класс,
Русс Тимофей, 7 класс,
Бажин Егор, 7 класс,
Научный руководитель: ,
к. ф.-м. н., преподаватель МФТИ
2012 г.
Оглавление
1. Введение 3
2. Теоретические основы механики движения тела 4
2.1. Основные определения и формулы
2.2. Равноускоренное движение тела. Движение в поле тяжести Земли
2.3. Влияние воздушной атмосферы на движение тела
3. Расчетно-теоретические исследования особенностей движения тела, брошенного под углом к горизонту, в поле тяжести Земли
3.1. Траектория движения тела в однородном поле тяжести
3.2. Траектория движения тела в однородном поле тяжести с учетом влияния воздушной атмосферы
4. Экспериментальное исследование движения тела в поле тяжести Земли
4.1. Состав, назначение и характеристики экспериментальной установки
4.2. Результаты экспериментов. Пересчет начальной скорости полета снаряда
5. Применение теоретических основ механики движения тела в однородном поле тяжести для игры "Angry birds"
5.1. Описание игры "Angry birds"
5.2. Определение траектории полета птиц и сопоставление их масс
6. Заключение
1. Введение
Данная работа посвящена исследованию механики (кинематики и динамики) движения тела. Цель работы: изучить движение тела в однородном поле тяжести, используя расчетно-теоретический и экспериментальный подходы.
Задачи, которые необходимо решить для достижения поставленной цели:
1) Вывести основные соотношения для движения тела в однородном поле тяжести; описать влияние воздушной атмосферы на полет тела.
2) Получить траекторию движения тела в однородном поле тяжести; учесть влияние воздушной атмосферы и рассчитать траекторию движения с помощью метода Ньютона.
3) Создать экспериментальную установку, с помощью которой можно запускать снаряд (шар) с заданной скоростью под заданным углом к горизонту.
4) Измерить дальность полета шара в эксперименте и провести интерпретацию полученных экспериментальных данных.
5) Исследовать траектории полета птиц в игре «Angry birds», применить к ним имеющиеся соотношения из механики движения тела.
2. Теоретические основы механики движения тела
2.1. Основные определения и формулы
Механика - раздел физики, изучающий движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени положения тел или их частей в пространстве [1]. Все исследования, проводимые в данной работе, находятся в рамках классической механики, т. е. рассматриваются макрообъекты, движущиеся со скоростями гораздо меньшими, чем скорость света.
Для описания движения тел, если это дополнительно не оговорено, будет использоваться модель материальной точки. Материальная точка - это идеальное тело, размеры которого считаются бесконечно малыми по сравнению с другими размерами в рассматриваемой задаче. Положение материальной точки в пространстве определяется как положение геометрической точки.
Чтобы описывать движение тела необходимо ввести понятие системы отсчета. Система отсчета - это совокупность системы координат и "привязанным" к данной системе координат часам. Обычно для описания пространственного положения тела используется декартова прямоугольная система координат, где координатные оси перпендикулярны друг другу.
Пусть тело из точки А переместилось в точку В (см. рис. 1). Тогда перемещением тела ![]() называется вектор
называется вектор ![]() . Траекторией материальной точки называется линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своем перемещении в пространстве. Таким образом, траекторией движения тела на рис. 1 является кривая АВ. Положение материальной точки в каждый момент времени определяется радиус-вектором
. Траекторией материальной точки называется линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своем перемещении в пространстве. Таким образом, траекторией движения тела на рис. 1 является кривая АВ. Положение материальной точки в каждый момент времени определяется радиус-вектором ![]() , начало которого совпадает с началом координат, а конец - с положением материальной точки.
, начало которого совпадает с началом координат, а конец - с положением материальной точки.
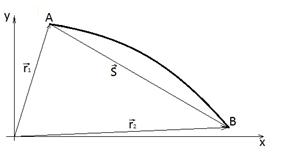
Рис. 1. Траектория движения и перемещение тела
Скорость - векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчета:
![]() , (1)
, (1)
где t - время, за которое тело переместилось из точки А в точку В (см. рис. 1). Строго говоря, формульное определение, данное выше, соответствует средней скорости на всем участке АВ. Однако очевидно, что скорость на протяжении относительно длинного участка пути может изменяться. Чтобы определить, как изменяется скорость при движении тела, нужно разбить весь путь на небольшие участки и найти среднюю скорость на этих участках. Чем меньше участки, тем точнее можно получить зависимость скорости от времени, прошедшего с начала движения, или от текущего положения тела.
Аналогично скорости вводится ускорение тела. Ускорением называется векторная величина, характеризующая темп изменения скорости тела:
![]() , (2)
, (2)
где ![]() - скорости тела в начальный и конечный момент времени движения, t - время движения. Для получения подробной зависимости ускорения от времени необходимо также дробить весь пройденный телом путь на короткие участки и находить среднее ускорение по формуле (2) на этих участках.
- скорости тела в начальный и конечный момент времени движения, t - время движения. Для получения подробной зависимости ускорения от времени необходимо также дробить весь пройденный телом путь на короткие участки и находить среднее ускорение по формуле (2) на этих участках.
2.2. Равноускоренное движение тела. Движение тела в поле тяжести Земли.
Частным случаем движения тела является равноускоренное движение, при котором ускорение тела все время имеет одну и ту же величину и направление.
Выберем направление координатной оси x так, чтобы оно совпадало с направлением вектора ускорения. Пусть также скорость в начальный момент времени t=0 с совпадает по направлению с ускорением и равняется 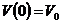 , а положение тела в начальный момент времени соответствует координате
, а положение тела в начальный момент времени соответствует координате 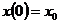 . Тогда, по формуле (2), можно получить, что в некоторый момент времени t скорость будет равна:
. Тогда, по формуле (2), можно получить, что в некоторый момент времени t скорость будет равна:
![]() . (3)
. (3)
Поскольку скорость нарастает линейно, то для определения координаты тела в момент времени t можно использовать значение средней скорости за этот промежуток времени: 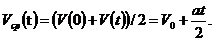
Таким образом, можно получить теперь по формуле (1), что:
![]() (4)
(4)
Формулы (3) и (4) являются основными для описания параметров тела в случае равноускоренного движения.
Движение тела у поверхности Земли (в практически однородном поле тяжести) является равноускоренным, поскольку ускорение, которое испытывает тело, представляет из себя ускорение свободного падения ![]() , направленное вертикально вниз и равное по величине 9,8 м/с2.
, направленное вертикально вниз и равное по величине 9,8 м/с2.
Направим ось Ox горизонтально, а ось Oy - вертикально вверх (см. рис. 2). В этом случае проекции ускорения на координатные оси выглядят следующим образом: 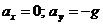 . Применим далее формулы (2) и (3) для определения зависимостей компонент скорости от времени:
. Применим далее формулы (2) и (3) для определения зависимостей компонент скорости от времени:
![]() , (5)
, (5)
где ![]() - компоненты начальной скорости движения тела,
- компоненты начальной скорости движения тела, ![]() - угол вектора начальной скорости к горизонту.
- угол вектора начальной скорости к горизонту.
Чтобы найти зависимость координат точки от времени необходимо применить формулы (2) и (4). Таким образом, получаем:
![]() , (6)
, (6)
где ![]() - координаты тела в момент времени t=0c.
- координаты тела в момент времени t=0c.
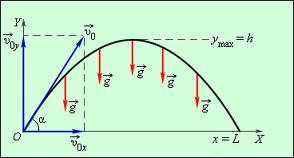
Рис. 2. К выводу формул (5) и (6).
2.3. Влияние воздушной атмосферы на движение тела
Соображения, приведенные в п. 2.2, и, соответственно, формулы, полученные там же, верны в следующих приближениях: 1) поверхность земли является горизонтальной (т. е. расстояния достаточно малы и можно было пренебречь сферичностью поверхности); 2) поле тяжести однородно; 3) отсутствует атмосфера (или любая другая окружающая среда). Первые два приближения достаточно неплохо выполняются на небольших расстояниях. Влияние окружающей воздушной атмосферы на полет тела необходимо исследовать дополнительно, что и будет проделано ниже.
Прежде всего необходимо понять, какое движение возникает в воздухе во время полета в нем какого-нибудь тела. Здесь следует упомянуть так называемый принцип взаимности, который следует из преобразований Галилея: для определения аэродинамической силы, действующей на тело, можно рассматривать как движение тела в изначально покоящемся газе, так и обтекание неподвижного тела газом, движущимся со скоростью, равной скорости тела. В дальнейшем в зависимости от того, что более удобно, будут использоваться оба подхода.
Изучим для примера поперечное обтекание длинного круглого цилиндра [2, 3]. Если скорость натекающего газа мала, то картина обтекания практически симметрична (см. рис. 3а). Можно показать, что в таком случае сила сопротивления, действующая на цилиндр со стороны газа, равна нулю. Данный факт называется парадоксом Даламбера.
Тем не менее, согласно многочисленным экспериментальным данным, практически всегда сила сопротивления движению тела не равна нулю. Это связано с тем, что при увеличении скорости натекающего газа картина течения существенным образом меняется (см. рис. 3б). С подветренной стороны цилиндра образуются два вихря, при этом давление с подветренной стороны становится ниже, чем с наветренной. Образующийся перепад давлений порождает силу, которая и является силой аэродинамического сопротивления.
Следует сказать, что при дальнейшем увеличении скорости натекания газа картина течения продолжает эволюционировать. Два вихря, расположенные у подветренной поверхности цилиндра, начинают по очереди "отрываться" и двигаться вместе с потоком газа. Образуется так называемая "дорожка Кармана" (см. рис. 3в).
а) б)
б)
в)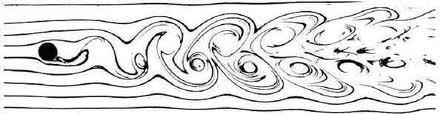
Рис. 3. Картины поперечного обтекания длинного круглого цилиндра потоком газа различной скорости.
Картину течения характеризует число Рейнольдса: ![]() , где
, где ![]() - плотность газа,
- плотность газа, ![]() - скорость газа относительно тела,
- скорость газа относительно тела, ![]() - диаметр цилиндра (в общем случае, характерный размер тела),
- диаметр цилиндра (в общем случае, характерный размер тела), ![]() - динамическая вязкость газа. Согласно исследованиям, при
- динамическая вязкость газа. Согласно исследованиям, при ![]() образуются вихри и, следовательно, возникает аэродинамическая сила сопротивления.
образуются вихри и, следовательно, возникает аэродинамическая сила сопротивления.
В эксперименте, проводимом в работе (см. п. 4.2), изучается движение шара в воздушной атмосфере. Картина обтекания шара отличается от картины обтекания цилиндра. Изобразить ее на плоскости достаточно сложно, поскольку она существенно трехмерная. Тем не менее, основные зависимости для силы сопротивления сохраняются. Силу сопротивления можно определить по формуле:
![]() , (7)
, (7)
где ![]() - площадь Миделя,
- площадь Миделя, ![]() - коэффициент, который определяется картиной течения. Зависимость коэффициента
- коэффициент, который определяется картиной течения. Зависимость коэффициента ![]() от числа Рейнольдса
от числа Рейнольдса ![]() изображена на рис. 4.
изображена на рис. 4.
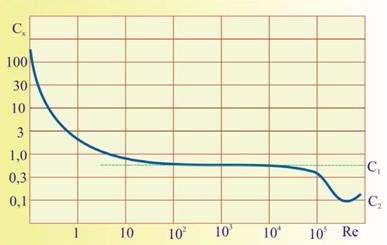
Рис. 4. Зависимость коэффициента С от числа Рейнольдса ![]()
2.4. Расчетный метод Ньютона.
Во многих случаях оказывается невозможным получить конечное аналитическое решение поставленной задачи. В подобных случаях единственный выход – искать численное решение исходных уравнений, применяя тот или иной численный метод. Ниже будет рассказано о расчетном методе Ньютона.
Полное описание расчетного метода Ньютона с необходимыми доказательствами в данном пункте нецелесообразно, поскольку он используется исключительно для расчета траектории полета шара в однородном поле тяжести в воздушной атмосфере. Проиллюстрируем применение метода Ньютона в данном конкретном случае.
Предположим, что в начальный момент времени t=0 с положение шара и его скорость известны: ![]() . Сила, действующая на шар, складывается из силы тяжести, направленной вертикально вниз, и аэродинамической силы сопротивления, направленной противоположно скорости движения шара (см. рис. 5):
. Сила, действующая на шар, складывается из силы тяжести, направленной вертикально вниз, и аэродинамической силы сопротивления, направленной противоположно скорости движения шара (см. рис. 5): 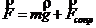 , где
, где ![]() - масса шара.
- масса шара.
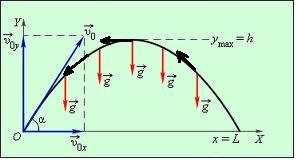
Рис. 5. Силы, действующие на тело в полете.
Найдем ускорение шара из второго закона Ньютона: 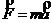 . Таким образом,
. Таким образом,
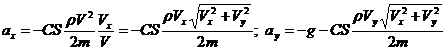 . (8)
. (8)
Площадь Миделя шара ![]() , где
, где ![]() - радиус шара.
- радиус шара.
Принцип, заложенный в расчетном методе Ньютона, заключается в том, что за очень малый промежуток времени параметры полета меняются слабо, поэтому можно пренебречь изменением некоторых из них. Сразу следует оговориться, что данные метод приближенный, т. е. выдает неточные результаты. Тем не менее, появляется возможность провести расчеты на компьютере и выбрать шаг по времени настолько малый, чтобы была достигнута необходимая точность вычислений.
Итак, зная параметры полета шара в начальный момент времени, нужно рассчитать те же самые параметры в следующий момент времени, когда прошел малый промежуток времени ![]() . Обозначим параметры в следующий момент времени индексом «1». Согласно принципу, заложенному в методе Ньютона, полагаем, что за
. Обозначим параметры в следующий момент времени индексом «1». Согласно принципу, заложенному в методе Ньютона, полагаем, что за ![]() ускорение не успевает измениться, поэтому вычисляем значения проекций ускорения на координатные оси по формулам (8), при этом проекции скоростей берутся в начальный момент времени. Считая ускорение постоянным, определяем, как изменилась скорость, а затем и перемещение тела по формулам (5) и (6). Окончательно получаем следующую цепочку вычислений:
ускорение не успевает измениться, поэтому вычисляем значения проекций ускорения на координатные оси по формулам (8), при этом проекции скоростей берутся в начальный момент времени. Считая ускорение постоянным, определяем, как изменилась скорость, а затем и перемещение тела по формулам (5) и (6). Окончательно получаем следующую цепочку вычислений:
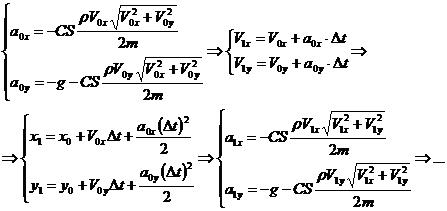 (9)
(9)
Проводя вычисления по данной цепочке далее, можно определить траекторию движения шара, при этом чем меньше величина ![]() , тем ближе расчетная траектория к истинной.
, тем ближе расчетная траектория к истинной.
3. Расчетно-теоретические исследования особенностей движения тела, брошенного под углом к горизонту, в поле тяжести Земли
3.1. Траектория движения тела в однородном поле тяжести
Воспользуемся формулами (6) для определения траектории движения материальной точки в однородном поле тяжести в отсутствии окружающей атмосферы. Выразим t из первого уравнения (6) и подставим полученное выражение во второе уравнение:
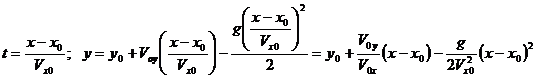 . (10)
. (10)
Как видно из второго уравнения (10), траектория движения представляет собой параболу. Несколько траекторий, рассчитанных для различных начальных условий, приведены на рис. 6.
а) 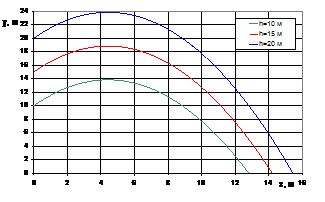
б)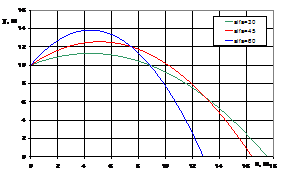 в)
в)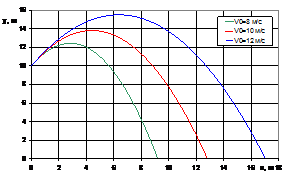
Рис. 6. Траектории движения материальной точки в однородном поле тяжести: а) ![]() =10 м/с,
=10 м/с, ![]() =60°, начальная высота h меняется; б) h=10 м,
=60°, начальная высота h меняется; б) h=10 м, ![]() =10 м/с, угол
=10 м/с, угол ![]() меняется; в) h=10 м,
меняется; в) h=10 м, ![]() =60°, начальная скорость
=60°, начальная скорость ![]() меняется.
меняется.
3.2. Траектория движения тела в однородном поле тяжести с учетом влияния воздушной атмосферы
Для определения искомой траектории движения шара с учетом влияния воздушной атмосферы необходимо провести вычисления по цепочке (9).
В качестве предварительной проверочной работы были проведены расчеты по методу Ньютона без учета влияния воздуха. Логично ожидать в этом случае, что расчетные траектории будут совпадать с истинной, поскольку в целом движение равноускоренное, поэтому дробление всего пути на малые участки и применение к ним формул для равноускоренного движения равносильно применению этих же формул для всего полета. Результаты расчетов представлены на рис. 7.
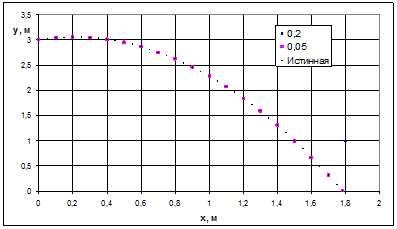
Рис. 7. Траектория движения шара в однородном поле тяжести (аналитическая и расчетные кривые совпадают).
Далее проводится расчет траектории движения шара уже с учетом влияния атмосферы. Однако для проведения данных вычислений не достаточно данных, поскольку коэффициент С не известен.
Особый интерес вызывает определение траектории движения для случая, реализуемого в эксперименте (см. п. 4.2). По оценкам, полученным на основе экспериментальных данных, скорость шара составляет около 4 м/с. Определим число Рейнольдса для данного случая: ![]() . Обращаясь к графику на рис. 4, видим, что в данном диапазоне, коэффициент С практически не меняется. Можно принять, что С=0,6. Результаты расчета траектории движения шара с учетом влияния атмосферы приведены на графике (рис. 8).
. Обращаясь к графику на рис. 4, видим, что в данном диапазоне, коэффициент С практически не меняется. Можно принять, что С=0,6. Результаты расчета траектории движения шара с учетом влияния атмосферы приведены на графике (рис. 8).
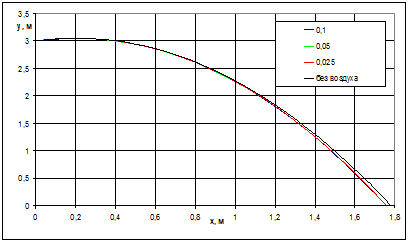
Рис. 8. Расчетные траектории движения шара с учетом и без учета влияния атмосферы для разных шагов по времени.
Относительная разница между величинами дальности полета, рассчитанными для различных шагов по времени. не превышает 0,06%. Из графика видно, что наличие атмосферы, безусловно, влияет на траекторию движения шара, однако на расстояниях, характерных для эксперимента, это влияние достаточно мало (около 1%), и, следовательно, им можно пренебречь.
4. Экспериментальное исследование движения тела в поле тяжести Земли
4.1. Состав, назначение и характеристики экспериментальной установки
Основным назначением экспериментальной установки является придание некоторому телу заданной начальной скорости, а также угла наклона начальной скорости к горизонту. В качестве простейшего прообраза экспериментальной установки выступает обычная рогатка.
После предварительной проработки проекта была создана следующая установка (см. рис. 9). В края доски 1 с плоской (по уровню) поверхностью вкручены два самореза 2, к которым прикреплена полоска резины 3. В низу доски 1 расположен спусковой механизм 4, который «взводится» и позволяет выстреливать по нажатию на него. В качестве снаряда выбран пластиковый полнотелый шар 5, диаметром 4 см и массой около 30 г. Для более надежного фиксирования шара перед выстрелом на резиновую полоску одета более широкая кожаная полоска 6. Поскольку растяжение резиновой полоски осуществляется на одну и ту же величину, то предполагается, что шар будет ускоряться до одной и той же скорости. С обратной стороны доска 1 крепится к подставке 7 с помощью шарниров 8, которые позволяют устанавливать поверхность доски под разными углами к горизонту. При этом нижняя часть доски всегда опирается на землю.


Рис. 9. Схема экспериментальной установки: 1 – доска; 2 – саморезы; 3 – резиновая полоска; 4 – спусковой механизм; 5 – снаряд (шар); 5 – кожаная полоска; 6 – подставка; 7 – шарниры.
4.2. Результаты экспериментов. Пересчет начальной скорости полета снаряда
Все измерения в эксперименте производились с помощью измерительной рулетки или линейки. Измерялись следующие величины (см. рис. 10): 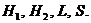
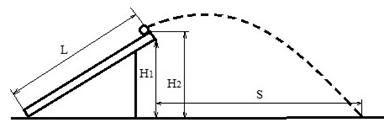
Рис. 10. Схема проведения эксперимента.
В основном, эксперименты проводились на ровной поверхности, однако при наличии небольших неровностей они учитывались. Было проведено две серии экспериментов. Каждая серия состояла из экспериментов, проводимых для разных углов наклона доски к горизонту. В рамках одного положения по отношению к горизонту запуски повторялись несколько (от трех до пяти) раз. Результаты экспериментов приведены в таблице 1.
Таблица 1. Результаты экспериментальных данных (в см).
№ эксп | H1 | S1 | S2 | S3 | S4 | S5 | Sсредн | H2 |
1 | 6,1 | 74 | 84 | 75 | 79 | 78 | 78 | 7,7 |
2 | 8,5 | 87 | 100 | 93 | 91 | 91 | 92,4 | 10,5 |
3 | 13,5 | 119 | 122 | 115 | 120 | 120 | 119,2 | 15 |
4 | 18 | 108 | 116 | 119 | 121 | 121 | 117 | 19,5 |
5 | 23,5 | 121 | 153 | 140 | 139 | 139 | 138,4 | 25 |
1 | 6,1 | 80 | 80 | 80 | 80 | 7,8 | ||
2 | 9,4 | 107 | 107 | 108 | 108 | 107,5 | 11 | |
3 | 13,5 | 130 | 130 | 130 | 15 | |||
4 | 19,9 | 173 | 175 | 177 | 175 | 21,2 | ||
5 | 24,9 | 200 | 202 | 205 | 204 | 202,75 | 26,2 |
Для интерпретации полученных экспериментальных данных было решено решить обратную задачу, т. е. по дальности полета шара определить его начальную скорость. Итак, известны координаты начала движения тела ![]() , а также угол наклона начальной скорости к горизонту
, а также угол наклона начальной скорости к горизонту ![]() , а также дальность полета S. Кроме того, судя по результатам расчетов, приведенных в п. 3.2, влиянием атмосферы можно пренебречь. Следовательно, используем формулы (6), помня при этом, что
, а также дальность полета S. Кроме того, судя по результатам расчетов, приведенных в п. 3.2, влиянием атмосферы можно пренебречь. Следовательно, используем формулы (6), помня при этом, что 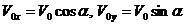 . Тогда получаем, что
. Тогда получаем, что ![]() Выразим t из первого уравнения и подставим во второе:
Выразим t из первого уравнения и подставим во второе:
![]() .
.
Когда шар упадет, его ордината у станет равна нулю, а абсцисса – дальности полета S. Зная этот факт, найдем ![]() :
:
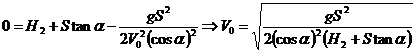 . (11)
. (11)
Результаты пересчета начальной скорости по дальности полета приведены на графике (рис. 11). Глядя на график, можно сделать вывод, что начальная скорость, приобретаемая шаром, составляет примерно 4 м/с. Также при значении величины угла ![]() большем, чем 20°, появляется сильный разброс начальных скоростей, который объясняется тем, что снаряд в пусковом устройстве каждый раз размещается несколько по-разному.
большем, чем 20°, появляется сильный разброс начальных скоростей, который объясняется тем, что снаряд в пусковом устройстве каждый раз размещается несколько по-разному.
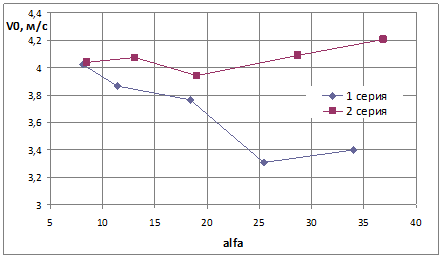
Рис. 11. Зависимость начальной скорости шара от угла наклона плоскости к горизонту.
5. Применение теоретических основ механики движения тела в однородном поле тяжести для игры "Angry birds"
5.1. Описание игры "Angry birds"
Предыстория сюжета игры проста [4]: свиньи украли яйца из гнезд птиц, птицы, соответственно, отправляются мстить за нанесенный урон. Однако месть их реализуется весьма экстравагантным методом. В то время, как свиньи прячутся за деревянными, стеклянными или каменными (в зависимости от уровня) конструкциями, птицы «заряжаются» в рогатку, выстреливаются и летят к свиньям, прошибая, по всей видимости, весьма прочной головой все препятствия. Цель: поразить всех свиней. Количество доступных птиц в каждом уровне ограничено. Начальной скоростью и углом наклона вектора начальной скорости к горизонту управляет в ручном режиме игрок.
С точки зрения проводимых исследований весьма интересно изучить траекторию полета птицы и узнать, соответствует ли она траектории полета тела в однородном поле тяжести.
5.2. Определение траектории полета птиц и сопоставление их масс
Функционал игры позволяет нам работать с траекториями полета птиц. После пролета очередной птицы и до выстрела следующей на экране точечной линией отображается траектория полета. Сделав скриншот такого экрана, можно изучить траекторию полета. Нужно выбрать системы координат и определить абсциссы и ординаты точек траектории в каких-нибудь условных единицах, например, в пикселях (см. рис. 12).

Рис. 12. Измерение параметров траектории полета птицы (белые точки – траектория).
Траектории полета для различных типов птиц приведены на рис. 13. В основном, все птицы летят по одной траектории, и только птица, названная нами в рабочем порядке «большой», имеет более низкую траекторию и, следовательно, ее начальная скорость ниже, чем у остальных.
Через точки траектории была проведена наилучшая кривая из класса кривых второго порядка. Как видно, коэффициент детерминации (![]() ) близок к 1. Таким образом, можно утверждать, что траектория полета представляет собой параболу, а полет птиц соответствует движению в поле однородном поле тяжести. Это означает, что траектория должна описываться формулами (10). Функционал программы MSExcel позволяет получить уравнение наилучшей кривой, коэффициенты которого можно соотнести с параметрами из уравнения (10).
) близок к 1. Таким образом, можно утверждать, что траектория полета представляет собой параболу, а полет птиц соответствует движению в поле однородном поле тяжести. Это означает, что траектория должна описываться формулами (10). Функционал программы MSExcel позволяет получить уравнение наилучшей кривой, коэффициенты которого можно соотнести с параметрами из уравнения (10).
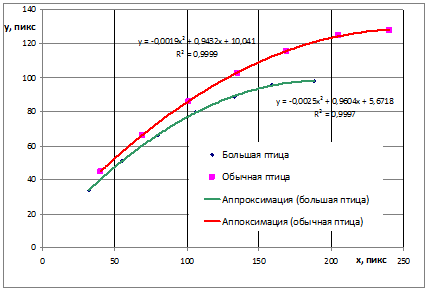
Рис. 13. Траектории полета для различных типов птиц.
Как видно из уравнения траектории (10), свободный член может возникнуть только, если ![]() или
или ![]() не равны нулю. При измерениях система координат выбиралась таким образом, чтобы начало координат совпадало с местом начала полета. Тем не менее, птица – это достаточно крупный объект, поэтому погрешность в определении центра данного объекта привела к появлению свободного члена в уравнении траектории.
не равны нулю. При измерениях система координат выбиралась таким образом, чтобы начало координат совпадало с местом начала полета. Тем не менее, птица – это достаточно крупный объект, поэтому погрешность в определении центра данного объекта привела к появлению свободного члена в уравнении траектории.
Коэффициент при x равняется ![]() . Таким образом, можно получить, что угол к горизонту, под которым бросили большую птицу,
. Таким образом, можно получить, что угол к горизонту, под которым бросили большую птицу, ![]() =43,8°, малую птицу
=43,8°, малую птицу ![]() =43,3°.
=43,3°.
Коэффициент при ![]() , согласно уравнению (10), равен
, согласно уравнению (10), равен ![]() . Используя данные из графика (рис. 13) и величины углов, полученные выше, получаем:
. Используя данные из графика (рис. 13) и величины углов, полученные выше, получаем: ![]() . Конечно, никак нельзя узнать, чему равно g, особенно в принятых нами условных единицах. Тем не менее, один интересный вывод сделать все-таки можно. Предположим, что резина рогатки передает птицам одинаковую энергию. Эта энергия переходит в кинетическую энергию птицы
. Конечно, никак нельзя узнать, чему равно g, особенно в принятых нами условных единицах. Тем не менее, один интересный вывод сделать все-таки можно. Предположим, что резина рогатки передает птицам одинаковую энергию. Эта энергия переходит в кинетическую энергию птицы ![]() . Значит, отношение масс птиц
. Значит, отношение масс птиц ![]() , т. е. большая птица на 30% тяжелее.
, т. е. большая птица на 30% тяжелее.
6. Заключение
В работе осуществлен комплексный (расчетно-теоретический и экспериментальный) подход к изучению движения тела в однородном поле тяжести. По результатам работы можно сделать следующие выводы.
1) Траектория движения материальной точки в однородном поле тяжести является параболой.
2) Погрешность расчета дальности полета тела по методу Ньютона при использовании шага по времени ![]() =0,025с не превышает 0,06%.
=0,025с не превышает 0,06%.
3) При малых расстояниях полета (до 3 м) влияние окружающей атмосферы на траекторию полета шара пренебрежимо мало (около 1%).
4) Создана экспериментальная установка, способная бросать снаряд (шар) с одной и той же начальной скоростью при разных углах наклона вектора начальной скорости к горизонту (стабильно работает при углах до 20°).
5) Птицы в игре «Angry birds» двигаются, как тела в однородном поле тяжести, следовательно, к их полету можно применять соотношения из механики.
6) Показано, что, анализируя траекторию полета птицы, можно найти угол, под которым она была брошена; определено, что большая птица на 30% тяжелее, чем все остальные.
Список литературы
1. Пинский физики: В 2 т: Т. 1: Механика; Молекулярная физика; Электродинамика. 4-е переработанное издание. М.: 2001.
2. , Вознесенский в механику жидкости и газа: [учеб. пособие]. М.: МФТИ, 2007.
3. Абрамович газовая динамика. Учеб. руководство: Для втузов. 5-е изд., перераб. и доп. - М.: Наука. Гл. ред. физ-мат. лит, 1991.
4. http://chrome. /.



