Сетевой график.

Справочный материал.

1. Составляющие сетевого графика.

Событие - геометрическая фигура, например, круг с шифром внутри.

Работа (с затратой времени) – стрелка или направленная дуга.

Фиктивная работа ( без затрат времени) – пунктирная стрелка.

Замечание. При построении сетевого графика желательно соблюдать направление стрелок слева-направо.

2. Основные понятия сетевого графика.

Исходное событие(исток)- первоначальное событие(обозначается I).

Завершающее событие(сток) - конечное событие (обозначается С).

Шифр работы- (i, j), где i – шифр события начала работы, j– шифр события окончания работы.

Путь – последовательность работ, в которой конечное событие одной работы совпадает с начальным событием следующей (обозначается (i, j)- путь между событиями i и j).

Продолжительность работы - tij

Длина пути – сумма продолжительностей работ пути.

Предшествующее событие – событие, располагающееся перед данным событием так, что между ними нет никаких событий.

Последующее событие – событие, располагающееся после данного события так, что между ними нет никаких событий.

Полный путь – путь от истока к стоку.

Путь, предшествующий событию s – путь (I, s).

Путь, последующий за событием s – путь (s, C).

Характерные ошибки.

Работа не должна иметь одинаковых шифров, т. е. два события не должны быть соединены более, чем одной стрелкой. В сети должно быть только одно тупиковое событие – сток (обозначается C). В сети должно быть только одно начальное событие – исток (обозначается I). В сети не должно быть циклов.

Свойства сетевых графиков.

Ни одно событие не может произойти ранее окончания всех входящих в него работ. Ни одна работа, выходящая из данного события, не может произойти ранее данного события.

3. Правильная нумерация.

Правильная нумерация – это нумерация событий, при которой любой путь идет через события с возрастающими номерами.

Алгоритм вычеркивания дуг.

Шаг 0. Истоку присваивается ранг 0.

Вычеркиваем все работы, выходящие из события 0.

Шаг k. Всем оставшимся событиям без входящих дуг присваиваем ранг k.

Вычеркиваем все работы, выходящие из событий k.

Нумеруем эти работы последовательными числами натурального ряда, начиная с наименьшего еще не использованного числа в предыдущем шаге алгоритма.

Замечание. Максимальное число дуг предшествующих путей события k – того ранга равно k.

4.Параметры сетевого графика.

Критический путь – путь максимальной длины от истока к стоку.

А) Сроки событий и работ.

Наиболее раннее из возможных сроков свершения события назовем срок, необходимый для выполнения всех работ, предшествующих данному событию, т. е. длина максимального пути из всех путей, предшествующих событию .

,

Наиболее поздний из допустимых сроков назовем такой срок свершения события , превышение которого вызовет аналогичную задержку наступления завершающего события.

,

,

.

Самый ранний срок начала работы

.

Самый ранний срок окончания работы

.

Самый поздний срок начала работы

.

Самый поздний срок окончания работы

.

Б) Резервы времени.

Резерв времени события 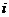- это промежуток времени, на который может быть отсрочено свершение этого события.

.

Замечание. Путь, соединяющий события с нулевым резервом времени, является критическим путем.

Полный резерв времени работы – это максимальное количество времени, на которое можно увеличить продолжительность работы , не изменяя продолжительность критического пути.

.

Свободный резерв времени работы - это максимальное количество времени, на которое можно увеличить продолжительность работы или отсрочить ее начало, не изменяя ранних сроков начала последующих работ.

Руководство к выполнению лабораторной работы (табличный метод).

Графа 2 (код работы) заполняется на основе сетевого графика или перечня работ, расположенных в порядке их выполнения. Графа 1 (количество предшествующих работ). Для работ оно равно 0. Для остальных работ оно определяется по числу работ с кодом. Графа 3 (продолжительность работ) заполняется согласно заданию. Графы 4 и 5 (раннее начало и раннее окончание работ) заполняются одновременно. . . Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ . Раннее окончание работы находится как сумма раннего начала и продолжительности работы , т. е. .

Продолжительность критического пути равна 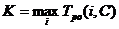( графа 5).

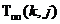Графа 7 (позднее окончание работ). Величину К заносим в графу 7 для всех . Заполняем снизу вверх. Позднее окончание работы определяется как минимум разностей позднего окончания и продолжительностью работы для всех последующих работ . Графа 6 (позднее начало работ) находится как разность позднего окончания этих работ и их продолжительности (из значения графы 7 вычитаем значение графы 3). Графа 8 (полный резерв времени работы) определяется разностью между значениями графы 7 и 5 (или 6 и 4). Графа 10 (резерв времени события). , где

( из графы 7), (из графы 4).

9. Графа 9 (свободный резерв времени) определяется вычитанием значений графы 10 из значений графы 8.

Лабораторная работа.

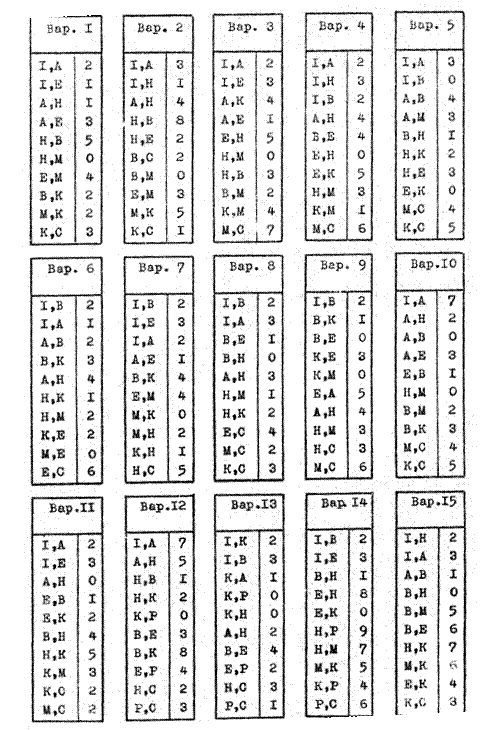
Дано. Коды работ, их продолжительность (таблица в соответствии с номером варианта).

Требуется.

Построить сетевой график. Выполнить правильную нумерацию событий. Рассчитать параметры сетевого графика табличным методом. Определить критический путь.