Ãîñóäàðñòâåííûé êîìèòåò Ðîññèéñêîé ôåäåðàöèè ïî âûñøåìó îáðàçîâàíèþ
ÓÐÀËÜÑÊÈÉ ÃÎÑÓÄÀÐÑÒÂÅÍÍÛÉ ÒÅÕÍÈ×ÅÑÊÈÉ ÓÍÈÂÅÐÑÈÒÅÒ![]() - ÓÏÈ
- ÓÏÈ
Т
Теплофизика
Ìåòîäè÷åñêèå óêàçàíèÿ ê ëàáîðàòîðíûì ðàáîòàì ¹ 1,3,5 äëÿ ñòóäåíòîâ ôèçèêî-òåõíè÷åñêîãî ôàêóëüòåòà
Åêàòåðèíáóðã
Лабораторная работа №1
ВВЕДЕНИЕ
Процессы теплообмена при изменении агрегатного состояния вещества составляют основу технологических процессов в теплоэнергетике, химической технологии, криогенной технике и раде других отраслей современной техники. Кризис теплоотдачи при кипении (кризис кипения) является частным случаем теплообмена при изменении агрегатного состояния вещества и имеет важнейшее значение в условиях охлаждения высокотемпературных, форсированных теплоотдающих поверхностей. В настоящей лабораторной работе изучается кризис кипения при температуре насыщения двуокиси углерода на погруженной тонкой горизонтальной цилиндрической поверхности.
1. ЯВЛЕНИЕ КРИЗИСА ТЕПЛООТДАЧИ ПРИ КИПЕНИИ
1.1. Два режима кипения
Известны два режима кипения. В зависимости от плотности теплового потока, подводимого к жидкости через греющую поверхность. на последней возникают отдельные паровые пузыри или образуется сплошной слой пара. Первый процесс называют пузырьковым кипением, второй - пленочным кипением. При пузырьковом кипении жидкость омывает поверхность нагрева, ее пограничный слой интенсивно турбулизуется возникающими пузырьками. Всплывающими пузырями осуществляется также скрытый теплоперенос, вызываемый испарением на нижней стенке и конденсацией на вершине пузыря. Создается интенсивный молярный перенос теплоты от поверхности нагрева к массе кипящей жидкости. Следствием этого является высокая интенсивность теплоотдачи при пузырьковом кипении.
При пленочном кипении жидкость отделена от поверхности сплошной пленной пара, с внешней стороны которой отрываются и всплывают паровые образования. Вследствие низкой теплопроводности пара интенсивность теплоотдачи в условиях пленочного кипения существенно меньше, чем при пузырьковом.
С возрастанием температуры поверхности TW (или температурного напора 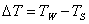 , где TW температура насыщения) плотность теплового потока q а также коэффициент теплоотдачи a при пузырьковом кипении увеличивается. Однако рост этот не беспределен. Рассмотрим экспериментально полученные зависимости
, где TW температура насыщения) плотность теплового потока q а также коэффициент теплоотдачи a при пузырьковом кипении увеличивается. Однако рост этот не беспределен. Рассмотрим экспериментально полученные зависимости ![]() и
и ![]() для воды при ее кипении на горизонтальной поверхности, обогреваемой паром, при атмосферном давлении (рис. 1.1).
для воды при ее кипении на горизонтальной поверхности, обогреваемой паром, при атмосферном давлении (рис. 1.1).
Остановимся на зависимости 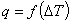 . Можно выделить несколько областей кривой. АВ - интенсивность теплообмена с малыми температурными напорами, определяется в основном условиями гравитационного свободного движения. Число центров парообразования невелико, и пузыри слабо турбулизуют пристеночный слой. ВС - область начала и развитого пузырькового кипения, характеризуется интенсивным ростом величин q и a.. CD переходная область.
. Можно выделить несколько областей кривой. АВ - интенсивность теплообмена с малыми температурными напорами, определяется в основном условиями гравитационного свободного движения. Число центров парообразования невелико, и пузыри слабо турбулизуют пристеночный слой. ВС - область начала и развитого пузырькового кипения, характеризуется интенсивным ростом величин q и a.. CD переходная область.
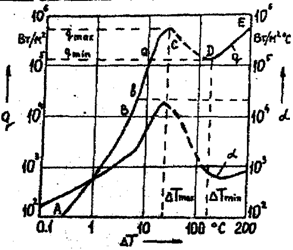
Рис. 1.1. Характер зависимостей ![]() и
и ![]() при кипении воды в большом объеме под атмосферным давлением
при кипении воды в большом объеме под атмосферным давлением
При некотором температурном напоре ![]() , зависящем от рода жидкости, состояния и характера поверхности, давления (точка С), паровые пузыри на части поверхности образуют сплошную пленку пара, препятствующую контакту жидкости с поверхностью. Пузырьковый режим кипения сменяется пленочным. В результате происходит резкое снижение плотности теплового потока q и коэффициента a.
, зависящем от рода жидкости, состояния и характера поверхности, давления (точка С), паровые пузыри на части поверхности образуют сплошную пленку пара, препятствующую контакту жидкости с поверхностью. Пузырьковый режим кипения сменяется пленочным. В результате происходит резкое снижение плотности теплового потока q и коэффициента a.
Это явление перехода от пузырькового режима кипения к пленочному носит название кризиса теплоотдачи при кипении.
1.2. Кризис теплоотдачи при кипении
Кризис теплоотдачи при кипении изменение механизма (закономерностей) теплоотдачи в начале перехода от пузырькового кипения к пленочному или от пленочного кипения к пузырьковому. Переход от пузырькового кипения к пленочному сопровождается ухудшением теплоотдачи; при кипении газо - (паро-) жидкостной смеси к такому эффекту может приводить и высыхание пленки жидкости на обогреваемой поверхности. Из сказанного становится ясно, что существуют кризисы кипения различного рода, и это подтверждается экспериментальными данными последнего времени.
Максимально возможная (при данных условиях) плотность теплового потока при пузырьковом кипении называется первой критической плотностью теплового потока ![]() . При плотностях теплового потока, больших первой критической, чистая форма пузырькового кипения невозможна. Температурный напор и температуру обозначим соответственно
. При плотностях теплового потока, больших первой критической, чистая форма пузырькового кипения невозможна. Температурный напор и температуру обозначим соответственно ![]() и
и![]() . Температурные напоры, отвечающие
. Температурные напоры, отвечающие ![]() и
и ![]() , неодинаковы: максимум коэффициента теплоотдачи несколько сдвинут относительно
, неодинаковы: максимум коэффициента теплоотдачи несколько сдвинут относительно ![]() в сторону меньших температурных напоров (рис. 1.1).
в сторону меньших температурных напоров (рис. 1.1).
Наибольшее признание и последующее развитие получила гидродинамическая теория кризиса кипения, разработанная для кипения в большом объеме. Эта теория с успехом используется и для условий вынужденного течения.
Модель кризиса представляется следующей. В условиях пузырькового режима кипения, ![]() , около поверхности нагрева имеется двухфазный граничный слой жидкость-пар, насыщенный паром. С возрастанием плотности теплового потока. увеличивается паропроизводительность и устойчивость жидких пленок, пронизывающих двухфазный граничный слой, нарушается. При значениях
, около поверхности нагрева имеется двухфазный граничный слой жидкость-пар, насыщенный паром. С возрастанием плотности теплового потока. увеличивается паропроизводительность и устойчивость жидких пленок, пронизывающих двухфазный граничный слой, нарушается. При значениях 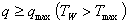 жидкая фаза отделяется от поверхности нагрева сплошным слоем пара. Происходит нарушение устойчивости двухфазного граничного слоя, существовавшего при пузырьковом кипении. При пленочном режиме кипения имеется двухфазный граничный слой, представляющий собой паровую пленку на поверхности нагрева и обтекающую ее массу жидкости. Указанный режим кипения может устойчиво существовать до тех пор, пока кинетическая энергия пара достаточна для поддержания во взвешенном состоянии масс жидкости, стремящихся под действием силы тяжести прорваться сквозь слой к поверхности нагрева.
жидкая фаза отделяется от поверхности нагрева сплошным слоем пара. Происходит нарушение устойчивости двухфазного граничного слоя, существовавшего при пузырьковом кипении. При пленочном режиме кипения имеется двухфазный граничный слой, представляющий собой паровую пленку на поверхности нагрева и обтекающую ее массу жидкости. Указанный режим кипения может устойчиво существовать до тех пор, пока кинетическая энергия пара достаточна для поддержания во взвешенном состоянии масс жидкости, стремящихся под действием силы тяжести прорваться сквозь слой к поверхности нагрева.
Гидродинамическая перестройка двухфазного пограничного слоя при пузырьковом кипении происходит при некоторой критической скорости парообразования ![]() . Можно сделать вывод, что
. Можно сделать вывод, что 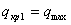 будет зависеть от поверхностного натяжения s, плотности пара
будет зависеть от поверхностного натяжения s, плотности пара ![]() теплоты парообразования L, подъемной силы
теплоты парообразования L, подъемной силы ![]() , где g ускорение силы тяжести,
, где g ускорение силы тяжести, ![]() плотность жидкости. Тогда по Кутателадзе выражение для максимальной плотности теплового потока имеет вид:
плотность жидкости. Тогда по Кутателадзе выражение для максимальной плотности теплового потока имеет вид:
![]() , (1.1)
, (1.1)
где С1=0,14. Зубер, используя неустойчивость поверхности раздела фаз по Гельмгольцу и Тейлору, аналитически получил выражение для ![]() с точностью до члена
с точностью до члена ![]() оказывающего существенное влияние при близких к критическому давлению Ркр.
оказывающего существенное влияние при близких к критическому давлению Ркр.
По Зуберу
![]() , (1.1)
, (1.1)
где К= 0,120![]() 0,157.
0,157.
Для второй критической плотности теплового потока ![]() по Кутателадзе вид формулы сохраняется, но меняется значение постоянной, при этом отношение
по Кутателадзе вид формулы сохраняется, но меняется значение постоянной, при этом отношение ![]() или
или ![]() .
.
2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
На данной экспериментальной установке изучается кризис кипения на горизонтальной платиновой проволоке d=20 мкм, помещенной в камеру с двуокисью углерода. Камера высокого давления 1 (рис. 2.1) из углеродистой стали представляет собой термостатируемый параллелепипед размерами 130´130´110 мм с цилиндрическим объемом d=50 мм и l=50 мм.
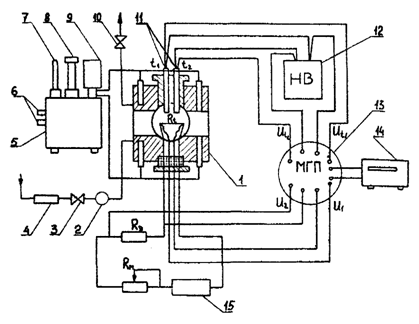
Рис.2.1. Общая схема установки:
1 рабочая камера; 2 манометр; 3 вентиль; 4 фильтр; 5 термостат U-1; 6 охлаждение термостата; 7 контрольный термометр; 8 контактный термометр с магнитной головкой; 9 мотор мешалки; 10 вентиль для продувки и откачки рабочего объема; 11 термопары для измерения температур внутри рабочего объема t1 и t2; 12 нуль-термостат "Нуль-В"; 13 многоточечный переключатель типа МГП-ТОМ; 4 универсальный вольтметр В7-21; 15 _ источник постоянного тока типа БП, 12 В, 0,6 А; Rэ эталонное сопротивление; Rэ=(0,9997±0,0003) 0м; Rt сопротивление платиновой проволоки; RM магазин сопротивлении Р33; Ut1, Ut2, U1, U2 - соответственно ЭДС термопар t1 и t2 и падения напряжений на платиновой нити и эталонном сопротивлении.
3. ПРОВЕДЕНИЕ И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА
3.1. Задание
3.1.1. Снять экспериментальную зависимость плотности теплового потока q (Вт/м) от средней температуры поверхности TW (°С) при кипении двуокиси углерода на платиновой проволоке по изобаре. Температура ТW, определенная из формулы (1.6), будет равняться средней, т. к. измеряется осредненное по длине проволоки сопротивление. Кривая должна иметь не менее 10-15 экспериментальных точек при повышении (прямой ход) и понижении (обратный ход) температуры проволоки (тока ее нагрева). Опытные данные представить графически в виде замкнутой координатной сетки.
3.1.2. Построить зависимость 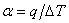 от средней температуры проволоки.
от средней температуры проволоки.
3.1.3. Рассчитать максимальную плотность теплого потока по формуле Кутателадзе-Зубера. (1.2). Значение К определить из графика зависимости ![]() комплекс D рассчитывается в условиях опыта. Сравнить экспериментальные данные по
комплекс D рассчитывается в условиях опыта. Сравнить экспериментальные данные по ![]() с теоретическими данными. Все физические параметры относить к температуре опыта.
с теоретическими данными. Все физические параметры относить к температуре опыта.
3.1.4, Экспериментальные значения 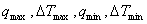 и расчетное
и расчетное ![]() внести в сводную таблицу данных.
внести в сводную таблицу данных.
3.1.5. Сделать выводы.
3.2. Проведение измерений и обработка экспериментальных данных
Перед проведением опыта по снятию кривой кипения необходимо провести измерение параметров U1 и U2 при температуре опыта с целью расчета сопротивления проволоки Rtж и величины R0
3.3.1. По достижении заданной температуры насыщения записали показания Ut1 Ut2 термопар t1 и t2 (переключаи давление насыщения.
Параметры насыщения в опыте
Температура насыщения ТS=(27,0±0,5) 0C;
Избыточное давление насыщения РS=(6860±20) кПа;
Падение напряжения на платиновой
нити U1=46,95 мВ;
U2=5,16 мВ.
3,3.2. На магазине сопротивления Р33 установим сопротивление RM=1999,9 0м. Измерить величины U1 и U2.
3.3.3. Вычислим сопротивление проволоки Rtж при заданной средней ТS;
![]() , (1.3)
, (1.3)
Rtж=(9,094±0,003) Ом.
R0 определяется выражением
![]() , (1.4)
, (1.4)
R0=(8,1±0,1) Ом.
где ![]() =4,33×10-3 0С-1 – температурный коэффициент сопротивления платины.
=4,33×10-3 0С-1 – температурный коэффициент сопротивления платины.
3.3.4. Вычислим сопротивление проволоки при всех значениях тока по формуле
![]() . (1.5)
. (1.5)
3.3.5. Средняя температура проволоки определяется формулой
![]() (1.6)
(1.6)
3.3.6. Вычислить плотность теплового потока
![]() , (1.7)
, (1.7)
где d=(20,0±0,1) мкм – диаметр платиновой проволоки;
l=(29,9±0,1) мкм – длина проволоки.
Рассчитанные значения опытных данных занести в таблицу 3.1.
3.3.7. Рассчитаем теоретическое значение плотности теплового потока при насыщении по формуле
![]() , (1.1)
, (1.1)
где К=0,15 - критерий определяется по графику (1.2) в методическом указании с учетом вычисленного 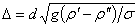 =0,05;
=0,05;
L=92,7 кДж/кг – теплота парообразования;
![]() =660,1 кг/м3 – плотность жидкого СО2;
=660,1 кг/м3 – плотность жидкого СО2;
![]() =285,4 кг/м3 – плотность паров СО2;
=285,4 кг/м3 – плотность паров СО2;
s=5,46×10-4 Н/м – поверхностное натяжение.
3.3.8. Расчет
Средние квадратические погрешности опытных значений ![]() , TS, РS (абсолютное давление). Результаты привести в табл. 3.2.
, TS, РS (абсолютное давление). Результаты привести в табл. 3.2.
Таблица 3.2
Сводная таблица экспериментальных данных
qmax, Вт/м2
теорет.
qmax, Вт/м2
опыт.
DТmax, 0С
qmin, Вт/м2
опыт.
DТmin, 0С
ТS, 0С
PS, кПа
Лабораторная работа №3
ВВЕДЕНИЕ
В работе рассматривается принцип действия теплопередающего устройства - тепловой трубы, проводятся испытания низкотемпературной тепловой трубы с раздельными каналами для пара и жидкости, оценивается ее эффективная теплопроводность.
1. ТЕОРИЯ
1.1. Основы работы тепловых труб
Самая простая по конструкции тепловая труба представляет собой герметично закрытую с концов тонкостенную трубку, внутренние стенки которой выложены слоем пористого материала - фитиля (сетками, пористыми материалами и т. д.).
Внутренняя полость трубки откачивается от газов до давления порядка 0.1 мм рт. ст., а затем фитиль пропитывается рабочей жидкостью(теплоносителем).
В трубе имеются три зоны: испарения, адиабатическая и конденсации. Подводимое в зоне испарения тепло передается за счет теплопроводности к теплоносителю. Испарение смачивающей фитиль жидкости приводит к образованию или увеличению кривизны вогнутых менисков на поверхности жидкости и в порах фитиля в зоне нагрева. Под действием сил поверхностного натяжения в вогнутых менисках появляется капиллярное давление ![]() , стремящееся уменьшить кривизну менисков. Капиллярное давление определяется формулой Лапласа:
, стремящееся уменьшить кривизну менисков. Капиллярное давление определяется формулой Лапласа:
![]() , (1.1)
, (1.1)
где R1, R2 - главные радиусы кривизны поверхности мениска, ![]() - коэффициент поверхностного натяжения.
- коэффициент поверхностного натяжения.
При испарении поглощается скрытая теплота парообразования, которая для жидкостей велика. Тепло переносится паром, который из зоны с высокой температурой и давлением движется в зону низкого давления, где конденсируется, выделяя ранее поглощенную теплоту парообразования.
Конденсация пара в зоне отвода тепла приводит к затоплению фитиля. Кривизна менисков жидкости внутри фитиля в этой зоне ничтожна по сравнению с кривизной в зоне нагрева трубы. Возникающая разница капиллярных давлений в этих двух зонах трубы приводит к перепаду давлений, который является движущим перепадом давления при перекачке жидкости по фитилю из зоны конденсации в зону испарения.
В любом сечении стационарно работающей трубы перепад давления между фазами (РП и РЖ) уравновешивается капиллярным давлением;
![]() , (1.2)
, (1.2)
где ![]() - перепад давления между паром и жидкостью вследствие фазового перехода.
- перепад давления между паром и жидкостью вследствие фазового перехода.
1.2. Тепловые трубы с раздельными каналами
В данной работе исследуется низкотемпературная ацетоновая тепловая труба с раздельными каналами, способная работать без больших температурных изменений при любой ориентации в гравитационном поле.
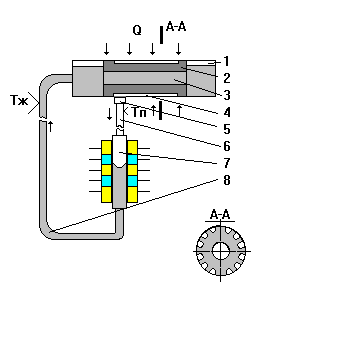
Рис. 1.1. Тепловая труба с раздельными каналами для пара и жидкости
1-испаритель; 2-фитиль; 3-компенсационная полость; 4-пароотводные каналы; 5-коллектор для пара; 6-основной паровой канал; 7- конденсатор; 8- жидкостной канал.
Основное уравнение для данных тепловых труб можно записать в виде:
![]() , (1.3)
, (1.3)
где ![]() - вязкостные потери давления в пароотводных каналах испарителя, в основном паровом канале, в жидкостном канале, в фитиле.
- вязкостные потери давления в пароотводных каналах испарителя, в основном паровом канале, в жидкостном канале, в фитиле.
Эти составляющие при ламинарном режиме течения на всех участках соответственно равны:
![]() , (1.4)
, (1.4)
где Q - тепловой поток, L - теплота парообразования, 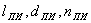 - длина, диаметр и число пароотводных каналов,
- длина, диаметр и число пароотводных каналов, ![]() - плотность и вязкость пара теплоносителя;
- плотность и вязкость пара теплоносителя;
![]() , (1.5)
, (1.5)
где ![]() - длина и диаметр парового канала;
- длина и диаметр парового канала;
![]() , (1.6)
, (1.6)
где ![]() - плотность и вязкость жидкого теплоносителя;
- плотность и вязкость жидкого теплоносителя; ![]() - длина и диаметр жидкостного канала;
- длина и диаметр жидкостного канала;
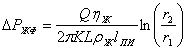 , (1.7)
, (1.7)
где К - проницаемость фитиля, r1 внутренний радиус компенсационной полости, r2 - наружный радиус фитиля.
Потери давления, обусловленные действием силы тяжести, определяют по формуле
![]() , (1.8)
, (1.8)
где g - ускорение свободного падения, lТТ - длина тепловой трубы, j - угол наклона тепловой трубы к горизонту.
Капиллярный напор равен
![]() , (1.9)
, (1.9)
где q - контактный угол или угол смачивания материала фитиля данной жидкостью; r - радиус кривизны мениска; К- кривизна мениска.
Потери давления на трение в фитиле классической тепловой трубы определяются по формуле
![]() . (1.10)
. (1.10)
2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Схема экспериментальной установки представлена на рис. 2.1. Тепловой поток к тепловой трубе подводится посредством электронагревателя. Питание подается через многоточечный переключатель от трансформатора. На паровом и жидкостном каналах расположены термопары, которые через многоточечный переключатель подключены к потенциометру типа ПП-63.
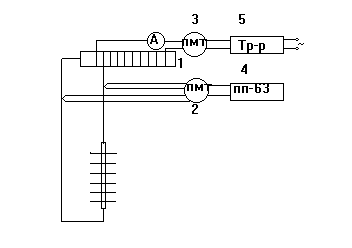
Рис. 2.1. Схема экспериментальной установки
1 - тепловая труба; 2-3 - переключатели; 4 - потенциометр; 5 - трансформатор.
3. МЕТОДИКА И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
3.1. Задание
3.1.1. Измерить температуру трубы при j=00 и j=900 при разных тепловых потоках (нагрузках).
3.1.2. Вычислить кривизну мениска и соответствующий ей радиус при этих ориентация для максимальной нагрузки.
3.1.3. Оценить эффективную теплопроводность тепловой трубы.
3.2. Основные параметры установки
3.2.1. Основные геометрические параметры установки приведены в таблице 3.1.
Таблица 3.1.
Основные параметры установки
Параметр
![]() , м
, м
![]() , м
, м
![]() , м
, м
![]() , м
, м
![]() , м
, м
![]() , м
, м
![]() , м
, м
![]() ,
,
м
![]() ,
,
м
![]()
К,
м2
Значение
1×10-3
5,4×10-3
3×10-3
5×10-2
2×10-1
6×10-1
5×10-1
1×10-3
0,6×10-2
1,4×10-2
1,27×10-2
3.3. Обработка результатов измерений
3.3.1. Для двух положений трубы при j=00 и j=900 при разных тепловых потоках измерили температуру жидкостного и парового каналов.
Так как нулевой спай термопар находится при температуре в лаборатории, то истинная температура трубы определяется по формуле
![]() , (3.1)
, (3.1)
где ![]() - температура найденная по градуировочной кривой;
- температура найденная по градуировочной кривой; ![]() =19 0С – температура в лаборатории.
=19 0С – температура в лаборатории.
Результаты измерений привели в таблице 3.2.
Таблица 3.2.
Температуры каналов трубы в зависимости от ориентации j
Угол
j=900
j=00
Q,
Вт
ЕП,
мВ
ЕЖ,
мВ
ТП,
0С
ТЖ,
0С
ЕП,
мВ
ЕЖ,
мВ
ТП,
0С
ТЖ,
0С
3.3.2. По результатам таблицы 3.2. построить графики зависимости ![]()
3.3.3. Оценить эффективную теплопроводность устройства по формуле
![]() , (3.2)
, (3.2)
где ТП – температура парового канала; ТЖ – температура жидкостного канала; 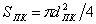 - поперечное сечение парового канала. Результаты расчетов заносим в таблицу 3.3.
- поперечное сечение парового канала. Результаты расчетов заносим в таблицу 3.3.
3.3.4. Найти вязкостные потери давления в трубе по формуле (1.3) используя формулы (1.4 – 1.8). Результаты расчетов занести в таблицу 3.3.
3.3.5. Вычислить кривизну мениска и соответствующий ей радиус для максимальной нагрузки при обеих ориентациях:
![]() ,
, ![]() (3.3)
(3.3)
Результаты расчетов занести в таблицу 3.3.
Таблица 3.3.
Расчет потерь давления, эффективной теплопроводности, кривизны и соответствующего ей радиуса мениска для максимальной нагрузки при обеих ориентациях тепловой трубы.
Угол
j=900
j=00
Пар
Жидкость
Пар
Жидкость
h, Н×с/м2
r, кг/м3
L×10-3, Дж/кг
s×103, Н/м
![]() , Вт/м×0К
, Вт/м×0К
![]() , Па
, Па
![]() , Па
, Па
![]() , Па
, Па
![]() , Па
, Па
![]() , Па
, Па
![]() , Па
, Па
К, 1/м
r, м
3.3.6. Используя формулу (1.10) определить вязкостные потери давления 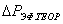 по жидкости в фитиле у классической тепловой трубы и найдем во сколько раз они превышают потери в используемой нами трубе.
по жидкости в фитиле у классической тепловой трубы и найдем во сколько раз они превышают потери в используемой нами трубе.
![]() =…,
=…,
![]() =…
=…
Лабораторная работа №5
ВВЕДЕНИЕ
В работе изучается теплоотдача в жидкость от тонкой проволочки, нагреваемой постоянным током. Измерения проводятся при свободном гравитационном режиме движения в стабильной и метастабильной областях.
1. ТЕОРИЯ
Гравитационным свободным движением (конвекцией) называют свободное движение под действием гравитационного поля в системе с неоднородным распределением плотности жидкости.
Современная математика не располагает еще достаточно общими аналитическими методами, которые позволили бы решать задачи конвективного теплообмена с той степенью приближении к действительности, которую требует практика. В подавляющем числе случаев для получения результатов, пригодных для непосредственного практического использования, приходится обращаться к эксперименту.
Однако и экспериментальное изучение процессов конвективного теплообмена значительно осложняется большим числом величин, оказывающих влияние на теплоотдачу. Поэтому приобретает большое значение предварительный теоретический анализ вопроса истодом подобия и методом размерностей. Такой анализ в конечном итоге приводит к уравнению подобия.
Как правило, гравитационную свободную конвекции рассматривают в условиях, когда размерю тела, вносящего тепловое возмущение, малы по сравнению 'с объемом окружающей его жидкости. В этом случае область теплового и гидродинамического возмущения оказывается локализованной около рассматриваемого тела. Вне этого пограничного слоя жидкость считается неподвижной.
На рис. 1.1 показан примерный вид распределения температуры Т и скорости v жидкости вблизи поверхности теплоотдающего цилиндра.
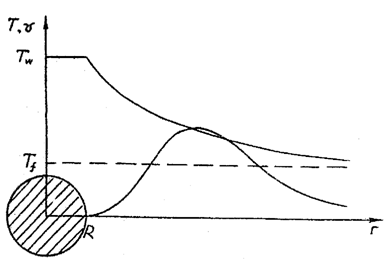
Рис. 1.1. Распределение температурыц Т и скорости v жидкости около нагретой проволочки:
TW – температура тела; Tf – температура жидкости на бесконечном удалении от тела
При инженерных расчетах теплоотдачи обычно имеют дело с двумя характерными задачами. В первой по известным значениям температуры тела Тw и температуры жидкости Тf определяют плотности теплового потока qw, а во второй задаче по известным значениям температуры жидкости и плотности теплового потока определяют температуру тела. Неизвестную величину плотности теплового потока qw от нагреваемой проволочки с радиусом R можно определить из закона Фурье-Остроградского:
![]() , (1.1)
, (1.1)
где l - коэффициент теплопроводности жидкости.
Закон Ньютона - Рихмана позволяет рассчитать коэффициент теплоотдачи a:
![]() . (1.2)
. (1.2)
Необходимое для вычисления производной в (1.1) распределение температуры Т возле нагретого цилиндра для стационарного случая может быть найдено из системы уравнений, включающей уравнение распространения тепла в движущейся жидкости, уравнение движения неоднородной нагретой жидкости (уравнение Навье - Стокса с учетом гравитации) и уравнение непрерывности. Система уравнений дополняется условиями однозначности (геометрическими, физическими, временными и граничными).
Проведя ряд упрощений и используя теорию подобия, система уравнений и граничные условия могут быть приведены к безразмерному виду. Анализ безразмерных соотношений позволяет найти числа подобия, характеризующие обе задачи, и уравнение подобия в общем виде
![]() (1.3)
(1.3)
Число Нуссельта ![]() является определяемым и характеризуется градиентом безразмерной температуры в потоке жидкости на поверхности нагрева. В первой характерной задаче, имеющей место в данной работе, задается температурный перепад
является определяемым и характеризуется градиентом безразмерной температуры в потоке жидкости на поверхности нагрева. В первой характерной задаче, имеющей место в данной работе, задается температурный перепад 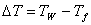 , и из уравнения (1.3) может быть определена плотность теплового потока qw на поверхности нити радиусом R. Число Грасгофа
, и из уравнения (1.3) может быть определена плотность теплового потока qw на поверхности нити радиусом R. Число Грасгофа ![]() характеризует относительную эффективность подъемной силы, вызывающей свободно-конвективное движение среды. Число Прандтля Pr=n/a - отношение интенсивности молекулярных переносов количества движения и тепла. В приведенных числах подобия используются следующие обозначения:
характеризует относительную эффективность подъемной силы, вызывающей свободно-конвективное движение среды. Число Прандтля Pr=n/a - отношение интенсивности молекулярных переносов количества движения и тепла. В приведенных числах подобия используются следующие обозначения:
g - ускорение свободного падения;
b - коэффициент объемного расширения жидкости;
n - кинематическая вязкость жидкости;
a - коэффициент температуропроводности жидкости.
Количественная связь между числами подобия обычно представляется в виде степенных зависимостей, например, в нашем случае
![]() . (1.4)
. (1.4)
Такая форма уравнений подобия является наиболее распространенной.
Параметры с и n соотношения (1.4) определяются экспериментально. При известных с и n соотношение (1.4) позволяет вычислить число Nu, а следовательно, и коэффициент теплоотдачи a для любого реального случая.
Уравнения (1.3) и (1.4) получены в предположении, что параметры жидкости l, n, a постоянны. При расчетах рекомендуется относить эти параметры к средней температуре ![]() .
.
![]() . (1.5)
. (1.5)
В зависимости от величины произведения Gr×Pr и формы тела параметры с и n в формуле (1.4) будут иметь разное значение. К примеру, в области 10-3< Gr×Pr<5×102 опытные данные слабо зависят от формы тела и удовлетворительно описываются формулой .
![]() . (1.6)
. (1.6)
При малом значении n согласно (1.4) зависимость ![]() близка к линейной. Коэффициент теплоотдачи a в условиях конвекции практически постоянен. Приведенные формулы справедливы только в режиме свободного гравитационного движения (без кипения). Увеличение плотности теплового потока выше соответствующей режиму пузырькового кипения приводит к изменению зависимости
близка к линейной. Коэффициент теплоотдачи a в условиях конвекции практически постоянен. Приведенные формулы справедливы только в режиме свободного гравитационного движения (без кипения). Увеличение плотности теплового потока выше соответствующей режиму пузырькового кипения приводит к изменению зависимости ![]() . Появление второй фазы (паровой), скрытый перенос его тепла от греющей поверхности, турбулизация всплывающими пузырьками пристеночного слоя приводят к резкому увеличению с ростом температуря коэффициента теплоотдачи при пузырьковом кипении.
. Появление второй фазы (паровой), скрытый перенос его тепла от греющей поверхности, турбулизация всплывающими пузырьками пристеночного слоя приводят к резкому увеличению с ростом температуря коэффициента теплоотдачи при пузырьковом кипении.
Вскипание жидкости на платиновой нити происходит при ее существенном перегреве. Это связано с тем, что фазовый переход жидкость-пар при температуре насыщения, соответствующей давлению в системе, происходит лишь при наличии протяженных обеих фаз. Если нагревать жидкость в отсутствии пара (как это имеет место в лабораторной работе), то ее вскипание возможно только при возникновении в ней пузырька пара критического размера, т. е. находящегося в равновесии с перегретой жидкостью. Размер критического зародыша изменяется от нескольких миллиметров вблизи линия насыщения до нескольких нанометров вблизи границы достижимого перегрева. Спонтанное зародышеобразование с заметной частотой происходит лишь при больших перегревах. Перегрев снижается при внесении в жидкость гетерогенных центров зародышеобразования. Такими центрами могут служить микропузырьки газа, плохо смачивающиеся участки твердой поверхности и т. д. На платиновой нити бензол в пристеночном слое удается перегреть на 80-100 и более градусов.
Свойства перегретой жидкости изменяются также и монотонно с температурой, как и в стабильной области. Поэтому в метастабильной области также справедливо соотношение (1.4).
По экспериментальной зависимости 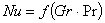 (или
(или ![]() ) можно определить постоянные с и n в формуле (1.4). Это и является задачей данной лабораторной работы.
) можно определить постоянные с и n в формуле (1.4). Это и является задачей данной лабораторной работы.
2. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
В настоящей работе изучается теплоотдача от тонкой проволочки в жидкий бензол. Схема установки приведена на рис. 2.1.
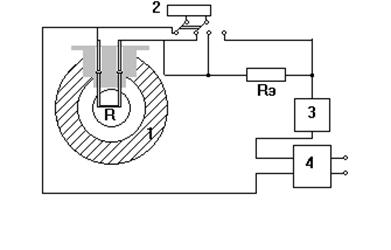
Рис. 2.1. Схема установки.
1 – камера; 2 – цифровой вольтметр; 3 – магазин сопротивлений; 4 – источник питания; R – платиновая проволочка; RЭ – образцовое сопротивление.
3. МЕТОДИКА И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
3.1. Задание
3.1.1. При комнатной температуре жидкости в камере и атмосферном давлении измерить и нанести на график зависимость плотности теплового потока qW от разности температур проволочки и жидкости.
3.1.2. По опытным данным рассчитать и построить в логарифмическом масштабе график зависимости числа Нуссельта от комплекса (Gr×Pr) и найти по этой зависимости параметры уравнения подобия c и n.
3.2. Параметры установки
Основные параметры установки приведены в таблице 3.1.
Таблица 3.1.
Параметры экспериментальной установки
Параметр
Обозначение
Единицы измерения
Значение
Эталонное сопротивление
RЭ
Ом
(2,980±0,001)
Площадь боковой поверхности нити
Sбок
м2
0,992×10-6
Радиус нити
r
м2
1,0×10-5
3.3. Обработка опытных данных
3.3.1. Измерим температуру жидкости в камере
Тf=20,9 0C=294,05 0К.
3.3.2. Для измерения плотности потока тепла в жидкость и температуры проволочки на магазине сопротивлений последовательно выставляем значения RM равные 100, 75, 50, 40, 24, 20 и 14 Ом. Измеряем соответствующие падения напряжения на проволочке и образцовом сопротивлении U и UЭ соответственно. Данные заносим в таблицу 3.2.
3.3.3. Вычислим коэффициент теплоотдачи a в бензол для всех проведенных опытов по формуле
![]() , (3.1)
, (3.1)
где 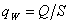 - плотность теплового потока;
- плотность теплового потока;
S – площадь поверхности проволочки
![]() =9,923×10-7, м2;
=9,923×10-7, м2;
![]() - мощность выделяемая на нити;
- мощность выделяемая на нити;
TW=-33,174+68,969×R – температура нити и ее градуировочная зависимость от сопротивления нити.
Результаты расчетов заносим в таблицу 3.2.
Таблица 3.2.
Сводная таблица экспериментальных данных для нахождения a
N
Rм, Ом
U, В
UЭ, B
R, Ом
TW, 0K
DT, 0K
Q, Вт
qW, Вт/м2
a, 103 Вт/м2×0К
1
100
2
75
3
50
4
40
5
24
6
20
7
14
3.3.4. Вычислим числа подобия Nu, Gr, Pr для средней температуры ![]() .
.
Число Нуссельта находим по формуле
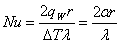 . (3.2)
. (3.2)
Число Грасгофа вычисляем по формуле
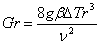 . (3.3)
. (3.3)
где ![]() - кинематическая вязкость жидкости;
- кинематическая вязкость жидкости;
b=1,06×10-3, 0К – коэффициент объемного расширения.
Число Прандтля получается из соотношения
![]() , (3.4)
, (3.4)
где 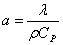 - коэффициент температуропроводности.
- коэффициент температуропроводности.
Значения величин 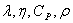 вычисляются с помощью аппроксимационных полиномов.
вычисляются с помощью аппроксимационных полиномов.
Коэффициент теплопроводности бензола
![]() , (3.5)
, (3.5)
а0=… а1=… а2=… а3=…;
средняя температура в оС.
Вязкость бензола
![]() , (3.6)
, (3.6)
а0=… а1=… а2=… а3=…;
средняя температура в оС.
Теплоемкость бензола
![]() , (3.7)
, (3.7)
а0=… а1=… а2= ... а3=…
средняя температура в оК.
Плотность бензола
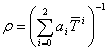 , (3.8)
, (3.8)
а0=… а1=… а2=…;
средняя температура в оС.
3.3.5. Прологарифмируем числа Нуссельта Nu и комплекс (Gr×Pr). Результаты расчетов заносим в таблицу 3.3.
Таблица 3.3.
Данные для построения графика lg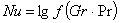
N
![]() , 0К
, 0К
lg(Gr×Pr)
lg(Nu)
1
2
3
4
5
6
7
3.3.6. Постоить график зависимости lg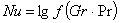 и отметим точку перехода через линию насыщения.
и отметим точку перехода через линию насыщения.
3.3.7. Для определения с и n в формуле 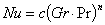 обработать экспериментальные данные методом наименьших квадратов в режиме без кипения.
обработать экспериментальные данные методом наименьших квадратов в режиме без кипения.
Построить график зависимости lg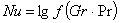 в режиме без кипения обработанный методом наименьших квадратов.
в режиме без кипения обработанный методом наименьших квадратов.
Уравнение прямой lgNu=lgc+n×lg(Gr×Pr) откуда находим коэффициенты подобия с и n с учетом ошибок




