Математический кружок 7 класс
Решения занятия №20 Проценты.
Процент – это другое название сотой части числа, т. е. когда говорят 1% от х, понимают 0,01 часть числа х, равную 0,01х. В решениях задач часто не удобно пользоваться процентами, поэтому их заменяют на части числа.
Например, было k конфет, съели 20% конфет, т. е. съели 0,2 часть конфет, или 0,2k, осталось 80% или 0,8k.
Первые три задачи (разобранные в классе).
1. За первый год население некоторой деревни возросло на n человек, а за второй — на 300 человек. При этом за первый год население увеличилось на 300%, а за второй — на n%. Сколько жителей стало в деревне?
Ответ. 500.
Решение 1. Пусть изначально жителей в деревне было х, тогда за год число жителей в деревне стало х+n, а после второго х+n+300 человек. Известно, что за первый год число жителей увеличилось на 300%, т. е., так как 300% от х – это 3x, то n=3x. Так же известно, что за второй год число жителей увеличилось на n%, т. е. на ![]() . Т. к. население увеличилось на 300 человек, то
. Т. к. население увеличилось на 300 человек, то 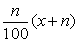 =300, зная, что n=3x, получим: 10000 = 4х2, значит х=50. После второго года число жителей в деревне стало х+n+300=4x+300=200+300=500.
=300, зная, что n=3x, получим: 10000 = 4х2, значит х=50. После второго года число жителей в деревне стало х+n+300=4x+300=200+300=500.
Решение 2. Пусть изначально жителей в деревне было х, возросло на 300%, т. е. на 3x, значит, стало равно x+3x=4x. За второй год количество жителей выросло еще на n%, так как n% от 4x это ![]() , то жителей стало 4x+
, то жителей стало 4x+![]() .
.
По условию за первый год количество людей увеличилось на n человек, значит, n=3x. Во второй год количество людей увеличилось на 300 человек, значит 300=![]() . Подставляя n=3x во второе равенство получаем 300=
. Подставляя n=3x во второе равенство получаем 300=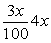 . Преобразуем: 1002=4x2 т. е. 1002=(2x)2. Откуда x=50.
. Преобразуем: 1002=4x2 т. е. 1002=(2x)2. Откуда x=50.
2. Лёша, Тоша и Гоша кушали пряники. Лёша съел на 10% больше пряников, чем Тоша. А Гоша на 20% больше, чем Лёша. Во сколько раз Гоша скушал больше пряников, чем Тоша?
Ответ. В 1,32 раза.
Решение. Пусть Тоша съел х пряников, тогда Леша съел 1,1х пряников и Гоша съел 1,2×1,1х=1,32х пряников. Таким образом, Гоша съел в 1,32 больше пряников, чем Тоша.
3. Хомяк сидит на диете. Каждый день он съедает 20% имеющихся к этому дню защёчных запасов. Изначально за обеими щеками у него спрятано поровну запасов. Через сколько дней все запасы поместятся за одну щёку?
Ответ. Через 4 дня.
Решение. Пусть изначально у хомяка всего х запасов, за одну щеку помещается х/2 запасов. Выясним, когда количество защёчных запасов хомяка окажется меньше х/2 (или равно х/2). После первого дня у хомяка останется 0,8х запасов, что больше х/2. После второго 0,8×0,8х=0,64х запасов, что тоже больше х/2. После третьего дня, количество запасов у хомяка станет 0,8×0,64х=0,512х, т. е. по-прежнему больше х/2. После четвертого дня количество запасов станет 0,8×0,512х=0,4096<х/2, значит, после четвертого дня хомяк сможет поместить остатки своих защечных запасов за одну щеку.
Задачи для самостоятельного решения.
1. Посевной участок под бурьян имеет прямоугольную форму. В рамках реструктуризации одну сторону участка увеличили на 20%, а другую уменьшили на 20%. Изменится ли в результате урожай бурьяна, и если изменится, то как?
Ответ. Урожай уменьшится на 4%.
Решение. Пусть длина одной стороны участка – a, другой – b. Тогда площадь S=ab. Пусть сторона a увеличилась на 20%. Тогда она увеличилась на 0,2a то есть стала равно 1,2a. Сторона b уменьшилась на 20%. Значит она уменьшилась на 0,2b и стала равной 0,8b. Площадь нового участка будет равна: Sн=1,2a×0,8b=0,96ab, т. е. 96% от первоначальной площади.
2. Цены на плюшевых мишек в октябре выросли на 50%, а перед Новым годом на них объявили 50% скидку. Когда мишка стоил дороже – 1 сентября или 31 декабря?
Ответ. 1 сентября.
Решение. Пусть 1 сентября мишка стоил х, в октябре стоимость мишки увеличилась на 50%, и стала х+0,5х=1,5х. Перед Новым годом цена на мишек уменьшилась на 50% и стала 1,5х-0,5×1,5х=1,5х-0,75х=0,75х, что составляет 75% от цены сентября.
3. Мама купила ирисок в три раза больше, чем леденцов. Федя накинулся на ириски и съел 20% ирисок, а Маша – на леденцы – и съела 10% леденцов. Какой процент конфет съели дети?
Ответ. 17,5% от всех конфет.
Решение. Пусть леденцов было х, тогда ирисок 3х, т. е. всего конфет 4х. Федя съел 20% ирисок, т. е. съел 0,2×3х=0,6х конфет. Маша съела 0,1х конфет, т. е. всего было съедено 0,7х конфет. Так как всего конфет 4х, то дети съели 0,7х÷4x=0,175 от всех конфет или 17,5% всех конфет.
4. В семье 4 человека. Если Маше удвоят стипендию, общий доход всей семьи возрастет на 5%, если вместо этого маме удвоят зарплату - на 15%, если же зарплату удвоят папе - на 25%. На сколько процентов возрастет доход всей семьи, если дедушке удвоят пенсию?
Ответ. 55%.
Решение. Если Маше удвоят стипендию, семейный доход возрастёт на размер этой стипендии. Следовательно, Машина стипендия составляет 5% общего дохода. Аналогично, мамина зарплата составляет 15%, а папина – 25%. Оставшаяся доля 100%-5%-15%-25%=55% приходится на дедушкину пенсию. Значит, если ему удвоят пенсию, доход всей семьи возрастёт на 55%.
Это же решение можно сформулировать по-другому. Если бы всем членам семьи вдруг стали платить вдвое больше, общий доход увеличился бы на 100%. Из этих 100 процентов 5 приходится на Машу, 15 – на маму, 25 – на папу, а остальные 55 – на дедушку.
5. В 7 "Г" классе хватает двоечников, но Вовочка учится хуже всех. Педсовет решил, что либо Вовочка должен к концу четверти исправить двойки, либо его исключат. Если Вовочка исправит двойки, то в классе будет 24% двоечников, а если его выгонят, то двоечников станет 25% . Какой процент двоечников в 7 "Г" сейчас?
Ответ. 28%
 Решение. Пусть в классе n человек, из них k двоечников (считая Вовочку). Если Вовочка исправит двойки, то в классе останется k-1 двоечник – по условию это 24%, т. е.
Решение. Пусть в классе n человек, из них k двоечников (считая Вовочку). Если Вовочка исправит двойки, то в классе останется k-1 двоечник – по условию это 24%, т. е.
0,24n=k-1 (1).
Если Вовочку выгонят, то в классе останется n-1 человек и из них k-1 двоечник – по условию это 25%, т. е.
0,25(n-1)=k-1 (2).
В равенствах (1) и (2) правые части равны, значит можно приравнять левые части: 0,24n=0,25(n-1), откуда 0.01n=0.25, то есть n=25. Подставим это значение в равенство (1) и найдем k: k=7. Значит сейчас в классе k/n * 100% = 28% двоечников.
6. Крокодил Гена погружался на дно. Вначале он погрузился на 1 метр и испугался. Потом он набрался храбрости и преодолел еще половину оставшейся глубины. Затем, после небольшой передышки, он погрузился еще на 1 метр. До дна уже оставалось 30% всей глубины. На какую глубину погружался Гена?
 Ответ. 7,5 метров.
Ответ. 7,5 метров.
Решение. Пусть вся глубина x, тогда Сначала Гена погрузился на 1 метр, а потом на половину оставшегося пути, т. е. на (х-1)/2, затем Гена погрузился еще на 1 метр и осталось до дна 30% т. е. 0,3х. Составим уравнение: 1+(х-1)/2+1+0,3х=х, откуда х=7,5.
7. Все акции компаний «Карабас» и «Барабас» вместе стоят 90 золотых монет. У Буратино есть 25% акций компании «Карабас» и 75% акций компании «Барабас» общей стоимостью 30 золотых монет. Найдите стоимость всех акций каждой компании.
Ответ. Все акции компании «Карабас» стоят 75 монет, а все акции компании «Барабас» стоят 90-75=15 монет.
Решение. Пусть все акции компании «Карабас» стоят х монет, тогда все акции компании «Барабас» стоят 90-х монет, так как вместе акции компаний «Карабас» и «Барабас» стоят 90 монет. У Буратино есть 25% акции «Карабас», стоимостью 0,25х, и 75% акций компании «Барабас», стоимостью 0,75(90-х). Всего у Буратино акций на 30 монет, значит 0,25х+0,75(90-х)=30. Решив это уравнение, получим х=75, значит все акции компании «Карабас» стоят 75 монет, а все акции компании «Барабас» стоят 90-75=15 монет.
8. Курс акций компании "Рога и копыта" каждый день в полдень повышается или понижается на 17 процентов (курс не округляется). Может ли курс акций дважды принять одно и то же значение?
Ответ. Не может.
Решение. Заметим, что при повышении курса акций он умножается на ![]() , а при понижении -- на
, а при понижении -- на ![]() . То есть если курс акций был равен x, то после k повышений и l понижений курс акций станет равным
. То есть если курс акций был равен x, то после k повышений и l понижений курс акций станет равным ![]() . Если
. Если ![]() , то
, то ![]() . Но в правой части этого равенства стоит четное число, а в левой -- нечетное. Противоречие.
. Но в правой части этого равенства стоит четное число, а в левой -- нечетное. Противоречие.




