Задачи использования информационных технологий на уроках математике

– учитель математики

Цель моей работы формирование целостной системы универсальных знаний, умений и навыков; развитие личности школьника по средствам изучении предметов с использованием информационно – коммуникационных технологий.

Задачи использования информационных технологий на уроках математике:

1.  Усиление мотивации учения;

2.  Индивидуализация и дифференциация учебного процесса при сохранении его целостности;

3.  Сделать усвоение знаний эффективными и интересными для ученика;

4.  Интенсифицировать процесс обучения, сделать его более наглядным и динамичным.

Для того, чтобы учащиеся овладели системой математических знаний и умений, необходимо очень серьёзно относится к обобщению и систематизации получаемых знаний по каждой теме, всему курсу обучения. Я занимаясь исследовательской и экспериментальной деятельностью в течение ряда лет и пришла к заключению, что далеко не всегда учитель уделяет серьёзное внимание систематизации знаний учащихся. Большую часть своих усилий он направляет на то, чтобы добиваться запоминания учебной информации, выполнения заданий по алгоритму, образцу и подобию.

Для современных школьников это не срабатывает. Они другие: энергичные, инициативные, жаждущие деятельности. Поэтому надо искать новые формы и методы. И я думаю, что с помощью средств ИКТ можно выстроить учебный процесс так, что ученикам станет интересно, а учитель сможет решить поставленные выше дидактические задачи.

Поэтому на своих уроках я использую различные мультимедийный курсы, но подробнее хочу остановиться на иллюстрации данного мультимедийного курса «Открытая Математика 2.6. Функции и графики» которые позволяет доступно ученикам освоить следующие темы данной дисциплины: системы координат, основные свойства функций, преобразование графиков функций в декартовой системы координат.

Курс располагает всеми возможностями для получения учащимися обширных знаний по математике в наглядной интерактивной форме. Так например:

ü  Интерактивная модель демонстрирует понятие декартовой системы координат на примере известной игры «Морской бой».

ü  В модели свойства функции демонстрируются различные понятия, связанные с анализом функций: области определения и значений, нули функции, промежутки монотонности и знакопостоянства, критические точки и точки перегиба, асимптоты и другие понятия,

ü  Интерактивная модель «Преобразование графиков функций» является фактически комбинацией трех моделей «Параллельный перенос графиков», «Сжатие и растяжение графиков», «Отражение графиков относительно осей и точек»,

ü  построение графиков функций используя графер.

Данный курс является незаменимым помощником для подготовки к сдачи ЕГЭ, для создания рефератов и творческих работ, проектов.

Так же интерактивный курс предусматривает возможность ученикам использовать его как при самостоятельном обучении дома, так и во время занятий в компьютерном классе.

Одно из направлений использования компьютера на уроках – проведение обобщения по теме с использованием презентации и мультимедийного курса «Открытая Математика 2.6. Функции и графики», который прекрасно иллюстрирует построение графиков и их преобразование.

Вашему вниманию предлагается пример проведения урока с использованием мультимедийного курса «Открытая Математика 2.6. Функции и графики».

Разработка урока по теме: «Графики функций ».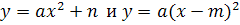

Урок проводится в компьютерном классе, каждый ученик сидит за персональным компьютером, на котором установлен мультимедийный курс «Открытая Математика 2.6.Функции и графики».

Цель урока: закрепление, обобщение и систематизация знаний по теме «Графики функций 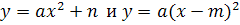», формирование навыков построения графиков функций 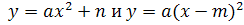и навыков работы с мультимедийным курсом «Открытая Математика 2.6.Функции и графики».

Задачи урока:

1. Обучающие:

·  Закрепление, обобщение и систематизации знаний полученных при изучении темы из курса алгебры 9 – го класса - «Графики функций

».

·  Применение мультимедийного курса «Открытая Математика 2.6.Функции и графики» к построению функций графиков вида

·  Выработка умения применять теоретические знания при решении конкретных задач.

·  Формирование навыков экспериментально-исследовательской и аналилитической деятельности.

2.Воспитывающие:

·  Воспитание культуры труда,

·  Воспитание аккуратности при выполнении практической работы;

·  Воспитание у учащихся мотивации учебной деятельности;

·  Воспитание ответственности, целеустремлённости;

·  Формирование навыков работы в парах;

·  Выработка принципов взаимоконтроля.

3. Развивающие:

·  Развитие мышления, памяти, внимания, умения сопоставлять и анализировать, собранности;

·  Продолжить развитие навыков работы на компьютере; интереса к предметам математика и информатика.

Методы работы: фронтальный опрос, практический, индуктивный, проблемно – поисковый метод самостоятельной работы, работа с мультимедийным курсом «Открытая Математика 2.6.Функции и графики».

Оборудование к уроку:

Ø  Компьютерный класс;

Ø  Экран;

Ø  Мультимедиапроектор, компьютер;

Ø  Мультимедийный курс «Открытая Математика 2.6.Функции и графики»;

Ø  Шаблоны: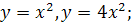

Ø  Цветные карандаши (синий, зелёный, красный, бирюзовый, фиолетовый);

Ø  Учебник;

Ø  Тетрадь;

Ø  Линейка.

Ход урока:

1.Начальный этап урока:

1) Организационный момент: проверка готовности учеников к уроку, отмечаем отсутствующих учеников. Дежурные собирают тетради с домашней работой.

2) Тема сегодняшнего урока - «Графики функций 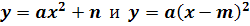» (приложение 1)

3) Цель урока – формирование навыков построения графиков функций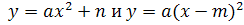 и навыков работы с мультимедийным курсом «Открытая Математика 2.6.Функции и графики».
4) Перейдём к устным упражнениям.

Обратимся к слайдам 2, 3 (приложение 2, 3) и ответим на вопросы.

1.  Сформулируйте определение квадратичной функции.

2.  Сформулируйте свойства квадратичной функции :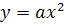

а) при а>0;

б) при а<0.

3.Как из графика функции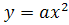 можно получить график функции 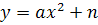; график функции ?

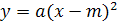4. Как из графика функции 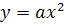можно получить график функции ?

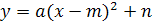5. № 95 ( по учебнику).

2. Основная часть урока:

·  Одной из обучающих задач урока, является Формирование навыков экспериментально-исследовательской и аналилитической деятельности.

На реализации этой задачи в ходе урока я хочу подробно остановится в основной части урока.

1)  Тренировочные упражнения (приложение 4):

Начинаем работу за персональным компьютером.

№91 (в, г) – самостоятельно в тетради с последующей проверкой по граферу (использовать шаблон ).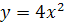

1)  Постройте самостоятельно в тетради график функции

в)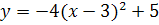 (синим цветом), г) 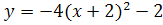(красным цветом) используя шаблон .

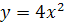ИССЛЕДОВАНИЕ:

Вывод: Какую исследовательскую работу вы должны были выполнить чтобы построить данные графики?

1)Куда направлены ветви параболы?

Ветви направлены вниз;

2)С помощью каких преобразований выполнено построение графиков? Параллельным переносом по оси х и по оси у;

[в) по оси х вправо на 3 ед; по оси у вверх на 5ед.; г)по оси х влево на 2 ед; по оси у вниз на 2 ед.]

3)Какая координата вершины параболы получилась?

Координаты вершин парабол; [в)(3;5)-вершина; г)(-2;-2) – вершина].

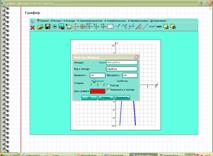
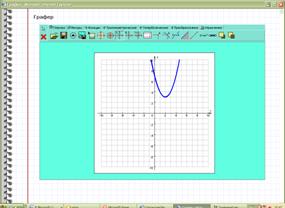
2) Вспомним, как с помощью графера выполнить эту проверку.

Выполняем проверку одновременно с учителем.

1)Открываем графер

2)  Высвечивается координатная плоскость

3)  Перейти на английский язык. Вводим функцию в) ;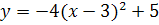

4)Получили график функции

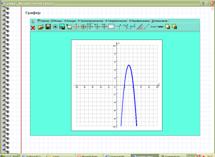
Сравниваем график функции на графере с графиком функции в тетради.

Ученики делают вывод:

1) ветви направлены вниз;

2) (3;5) – вершина

3) параллельный перенос а) по оси х вправо на 3 ед; б) по оси у вверх на 5 ед ;

Проверяем г) 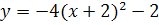(красным цветом)

Нажимаем на координатную плоскость высвечивается окошечко для ввода функции

Получили график функции 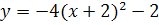(красным цветом)

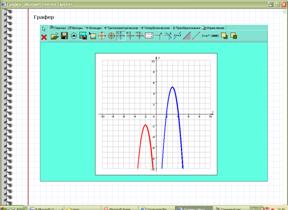
Сравниваем график функции на графере с графиком функции в тетради.

Ученики делают вывод:

1) ветви направлены вниз;

2) (-2;-2) – вершина

3) параллельный перенос а) по оси х влево на 2 ед;б) по оси у вниз на 2 ед ;

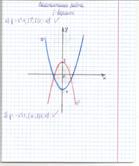
№ 93 – самостоятельно с последующей проверкой по граферу.

Ученики в тетрадях строят графики, функций используя шаблон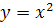 (учитель заранее говорит цвета графиков)

а) 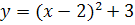(синим цветом);

б) 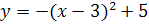(красным цветом).

А потом работают с графером самостоятельно и проверяют свою работу. При необходимости учитель оказывает помощь.

а) 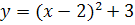(синим цветом);

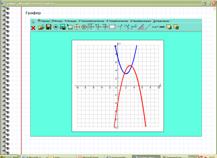
б) 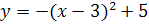(красным цветом).

Сравниваем график функции на графере с графиком функции в тетради.

А)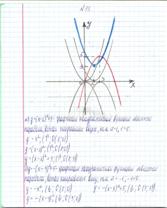

Как построили графики?

Ученики сделали вывод: а)определили направление ветвей(вверх) и координаты вершины параболы(2, 3) б) определили направление ветвей(вниз) и координаты вершины параболы(3, 5).

Как построить график функции ?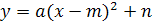

Итак делаем вывод: для построение графика функции

Достаточно определить направление ветвей параболы и координату вершины.

Если а>0, то ветви направлены вверх.

Если а<0, то ветви направлены вниз.

(m, n)-вершина параболы.

Самостоятельная работа (приложение 5).

Вариант № I.

Вариант № II.

Используя шаблон параболы , постройте график функции.

а) ;

б);

в);

г) ;

д) .

а);

б);

в);

г) ;

д) .

а) Ученики строят графики заданными цветами, указанными на слайде.

Обратимся к слайду работа ученика в тетради

I вариант

б) Меняются тетрадями и проверяют работы, используя графер.

Обратимся слайду проверка

I вариант:

А)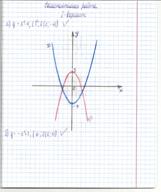

II вариант:

Обратимся к слайду работа ученика в тетради

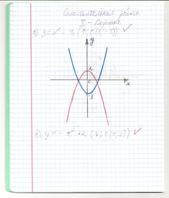
Меняются тетрадями и проверяют работы, используя графер.

Обратимся слайду проверка

А)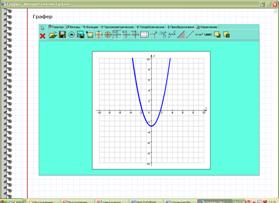

Оценивают сами. Критерий оценки показан на слайде 6 (приложение 6).

Разбор типичных ошибок, допущенных по ходу самостоятельной работы.

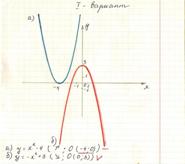
а) неверно определены координаты вершина параболы.

б) выполнено всё верно.

в) неверно определены координаты вершина параболы.

г) неверно определена координаты вершина параболы и направление ветвей параболы.

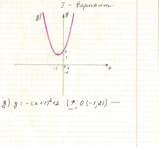
д) неверно определены направления ветвей параболы.

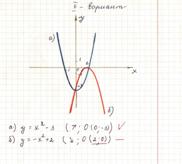
а) выполнено, верно

б) неверно определены координаты вершина параболы

в) неверно определена координаты вершина параболы

г) верно определены координаты вершины параболы, но записано неверно.

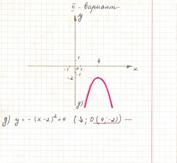
д) неверно определены координаты вершины параболы.

Выставление оценок;

Работы собираются учителем.

3.Заключительный этап урока:

1) Итог урока:

Ø  Подводим итог урока: Как мы работали?(вопрос ученикам)На сегодняшнем уроке мы научились строить графики функций вида 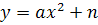, , 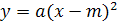, 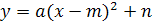с помощью шаблонов и проверять свои графики, используя мультимедийный курс «Открытая Математика 2.6.Функции и графики».

2) Домашнее задание (слайд 7) (приложение 7):

п. 6, №87 (б, в), № 92, № 99 (в, г), № 84, № 85.

Нас интересует результаты данной самостоятельной работы, обратимся к таблице результатов успеваемости и качества знаний учащихся.

В классе

18

100%

Писало

18

100%

Выполнили работу на оптимальном уровне

10

56%

Допустили 1 ошибку

5

28%

Допустили 2 ошибки

3

16%

Успеваимость:100%

Качество знаний: 83%

«5» - 10; «4» - 5; «3» - 3; «2» - 0.

Мнение родителей:

От родителей до меня дошла информация, что дети любят такие уроки, идут на них с удовольствием.

Спасибо за урок.