УДК 620.179.15:681.3.06
,
Институт проблем регистрации информации НАН Украины
ул. Н. Шпака, 2, 03113 Киев, Украина
Объемная реконструкция «больших» объектов
на томографах с ограниченной по размерам
матрицей детекторов
Рассмотрены вопросы объемной реконструкции «больших» объектов на томографах с ограниченными по размерам матрицами детекторов. Показана целесообразность применения в качестве детекторов высокого разрешения рентгенооптических преобразователей с цифровыми видеокамерами. Использована модификация алгоритма Фельдкампа для цилиндрической матрицы детекторов, регистрирующей только часть прошедшего через объект излучения. Предложены способы повышения точности реконструкции.
Ключевые слова: компьютерная томография, объемная реконструкция, конусный пучок, матрица детекторов, рентгенооптический преобразователь, цифровая видеокамера.
Информацию о внутренней структуре объекта можно получить при помощи сканирований ряда сечений (2D) рентгеновскими веерными лучами с последующей их регистрацией линейкой детекторов (1D). Алгоритмы 2D реконструкции для веерных лучей обеспечивают отличное качество восстановления. К сожалению, такой подход при сканировании протяженных объектов не может обеспечить высокую производительность исследований [1, 2].
Переход от регистрации веерных лучей линейкой детекторов к регистрации матрицей детекторов конусного пучка рентгеновского излучения позволяет весьма существенно (на несколько порядков) увеличить число одновременно регистрируемых лучей, ранее при веерном пучке удаляемых коллиматором. Это кардинально сокращает время сбора данных. Внедрению томографов с веерным пучком способствовало появление сравнительно дешевых двумерных матриц детекторов на основе рентгенооптического преобразователя и цифровой видеокамеры на основе ПЗС структур. Двумерные матрицы детекторов на основе рентгенооптического преобразователя и цифровой видеокамеры обладают высоким пространственным разрешением (до 4096×4096 пикселов) и чувствительностью, а также дают возможность регистрировать рентгеновское излучение в широком динамичес-
© ,
ком диапазоне (28…216). Пожалуй, основным недостатком таких матриц детекторов следует считать ограниченность размера входного окна рентгенооптического преобразователя, что не обеспечивает полноту регистрации проекционных данных при сканировании объектов диаметром свыше 200–300 мм.
Рассширение сферы применения томографов промышленного назначения для объемного сканирования объектов большего диаметра стало насущной задачей. Впервые в январе 2002 г. системы неразрушающего контроля TOMOHAWK фирмы YXLON International [3] получили программное обеспечение, позволяющее выполнять реконструкцию объектов значительно большего диаметра, чем это было возможно ранее.
В ИПРИ в этот же период велись работы в данном направлении. Были разработаны алгоритмы объемной реконструкции «больших» объектов в конусных пу-чках в системах сканирования с равномерным расположением детекторов как на плоскости [4], так и на поверхности цилиндра с центром в фокусе излучателя. Расположение детекторов на ограниченной по размерам цилиндрической поверхности позволяет упростить процесс реконструкции и повысить ее качество.
(1)
Объемная реконструкция «больших» объектов при использовании таких детекторов и вращения объекта вокруг соответственного центра (одного или нескольких центров) может быть выполнена по модифицированному алгоритму Фельдкампа для цилиндрического детектора. Реконструкция плотности объекта в точке (x, y, z) определяется выражением [1]: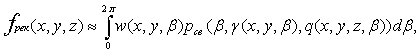
(2)
где b — угол, определяющий взаимное положение источника излучения и объекта; w(x, y, b) — весовой множитель, учитывающий расстояние от источника излучения b до проекции точки (x, y, z = 0) на плоскость вращения L(x, y, b)![]()
Величина весового множителя w(x, y, b) определяется соотношением
![]()
(3)
где g(x, y, b) — угол между проекцией луча на центральную плоскость вращения и центральным лучом. Луч из источника в положении b проходит через точку (x, y, z) и пересекает цилиндрический детектор. Угловая координата равна
![]()
(4)
где q(x, y, z, b) — координата точки пересечения рассматриваемого луча по высо-
те ряда цилиндрического детектора
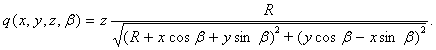
(5)
Основная проблема реконструкции «больших» объектов заключается в получении достаточно высокого качества свернутых проекций. Объемная реконструкция «больших» объектов имеет много общего с веерной реконструкцией широких объектов. Тем не менее, между ними имеются и существенные различия. Прежде всего, модифицированный метод Фельдкампа, в отличие от точного метода веерной двухмерной реконструкции, является приближенным. Расходимость лучей конусного пучка при частичном (предположим, половинном) охвате объекта по ширине приводит к тому, что в свертке для слоев, отличных от центрального, будут участвовать лучи, лежащие в различных плоскостях (точнее — линейчатых поверхностях). Это обстоятельство оказывает сильное влияние при сканировании объектов резко асимметричных относительно центра вращения. При этом целесообразно произвести два сканирования объекта вокруг двух центров вращения. В общем случае для более широких объектов для полного сбора данных может понадобиться больше сканирований (n > 2) вокруг соответствующих n центров вращения.
Рассмотрим результаты реконструкции стандартного фантома Шеппа–Логана при различных условиях сканирования, параметры которого приведены в таблице.
Фантом Шеппа–Логана состоит из 12 эллипсоидов с координатами центров (cx, cy, cz) и полуосями (rx, ry, rz), также показаны значения углов поворота в градусах вокруг оси «y» эллипсоидов и значения их плотностей.
Параметры фантома Шеппа–Логана
Эллипс
cx
сy
cz
rx
ry
rz
градус
плотность
1
0,000
0,000
0,000
0,690
0,900
0,920
0,000
2,000
2
0,000
0,000
–0,018
0,662
0,880
0,874
0,000
–0,098
3
–0,220
0,250
0,000
0,410
0,210
0,160
–72,00
–0,020
4
0,220
0,250
0,000
0,310
0,220
0,110
72,00
–0,020
5
0,000
0,250
0,350
0,210
0,350
0,250
0,000
0,010
6
0,000
0,250
0,100
0,046
0,046
0,046
0,000
0,010
7
–0,080
0,250
–0,605
0,046
0,020
0,023
0,000
0,010
8
0,060
0,250
0,046
0,046
0,020
0,023
90,00
0,010
9
0,060
–0,625
–0,105
0,056
0,100
0,040
90,00
–0,020
10
0,000
–0,625
0,100
0,056
0,100
0,056
0,000
0,020
11
0,000
0,250
–0,100
0,046
0,046
0,046
0,000
0,010
12
0,000
0,250
–0,605
0,023
0,023
0,023
0,000
0,010
Проекционные данные. Рассмотрим случаи вариантов сканирования.
1. Охват системой сбора данных ровно 50 % углового размера объекта. Производится сканирование объекта путем его вращения из единственного центра на 360º;
2. Охват системой сбора данных несколько более 50 % углового размера объекта. Производится сканирование объекта на 360º из единственного центра вращения;
3. Охват системой сбора данных 50 % (или несколько более) углового размера объекта. Производится два сканирования объекта на 360º из различных центров вращения. При этом следует обеспечить требуемые начальные угловые положения объектов или (при определенных условиях) можно начинать вращения объекта с одинаковых угловых положений, с последующим учетом кольцевого сдвига проекций. В результате можно получить проекционные данные для полного охвата. Как ранее нами было показано [5], для начала выполнения операций свертки нет необходимости в получении полных проекций (100 %). Свертка может выполняться синхронно с получением проекционных данных при частичном охвате объекта конусным пучком.
Весовые функции. Проекционные данные при частичном охвате перед выполнением свертки необходимо сгладить и учесть масштабы. Так, при 50 % охвате (случай 1) центральный отсчет берется с весом k(0) = 1, все последующие (i > 0) — с весом k(i) = 2.
В случае несколько большего чем 50 % охвата (50 % + ndop — cлучай 2) предложено ввести переходную зону для 2ndop + 1 центральных детекторов с весовым коэффициентом
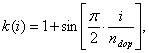
i = –ndoр…ndop. (6)
При i > ndop весовой коэффициент k(i) = 2.
Сканирование из двух центров (случай 3) не требует коррекции проекционных данных (k(i) = 1).
Ядро. В качестве ядра используется ядро Шеппа–Логана g(t) для параллельных лучей с учетом известной модификации на расхождение веерного пучка [6].
(7)
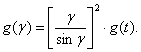
В качестве g(t) могут быть выбраны и другие ядра с соответствующими характеристиками
Свертка. Проекционные данные p(b, g, q)kor после коррекции весовой функцией k(i), а также учета положения луча в конусном пучке (g, q) имеют вид
p(b, g, q)kor = p(b, g, q)×p(b, g, q)×k(i)×cos(g)×R×(R2 + q2)–1/2, (8)
и готовы к операции свертки p(b, g, q)св с ядром g(g).
(9)
Обратное проецирование. Особенностью реализации обратного проецирования является организация самого внутреннего цикла по z. Это позволяет при адресации свернутых проекций для всех значений z использовать постоянный весовой коэффициент (3) w(x, y, b), неизменный адрес по g (x, y, b) (4), а также простое вычисление адреса в соответствии с выражением (5) q(x, y, z, b) = z*const.
Результаты моделирования. В качестве модели использовался фантом Шеппа–Логана.
Исходные параметры фантома приведены выше в таблице.
Матричная детекторная система позволяет регистрировать Ndg отсчетов в Ndz равномерно расположенных секторах с углом раствора 2gmax. Система сбора данных за одно вращение объекта позволяет собрать M проекций по Ndg*Ndz отсчетов. Результаты моделирования даются в виде матрицы размером Mt×Mt×izsl (izsl — число слоев). Моделирование проводилось при следующих численных значениях параметров:
Ndg = 101; Ndz = 101; gmax = 0,1; M = 600; Mt = 201; izsl = 81.
Для сравнения результатов реконструкции на рис. 1 показаны значения плотностей для трех взаимно ортогональных сечений исходного фантома (z = 112, y = 128, x =100), а также гистограмма плотностей по x (пересечение плоскостей z = 112; y = 150). Ниже на рис. 2–6 показаны результаты реконструкции фантома для различных условий сканирования.
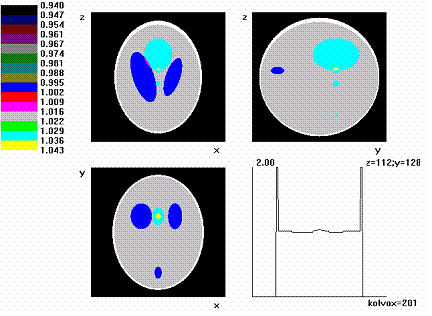
Рис. 1. Фантом Шеппа–Логана. Матрица 201×201×201.
Приведены результаты сечения фантома ортогональными плоскостями (y = 128, z = 112, x = 100)
Как видно из рисунков при сканировании с 50 % охватом получаются результаты реконструкции малоконтрастных деталей объекта довольно низкого качества (рис. 2).
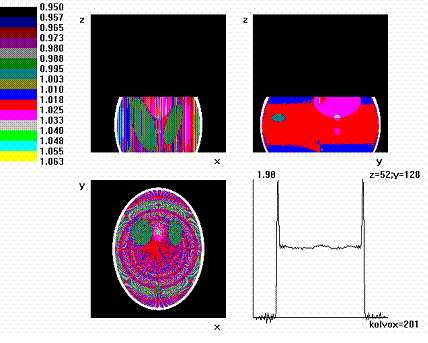
Рис. 2. Реконструкция фантома Шеппа–Логана при охвате 50 % объекта. Матрица 201×201×81. Окно 0,95–1,07. Результаты сечения фантома ортогональными плоскостями (y = 128, z = 52, x = 100)
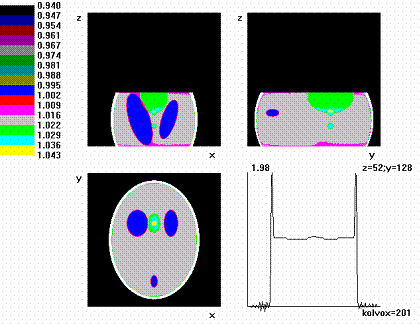
Рис. 3. Реконструкция фантома Шеппа–Логана при охвате более 50 % объекта (детекторов по дуге Ndg + ndop = 101 + 10). Матрица 201×201×81. Окно 0,94–1,05. Результаты сечения фантома
ортогональными плоскостями (y = 128, z = 52, x = 100)
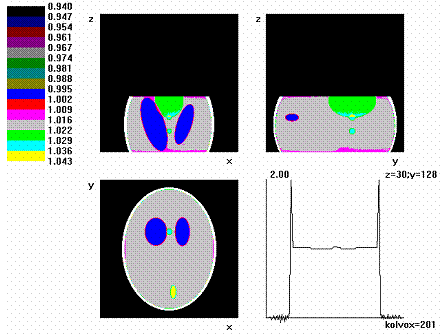
Рис. 4. Реконструкция фантома Шеппа–Логана при 100 % охвате объекта
(детекторов по дуге Ndg =101, 2 центра вращения). Матрица 201×201×81.
Окно 0,94–1,05. Сечения ортогональными плоскостями (y = 128, z = 30, x = 100)
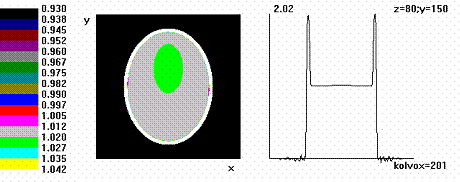
Рис. 5. Реконструкция фантома Шеппа–Логана при охвате более 50 % объекта
(детекторов по дуге Ndg + ndop = 101 + 10). Матрица 201×201×81. Окно 0,93–1,05.
Реконструкция наиболее удаленного от центра слоя z = 80
Незначительное увеличение охвата свыше 50 % существенно улучшает качество реконструкции (рис. 3, 5), позволяет ограничиться вращением объекта вокруг единственного центра сканирования. Вращение объекта вокруг двух центров целесообразно при его достаточно большой асимметрии.
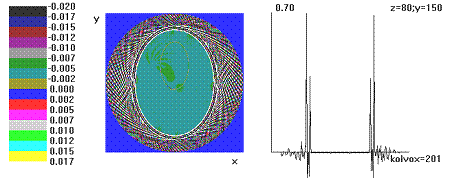
Рис. 6. Разность плотностей реконструированного и эталонного фантома Шеппа–Логана.
Охват более 50 % объекта, детекторов по дуге Ndg + ndop = 101 + 10.
Реконструкция наиболее удаленного от центра слоя z = 80. Окно –0,02…0,02
Выводы
Рассмотренные методы объемной реконструкции «больших» объектов позволяют строить сравнительно простые томографические установки промышленного назначения. Эти методы допускают частичный охват исследуемого объекта измерительной системой, что позволяет в качестве матрицы детекторов высокого разрешения использовать рентгенооптический преобразователь с цифровой видеокамерой.
1. Henrik Turbell. Cone-Beam Reconstruction Using Filtered Backprojection. — Dissertation № 000, Linkoping Studies in Science and Technology, Sweden. — 2001.
2. Hanna Andersson, Maria Magnusson Seger, Mens Mengerd. Tomography for Large Objects // SSAB-2001, Norrkoping, Sweden. — 2001.
3. TOMOHAWK CT Inspection System, NEW! Multiple Rotation Imaging —http://www. /ndt/tomohawk/tomohawk. html.
4. , Практические аспекты реализации алгоритмов объемной реконструкции контрастных объектов // Реєстрація, зберігання і оброб. даних. — 2003, — Т. 5, № 2. — C. 10–17.
5. , Избыточность проекционных данных и пути ее использования для повышения эффективности промышленных томографов // Реєстрація, зберігання і оброб. даних. — 2003. — Т. 5, № 2. — С. 85–93.
6. , , и др. Введение в современную томографию. — К.: Наук. думка, 1983. — 345 c.
Поступила в редакцию 05.09.2003





