Министерство Образования Российской Федерации
Новосибирский Государственный Технический Университет
ЛАБОРАТОРНАЯ РАБОТА ПО ДИСЦИПЛИНЕ
«Теория Игр и Исследование Операций»
Тема: многокритериальные задачи линейного и нелинейного программирования
Группа: ПМ-93
Студенты:
Преподаватель:
Новосибирск ’02
Цель работы: исследование многокритериальных задач линейного и нелинейного прог-раммирования при различных компромиссных критериях.
Задание работы:
- Определить тип компромиссного критерия, который необходимо использовать для решения варианта задания
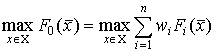 , (случай единой шкалы)
, (случай единой шкалы)
или
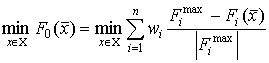 , (случай различных шкал)
, (случай различных шкал)
- Используя программное обеспечение решения задач линейного и квадратичного программирования, исследовать влияние весовых коэффициентов wi.
- Изобразить множество допустимых значений критериев в координатах Fi(Fj) в со-ответствии с вариантом задания. Найти Парето - оптимальное множество решений.
Вариант задания (6):
Критерии для задачи линейного программирования:
![]() ,
, ![]() .
.
Критерии для задачи квадратичного программирования:
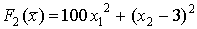 ,
, ![]()
Система ограничений (допустимое множество переменных факторов):
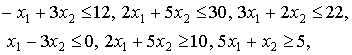
![]() .
.
Постановка многокритериальных задач для линейного и нелинейного программирования:
![]() ,
,![]()
РЕШЕНИЕ
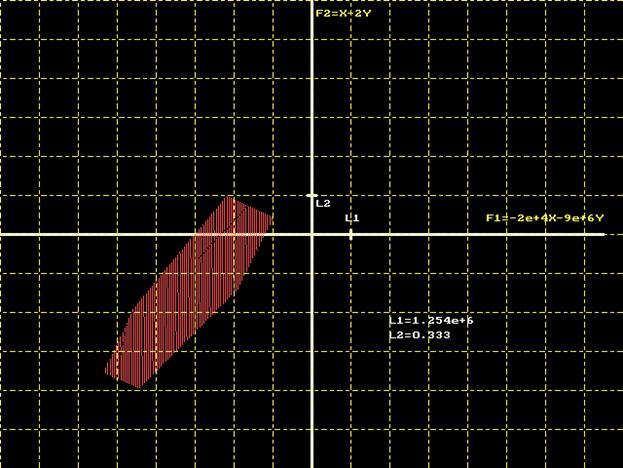
Для начала изобразим ту область на вещественной плоскости, в которой нас вынуждают локализоваться ограничения.
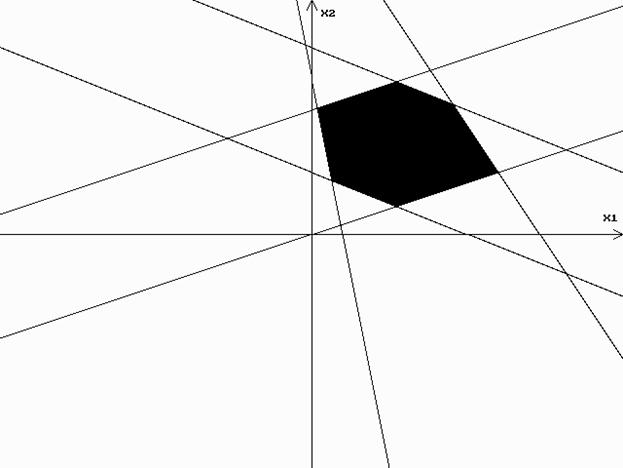
Отсюда сразу видно, что в принципе ограничение на отрицательность вектора X является излишним. Но для полноты анализа метода оставим это условие.
Мы имеем задачу принятия решения в условиях определенности при наличии двух кри-териев. Поскольку критерии сформулированы относительно максимизации некоторых абст-рактных величин, будем полагать, что оба критерия измеряются в одинаковых шкалах, а это значит, что обобщенный критерий будем выбирать в виде:
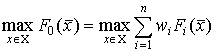 ,
,
где n=2,3, w2=1-w1.
ЛИНЕЙНЫЕ ЗАДАЧИ.
Согласно варианту задания, обобщенный критерий будет выглядеть так:
MaxF0 = Max (W1*F2+W2*F3) = Max (F3+W*(F2-F3)), W из [0,1].
![]() ,
, ![]() .
.
MaxF0 = Max (x1- 2*x2 + W*(-20001*x*x2));
На самом деле, F0 задает ничто иное как плоскость в пространстве (x1,x2,F0). Мы пом-ним, что оптимальное решение задачи линейного программирования достигается в угловой точки многогранника решений, а значит оптимальное решение будет зависеть от расположения плоскости F0 и плоскостью X1-O-X2.
Воспользуемся симплекс-методом и вычислим оптимальные компромиссные решения для различных W.
Содержимое файла VIHOD. TXT для значений W из [0,1]:
Cетка по W была подроблена с шагом 0.01;
W=0.000; Xopt=(6.000,2.000);
W=0.010; Xopt=(2.727,0.909);
W=0.020; Xopt=(2.727,0.909);
W=0.030; Xopt=(2.727,0.909);
W=0.040; Xopt=(2.727,0.909);
…………………………………………………………………………
W=1.000; Xopt=(2.727,0.909);
Выбирая шаг 1е-7, получим:
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(2.727,0.909);
W=0.; Xopt=(2.727,0.909);
W=0.; Xopt=(2.727,0.909);
W=0.; Xopt=(2.727,0.909);
………………………………………………………………………………………
W=0.; Xopt=(2.727,0.909);
Это означает, что в действительности, критерии третий и второй, измеренные в единой шкале, настолько разновесомы, что второй критерий буквально «забивает» третий при крайне незначительном отклонении параметра от 0: это обусловлено тем, что при некоторых соотно-симых w (0.4-0.6) – легко увидеть на графике, что третий критерий выглядит незначительной помехой к уравнению плоскости, задаваемой вторым критерием.
На рисунке на следующей странице зеленой точкой показана точка (6,2), а красной – точка (2,727; 0,909). Из рисунка можно увидеть, что действительно, поскольку второй критерий имеет молниеносное убывание по фактору x2, то максимум будет достигаться при плане, имеющем минимальную x2-компоненту.
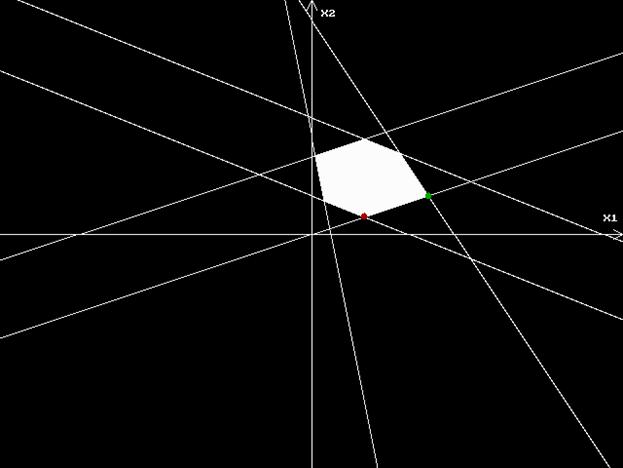
Теперь попробуем предположить, что столь различный вид критериев (величина коэффи-циентов) обусловлен разнородностью шкал этих критериев, и попробуем воспользоваться вто-рым представлением обобщенного критерия.
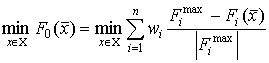
Для того, чтобы воспользоваться таким критерием, нужно найти максимальные значения на допустимом множестве X каждого из критериев, что есть однокритериальные задачи линейного программирования.
Решая эти задачи симплекс-методом, находим, что:
F2max = -8.236363e+006 (достигается в точке (2.727,0.909));
F3max = 2 (достигается в точке (6,2) – как и было показано ранее)
Тогда обобщенный критерий можно записать в виде:
MinF0 = min([(F3max-F3)/|F3max|]+ W ((F2max-F2)/|F2max|]-(F3max-F3)/|F3max|]);
В результате наблюдается следующая картина:
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
………………………………………………………………………………………
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(2.727,0.909);
W=0.; Xopt=(2.727,0.909);
W=0.; Xopt=(2.727,0.909);
……………………………………………………………………………………
W=0.; Xopt=(2.727,0.909);
W=1.; Xopt=(2.727,0.909);
Очевидна более хорошая сбалансированность критериев: теперь выбирая W на переходах между оптимальными точками, например W=0.312, мы можем быть убеждены, что оба критерия дают неплохие результаты, в то время как при ненормированном обобщенном кри-терии, требуя от третьего критерия хоть какой-нибудь весомости, мы сводили на нет второй критерий. (Эти факты следуют из непрерывности критериев, как линейных функций).
Осталось изобразить допустимое множество значений критериев в координатах F2(F3) и выделить Парето - оптимальное множество. Для этого сделаем следующим образом, возьмем квадрат [x1,x2] = [0,0; 6,6] – равномерно рассыпем в нем точек, посчитаем значения критериев и сразу оговорим, что верхняя граница этого множества должна быть Парето – оптимальным множеством, так как исходная задача была задачей максимизации критериев.
КВАДРАТИЧНЫЕ ЗАДАЧИ.
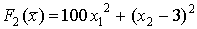 ,
, ![]()
Так выглядят критерии F2 и F3. Составим обобщенный критерий как взвешенную сумму:
MaxF0 = Max ((sqr(X1-10)+sqr(X2-10)) + W*(100sqr(X1)+sqr(X2-3)-sqr(X1-10)-sqr(X2-10)));
Будем решать задачу методом Баранкина и Дорфмана, поскольку сумма двух квадратич-ных форм представляет собой квадратичную форму, а сумма двух линейных – линейную.
Содержимое файла VIHOD. TXT для значений W из [0,1]:
Cетка по W была подроблена с шагом 0.01;
………………………………
W=0.; Xopt=(0.652,1.739);
W=0.; Xopt=(0.652,1.739);
W=0.; Xopt=(0.652,1.739);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
W=0.; Xopt=(6.000,2.000);
…………………………………………………………………………………
W=0.; Xopt=(6.000,2.000);
Квадратичная функция в этом случае, как было видно принимает свои оптимальные значения тоже в угловых точках допустимой области.
Не будем останавливаться на минимизации суммы нормированных критериев, пос-кольку шкалы обоих критериев идентичны.
Изобразим Парето – оптимальное множество решений – часть границы области допустимых критериев: