математическАЯ статистикА
Математическая статистика - это наука, занимающаяся методами обработки результатов опытов или наблюдений над случайными явлениями.
Хотя аппарат математической статистики связан со случайными явлениями, но в отличие от теории вероятностей методы математической статистики позволяют охарактеризовать случайное явление по его ограниченной выборке.
Имея статистический материал n измерений какой-либо случайной величины (выборку), необходимо решить следующие основные задачи:
1) представить статистический материал в наиболее удобном виде;
2) оценить неизвестные характеристики исследуемой случайной величины;
3) проверить статистические гипотезы о параметрах или природе анализируемой модели.
Таким образом, математическая статистика помогает исследователю лучше разобраться в опытных данных, полученных в результате наблюдений над случайными явлениями: оценить значимы или не значимы наблюдаемые факты; принять или отбросить те или иные гипотезы о природе явления.
Вместе с тем методы математической статистики широко применяются для обработки статистических данных, не имеющих вероятностной природы, поэтому они широко применяются во многих областях человеческой деятельности: политике, экономике, финансах, медицине, военном деле и др.
10. Основные понятия математической статистики и статистическое распределение выборки
Результат n независимых измерений случайной величины X представляет собой выборку (x1, x2, ... , xn) из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением ввероятностей величины Х. Последняя называется распределением генеральной совокупности, а его параметры - параметрами генеральной совокупности. В большинстве приложений теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка. Если эксперимент охватывает генеральную совокупность объектов, то полученный набор экспериментальных данных назывется генеральной выборкой.
Первое, что попадает в руки аналитика - это протокол в котором зарегистрированы: номер опыта i и значение хi, которое приняла в этом опыте случайная величина Х. Такой протокол, представленный в виде таблицы или виде вектора, называют первичной статистической совокупностью. При большом числе опытов n рассмотрение и осмысливание таблиц или векторов первичной статистической совокупности затруднительно, поэтому производят ее упорядочение. Например, размещают результаты опыта в порядке возрастания случайной величины. Таким образом получают упорядоченную статистическую совокупность. Размах выборки есть разность между наибольшим и наименьшим значением хi.
По упорядоченной статистической совокупности уже можно построить статистическую функцию распределения:
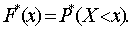
Функция ![]() - разрывная ступенчатая функция, равная нулю левее наименьшего наблюденного значения случайной величины Х и единице, правее наибольшего. Теоретически она должна иметь n скачков, где n - число опытов (размер выборки), а величина каждого скачка должна быть равной
- разрывная ступенчатая функция, равная нулю левее наименьшего наблюденного значения случайной величины Х и единице, правее наибольшего. Теоретически она должна иметь n скачков, где n - число опытов (размер выборки), а величина каждого скачка должна быть равной ![]() - частоте наблюдаемого значения случайной величины n. Практически, если одно и то же значение наблюдалось несколько раз, соответствующие скачки сливаются в один, так что общее число скачков равно числу различных наблюденных значений случайной величины. Величина скачка в каждой точке
- частоте наблюдаемого значения случайной величины n. Практически, если одно и то же значение наблюдалось несколько раз, соответствующие скачки сливаются в один, так что общее число скачков равно числу различных наблюденных значений случайной величины. Величина скачка в каждой точке ![]() равна
равна ![]() , где
, где ![]() - число повторений значения
- число повторений значения ![]() в полученной выборке.
в полученной выборке.
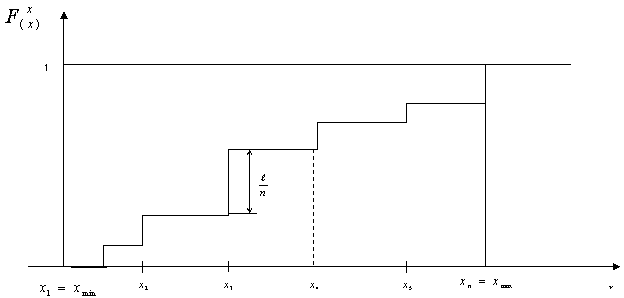
Рис. 1
Очевидно, что другие n опытов дали бы несколько иной график функции ![]() , но общая тенденция сохранилась бы. При неограниченном увеличении n кривая
, но общая тенденция сохранилась бы. При неограниченном увеличении n кривая ![]() будет приближаться (сходиться по вероятности) к функции распределения
будет приближаться (сходиться по вероятности) к функции распределения ![]() cлучайной величины Х. На практике применяются другие, более простые способы построения законов распределения случайной величины по опытным данным.
cлучайной величины Х. На практике применяются другие, более простые способы построения законов распределения случайной величины по опытным данным.
Для того, чтобы составить себе общее представление о законе распределения случайной величины X, незачем фиксировать каждое наблюденное значение и строить статистическую функцию распределения. Этим целям лучше служат группированный статистический ряд и гистограмма.
Для построения группированного статистического ряда весь участок оси абсцисс, на котором расположены значения случайной величины X, наблюдавшиеся в опыте, делятся на участки или “разряды”. Длины разрядов необязательно брать равными друг другу: бывают случаи, когда на участках оси абсцисс, где наблюденные значения X располагаются гуще, удобнее брать разряды более мелкими, а там где реже - более крупными (или объединять два или более равных по длине разрядов в один). Границы разрядов удобно брать “круглыми” числами.
Группированным статистическим рядом называется таблица, где в верхней строке указаны разряды: от и до, в нижней - соответствующие им частоты:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
причем 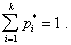
Частота ![]() события
события 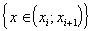 вычисляется как отношение числа
вычисляется как отношение числа ![]() опытов, в которых случайная величина
опытов, в которых случайная величина ![]() попала в
попала в ![]() -й разряд
-й разряд ![]() к общему числу
к общему числу ![]() проведенных опытов:
проведенных опытов:
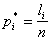 .
.
Если значение случайной величины попало в точности на границу между разрядами, то её можно отнести либо к левому разряду, либо к правому (ведь вероятность того, что непрерывная случайная величина ![]() примет заранее заданное значение, равна нулю). Можно использовать и “симметричное правило”: если значение случайной величины попало в точности на границу разрядов, то разделить его поровну между соседними разрядами и прибавить по
примет заранее заданное значение, равна нулю). Можно использовать и “симметричное правило”: если значение случайной величины попало в точности на границу разрядов, то разделить его поровну между соседними разрядами и прибавить по ![]() к числам
к числам ![]() для обоих разрядов.
для обоих разрядов.
Число разрядов, на которые следует группировать статистические данные, не должно быть слишком большим ( тогда ряд распределения становится слишком невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны оно не должно быть слишком малым (при этом свойства распределения описываются слишком грубо). Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка ![]() .
.
Группированный статистический ряд часто оформляется графически в виде так называемой гистограммы - статистического аналога кривой распределения. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды и на каждом разряде как его основание строится прямоугольник, площадь которого равна частоте данного разряда (высота прямоугольника равна частоте данного разряда ![]() , разделенной на его длину
, разделенной на его длину ![]() ). Из способа построения гистограммы следует, что полная площадь ее равна единице.
). Из способа построения гистограммы следует, что полная площадь ее равна единице.
Очевидно, что при увеличении числа опытов можно выбирать все более и более мелкие разряды, при этом гистограмма будет все более приближаться к некоторой кривой ограничивающей площадь, равную единице.
Эта кривая представляет собой график статистической плотности распределения ![]() величины Х.
величины Х.
Имея в своем распоряжении группированный статистический ряд, можно приближенно построить и статистическую функцию распределения ![]() величины Х.
величины Х.
В качестве тех значений х, для которых вычисляется ![]() , естественно, взять границы разрядов. Тогда, очевидно:
, естественно, взять границы разрядов. Тогда, очевидно:
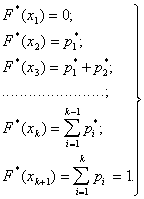
Соединяя полученные точки плавной кривой, получим приближенный график статистической функции распределения.
Пример. Измерено n=100 сопротивлений определенного вида. В таблице приведены номер опыта i и соответствующие значения сопротивления ![]() (в омах).
(в омах).
i
xi
i
xi
i
xi
i
xi
i
xi
1
87
21
82
41
88
61
108
81
84
2
85
22
111
42
90
62
95
82
105
3
91
23
115
43
101
63
99
83
110
4
102
24
99
44
95
64
92
84
102
5
80
25
96
45
93
65
100
85
104
6
75
26
101
46
32
66
118
86
107
7
94
27
115
47
88
67
103
87
120
8
102
28
100
48
94
68
102
88
108
9
99
29
97
49
98
69
89
89
107
10
101
30
91
50
99
70
90
90
98
11
100
31
87
51
102
71
94
91
96
12
120
32
116
52
101
72
106
92
106
13
122
33
121
53
122
73
112
93
110
14
101
34
101
54
99
74
122
94
115
15
88
35
123
55
97
75
100
95
95
16
80
36
97
56
95
76
92
96
109
17
97
37
95
57
105
77
83
97
111
18
92
38
88
58
112
78
82
98
103
19
91
39
104
59
116
79
111
99
88
20
94
40
111
60
118
80
102
100
108
Имея первичную статистическую совокупность, получить упорядоченную статистическую совокупность; построить группированный статистический ряд с шестью равномерными разрядами; гистограмму и статистическую функцию распределения.
Решение: Упорядоченная статистическая совокупность имеет вид:
i
xi
i
xi
i
xi
i
xi
i
xi
1
75
21
92
41
97
61
102
81
111
2
80
22
92
42
98
62
102
82
111
3
80
23
92
43
98
63
102
83
111
4
82
24
92
44
99
64
102
84
111
5
82
25
93
45
99
65
103
85
112
6
84
26
93
46
99
66
103
86
112
7
85
27
94
47
99
67
104
87
115
8
87
28
94
48
99
68
104
88
115
9
87
29
94
49
100
69
105
89
115
10
88
30
95
50
100
70
105
90
116
11
88
31
95
51
100
71
106
91
116
12
88
32
95
52
100
72
106
92
118
13
88
33
95
53
101
73
107
93
118
14
88
34
95
54
101
74
107
94
120
15
89
35
95
55
101
75
108
95
120
16
90
36
96
56
101
76
108
96
121
17
90
37
96
57
101
77
108
97
122
18
91
38
97
58
101
78
109
98
122
19
91
39
97
59
102
79
110
99
122
20
91
40
97
60
102
80
110
100
123
Если в таблице первичной статистической совокупности одно и то же значение встречается несколько раз, то и в таблице упорядоченной статистической совокупности его надо писать столько же раз.
Для группированного статистического ряда выберем “круглые” границы разрядов: (70-80); (80-90); (90-100); (100-110); (110-120); (120-130).
Подсчитывая количество значений случайной величины, попавших в каждый разряд (считая половинки от попавших в границу между разрядами) и деля это значение на число опытов n=100, получим группированный статистический ряд:
Разряды
70:80
80:90
90:100
Частоты
0,02
0,14
0,34
Разряды
100:110
110:120
120:130
Частоты
0,29
0,15
0,06
Откладывая по оси абсцисс разряды и строя на каждом разряде как на основании прямоугольник с площадью ![]() , получим гистограмму (рис. 2).
, получим гистограмму (рис. 2).
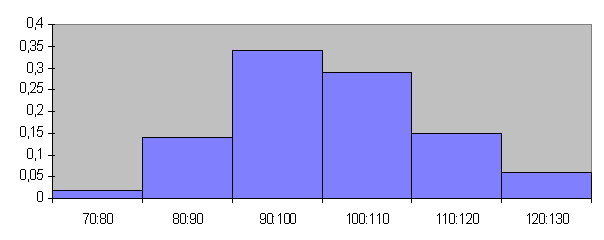
Рис. 2
Пользуясь группированным статистическим рядом, находим:
F*(70) = 0; F*(80) = 0,02; F*(90) = 0,02 + 0,14 = 0,16;
F*(100) = 0,02 + 0,14 + 0,34 = 0,5; F*(110) = 0,5 + 0,29 = 0,79;
F*(120) = 0,79 + 0,15 = 0,94; F*(130) = 0,94 + 0,06 = 1.
График статистической функции распределения показан на рис. 3.
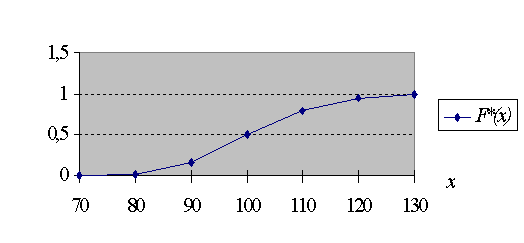
Рис. 3
Для нахождения законов распределения случайной величины по результатам опытов нужно располагать достаточно обширным статистическим материалом, порядка нескольких сотен опытов (наблюдений). Однако на практике нередко приходится иметь дело со статистическим материалом весьма ограниченного объема - с двумя-тремя десятками наблюдений, часто даже меньше. Такого ограниченного материала недостаточно, чтобы найти заранее неизвестный закон распределения случайной величины, но все же он может быть использован для оценок важнейших числовых характеристик случайной величины: математического ожидания, дисперсии, иногда - высших моментов.
На практике нередко бывает что вид закона распределения заранее известен, а требуется найти только параметры, от которых он зависит (например m и ![]() для Гауссового закона). Наконец в некоторых задачах закон распределения случайной величины вообще несущественен, а требуется знать только ее числовые характеристики.
для Гауссового закона). Наконец в некоторых задачах закон распределения случайной величины вообще несущественен, а требуется знать только ее числовые характеристики.
Выводы
1. Математическая статистика - это наука, занимающаяся методами обработки результатов опытов или наблюдений над случайными явлениями. Вместе с тем математический аппарат математической статистики используется для различных задач прикладной статистики, в которых необязательны допущения о вероятностной природе обрабатываемых данных.
2. Математическая статистика решает три основные задачи:
- представление статистического материала в наиболее удобном для анализа виде;
- оценка неизвестных характеристик исследуемой случайной величины по ее ограниченной выборке;
- проверка статистических гипотез о параметрах и законах распределения случайных величин.
3. Основными понятиями математической статистики являются: выборка, первичная статистическая совокупность, упорядоченная статистическая совокупность, группированный статистический ряд, гистограмма, а также статистические характеристики результатов опыта - аналоги характеристик случайной величины, определенные в теории вероятностей.
11. Статистические оценки параметров распределения
Численные значения (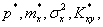 ....) характеристик (
....) характеристик (![]() ....) случайных величин, получаемых в результате обработки результатов эксперимента (опыта), называются оценками указанных характеристик.
....) случайных величин, получаемых в результате обработки результатов эксперимента (опыта), называются оценками указанных характеристик.
Так как результат эксперимента случаен, то и любая оценка является случайной величиной. Чтобы случайная оценка ![]() наилучшим образом оценивала исходную характеристику
наилучшим образом оценивала исходную характеристику ![]() случайной величины, она должна быть несмещенной, состоятельной и эффективной.
случайной величины, она должна быть несмещенной, состоятельной и эффективной.
Несмещенной называется такая оценка ![]() , математическое ожидание которой равно оцениваемой характеристике
, математическое ожидание которой равно оцениваемой характеристике ![]() :
:
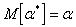 .
.
Состоятельной называется такая оценка ![]() , которая при увеличении числа опытов (объема выборки) n приближаеться (сходится по вероятности) к исходному значению
, которая при увеличении числа опытов (объема выборки) n приближаеться (сходится по вероятности) к исходному значению ![]() :
:
![]() .
.
Эффективной называется такая несмещенная оценка ![]() , которая обладает по сравнению с другими минимальной дисперсией:
, которая обладает по сравнению с другими минимальной дисперсией:
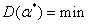 .
.
На практике не всегда удается удовлетворить всем этим требованиям. Например, иногда формулы для вычисления эффективной оценки очень сложны, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше.
Естественной оценкой для математического ожидания ![]() случайной величины Х является среднее арифметическое элементов выборки (статистическое среднее):
случайной величины Х является среднее арифметическое элементов выборки (статистическое среднее):
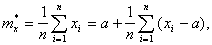
где ![]() - новое начало отсчета, вводимое для удобства расчетов.
- новое начало отсчета, вводимое для удобства расчетов.
Можно показать, что эта оценка является несмещенной, состоятельной, а для гауссового закона распределения и эффективной.
В случае неравноточных измерений оценкой математического ожидания ![]() случайной величины
случайной величины ![]() служит средневзвешенное результатов n опытов:
служит средневзвешенное результатов n опытов:
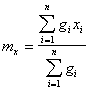 ,
,
где ![]() - числа, обратнопропорциональные квадратам среднеквадратичных отклонений
- числа, обратнопропорциональные квадратам среднеквадратичных отклонений ![]() -го опыта (gi =
-го опыта (gi = ![]() , i= 1, 2,....., n)
, i= 1, 2,....., n)
Несмещенная оценка дисперсии при неизвестном математическом ожидании:
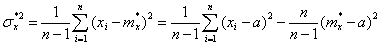 .
.
Иногда удобно использовать выражение для оценки дисперсии следующего вида:
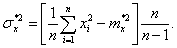
При большом значении n поправочный множитель ![]() становится близким к единице и его применение теряет смысл.
становится близким к единице и его применение теряет смысл.
Несмещенная, состоятельная оценка корреляционного момента случайных величин имеет вид:
![]()
Корреляционный момент можно вычислить и по равносильной формуле:
![]()
Оценка коэффициент корреляции:
![]()
При известных математических ожиданиях ![]() оценками дисперсии и корреляционного момента являются:
оценками дисперсии и корреляционного момента являются:
![]()
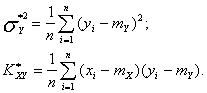
Пример. Произведено 10 фиксаций курса валюты Х и валюты У. Результаты (в условных единицах) сведены в таблицу:
i
1
2
3
4
5
6
7
8
9
10
xi
1.8
1.85
1.85
1.7
1.72
1.77
1.8
1.83
1.89
1.89
yi
1.5
1.5
1.45
1.5
1.6
1.6
1.55
1.5
1.55
1.55
Найти оценки для числовых характеристик системы случайных величин (Х, У).
Решение:
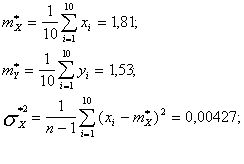
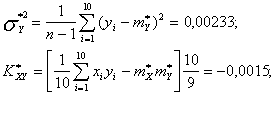
![]()
Мы видим, что между курсами валют Х и У существует корреляционная связь (причем отрицательная: при увеличении курса одной валюты уменьшает и курс другой).
Часто на практике возникает задача не только определения оценок числовых характеристик случайных величин по их ограниченной выборке но и ориентировочная оценка их точности и надежности. Нас интересует, с какой вероятностью можно утверждать, что допущенная при оценке ошибка не превзойдет некоторой величины ![]() ? Обозначим эту вероятность
? Обозначим эту вероятность ![]()
![]()
Вероятность ![]() называется доверительной вероятностью;
называется доверительной вероятностью;
границы ![]() - доверительными границами;
- доверительными границами;
интервал ![]() - доверительным интервалом.
- доверительным интервалом.
Вероятность ![]() характеризует надежность оценки, а величина
характеризует надежность оценки, а величина ![]() - ее точность.
- ее точность.
Может быть поставлена и другая задача, а именно: каков должен быть доверительный интервал, для того, чтобы с заданной вероятностью ![]() можно было утверждать, что истинное значение искомой характеристики не выйдет за пределы этого интервала?
можно было утверждать, что истинное значение искомой характеристики не выйдет за пределы этого интервала?
Чтобы оценить точность и надежность оценки, нужно знать ее закон распределения. Согласно центральной предельной теоремы теории вероятностей, он во многих случаях оказывается близким к гауссовому.
Допуская, что оценка математического ожидания ![]() есть случайная величина с гауссовым распределением и с параметрами
есть случайная величина с гауссовым распределением и с параметрами ![]() находим приближенно вероятность того, что оценка
находим приближенно вероятность того, что оценка ![]() отклоняются от своего математического ожидания меньше, чем на
отклоняются от своего математического ожидания меньше, чем на ![]() :
:
![]()
где Ф(х) - функция Лапласа.
Пример. При обработке результатов n=20 независимых опытов получены оценки 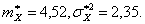 Найти вероятность того, что, полагая
Найти вероятность того, что, полагая ![]() мы не совершим ошибки, большей, чем
мы не совершим ошибки, большей, чем ![]()
Решение: Находим ![]()
Тогда ![]()
Итак, вероятность того, что ошибка от замены ![]() на
на ![]() не превзойдет 0,3, не настолько велика, чтобы считать это событие практически достоверным.
не превзойдет 0,3, не настолько велика, чтобы считать это событие практически достоверным.
Если задана доверительная вероятность ![]() (на практике ее берут от 0,8 до 0,999), то из уравнения
(на практике ее берут от 0,8 до 0,999), то из уравнения
![]()
находим ![]()
где значение t![]() удовлетворяет равенству
удовлетворяет равенству ![]()
Пример. Произведено 16 измерений случайной величины Х. Вычисленные по результатам измерений оценки характеристик случайной величины Х следующие:
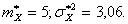
Определить доверительный интервал для математического ожидания с надежностью 0,9.
Решение: Из таблицы функции Лапласа, определяем, что если 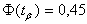 , то
, то 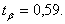
Тогда ![]()
Таким образом, интервал ![]() накрывает точку
накрывает точку ![]() с вероятностью 0,9.
с вероятностью 0,9.
Для дисперсии гауссовой случайной величины Х приближенное значение ![]() может быть вычислено по формуле:
может быть вычислено по формуле:
![]()
а для корреляционного момента:
![]()
Приведенные формулы для определения доверительного интервала дают хорошие результаты для оценки математического ожидания при 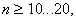 а для дисперсии и корреляционного момента - при n>20...30.
а для дисперсии и корреляционного момента - при n>20...30.
При меньшем числе опытов результаты получаются приближенными.
В заключение приведем оценку вероятности события. Пусть произведено n независимых опытов, в которых событие А появилось m раз. Требуется оценить вероятность этого события p. Несмещенной и состоятельной оценкой вероятности события является его частота
![]()
Вероятность того, что ошибка оценки вероятности события не превысит ![]()
![]()
где 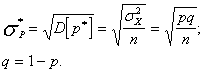
В большинстве практических задач вероятность p заранее неизвестна, поэтому ее заменяют приближенным значением ![]() . Тогда получаем приближенную формулу для определения доверительной вероятности:
. Тогда получаем приближенную формулу для определения доверительной вероятности:
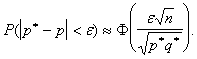
Необходимое число опытов для получения оценки вероятности события с доверительной вероятностью ![]() и доверительным интервалом определяется из формулы:
и доверительным интервалом определяется из формулы:
![]()
где ![]() определяется исходя из равенства
определяется исходя из равенства ![]() частота событий в первой серии опытов;
частота событий в первой серии опытов; ![]()
Здесь, как видим, вместо ![]() используется
используется ![]() Это обусловлено тем, что вопрос о необходимом числе опытов поставлен до их проведения.
Это обусловлено тем, что вопрос о необходимом числе опытов поставлен до их проведения.
Пример. При 600 бросаниях монеты герб выпал 312 раз. Найти вероятность того, что ошибка от замены вероятности частотой не превысит ![]()
Решение: Оценка вероятности ![]()
Тогда ![]()
Искомая вероятность ![]()
Итак, с довольно высокой вероятностью 0,986 можно утверждать, что при n=600 бросаниях монеты ошибка от замены вероятности частотой не превысит 0,05.
Выводы
1. Одна из центральных задач математической статистики заключается в вычислении на основе имеющихся статистических данных (ограниченной выборки) как можно более точных приближенных значений (статистических оценок) одной или нескольких числовых характеристик исследуемой случайной величины.
Принципиальная возможность получения работоспособных приближений такого рода на основании статистического обследования лишь части анализируемой генеральной совокупности (т. е. на основании ограниченного ряда наблюдений, или выборки) обеспечивается замечательным свойством статистической устойчивости оценок числовых характеристик.
2. Свойство состоятельности оценки обеспечивает ее статистическую устойчивость, т. е. сходимость (по вероятности) к истинному значению оцениваемого параметра по мере роста объема выборки, на основании которой эта оценка строится. Свойство несмещенности оценки заключается в том, что результат усреднения всевозможных значений этой оценки, полученных по различным выборкам заданного объема, даст в точности истинное значение оцениваемого параметра.
3. С учетом случайной природы каждого конкретного оценочного значения числовой характеристики случайной величины представляет интерес определения доверительных интервалов, которые с наперед заданной (и близкой к единице) вероятностью накрывали бы истинное значение оцениваемого параметра.
Обработка результатов наблюдений по методу наименьших квадратов
Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число опытов ограничено. Только при очень большом числе опытов эти случайности сглаживаются, и явление обнаруживает в полной мере присущие ему закономерности.
Случаен ступенчатый вид статистической функции распределения непрерывной случайной величины; случайна форма гистограммы, ограниченной тоже ступенчатой линией. Поэтому на практике часто приходится решать вопрос о том, как подобрать для данного статистического распределения аналитическую формулу, выражающую лишь существенные черты статистического материала. Такая задача называется задачей выравнивания статистических распределений.
Обычно выравниванию подвергаются гистограммы. Задача сводится к тому, чтобы заменить гистограмму плавной кривой, имеющей достаточно простое аналитическое выражение, и в дальнейшем пользоваться ею в качестве плотности распределения ![]() (рис.4).
(рис.4).
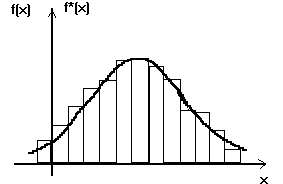
Рис. 4
Для нахождения оценок параметров функциональной зависимости применяется метод наименьших квадратов. При этом метод наименьших квадратов не решает вопроса вида аналитической функции, а дает возможность при заданном типе аналитической функции y=f(x) подобрать наиболее вероятные значения для параметров этой функции. Например, если несколько полученных в опыте точек на плоскости, ход расположены приблизительно прямой (рис.5),
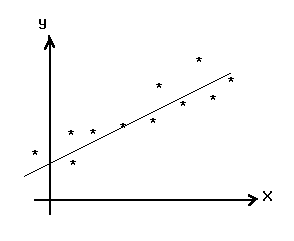
Рис. 5
то естественно возникает идея заменить эту зависимость линейной функцией y=kx+a, для которой требуется определить лишь параметры а и k. Если зависимость явно нелинейная (рис.6), в качестве аппроксимирующей кривой выбирают многочлен ![]() (в частном случае, параболу).
(в частном случае, параболу).
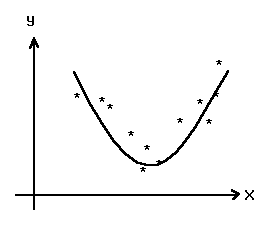
Рис. 6
При этом необходимо иметь в виду, что если производится выравнивание гистограмм, то соответствующая функция должна обладать основными свойствами плотности:
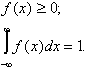
Сущность метода наименьших квадратов заключается в следующем. Пусть зависимость у от х выражается формулой
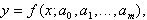
где 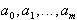 - подлежащие определению параметры.
- подлежащие определению параметры.
В результате n независимых опытов были получены следующие данные, оформленные в виде статистической таблицы:
Номер опыта
1
2
...
k
...
n
xi
x1
x2
...
xk
...
xn
yi
y1
y2
...
yk
...
yn
Согласно методу наименьших квадратов, наивероятнейшие значения параметров ![]() дают минимум функции
дают минимум функции
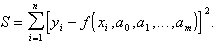
Если 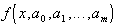 имеет непрерывные частные производные по всем неизвестным параметрам
имеет непрерывные частные производные по всем неизвестным параметрам 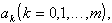 то необходимое условие минимума функции S представляет систему уравнений с m+1 неизвестными:
то необходимое условие минимума функции S представляет систему уравнений с m+1 неизвестными:
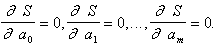
Если в качестве аппроксимирующей функции взят многочлен, т. е.
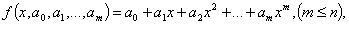
то оценка его коэффициентов 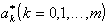 определяются из системы m+1 линейных уравнений:
определяются из системы m+1 линейных уравнений:
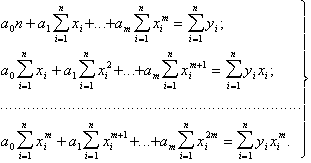
Если значения хi известны без ошибок, а значения yi независимы и равноточны, то оценка дисперсии величины yi определяется формулой
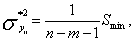
где ![]() - значение, вычисленное в предположении, что коэффициенты поли....... заменены их полученными оценками.
- значение, вычисленное в предположении, что коэффициенты поли....... заменены их полученными оценками.
При гауссовом законе распределения величин yi изложенный метод дает минимальную ошибку.
Пример 1. Найти оценки параметров линейной функции
![]()
Решение. Для определения коэффициентов ![]() и
и ![]() методом наименьших квадратов составляем систему
методом наименьших квадратов составляем систему
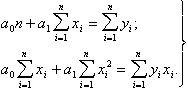
Решая систему получаем
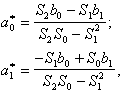
где
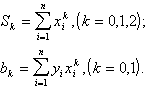
Пример 2. С помощью прибора измеряется какой-то параметр ![]() . Случайная величина Х - ошибка измерения параметра
. Случайная величина Х - ошибка измерения параметра ![]() . С целью исследования точности прибора произведено n=500 измерений этой ошибки. Результаты измерений сведены в группированный статистический ряд:
. С целью исследования точности прибора произведено n=500 измерений этой ошибки. Результаты измерений сведены в группированный статистический ряд:
Разряды
-4![]() -3
-3
-3![]() -2
-2
-2![]() -1
-1
-1![]() 0
0
0![]() 1
1
1![]() 2
2
2![]() 3
3
3![]() 4
4
Частоты ![]()
0,012
0,05
0,144
0,266
0,240
0,176
0,092
0,20
Число попаданий в i-й разряд ![]()
6
25
72
133
120
88
46
10
Определить аналитический вид плотности распределения f(x).
Решение. Вначале построим гистограмму распределения случайной величины Х.
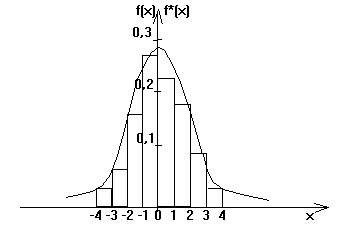
Как видно из гистограммы, подходящей для аппроксимации является гауссова функция:
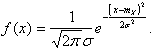
Таким образом, необходимо определить лишь два параметра, математическое ожидание ![]() и дисперсию
и дисперсию ![]() . Поскольку мы не располагаем всеми наблюденными n=500 значениями случайной величины, оценим
. Поскольку мы не располагаем всеми наблюденными n=500 значениями случайной величины, оценим ![]() и
и ![]() по группированному статистическому ряду. Делается это так: выбирается в качестве "представителя" i-го разряда его середина и этому значению хi приписывается частота
по группированному статистическому ряду. Делается это так: выбирается в качестве "представителя" i-го разряда его середина и этому значению хi приписывается частота ![]() .
.
Тогда
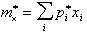 =-3,5*0,012-2,5*0,05-1,5*0,144-0,5*0,266+0,5*0,240+1,5*0,176+2,5*
=-3,5*0,012-2,5*0,05-1,5*0,144-0,5*0,266+0,5*0,240+1,5*0,176+2,5*
*0,092+3,5*0,02=0,162.
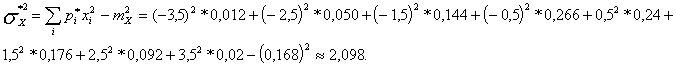
Среднее квадратическое отклонение
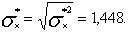
Таким образом оценку для плотности распределения случайной величины Х можно записать в виде
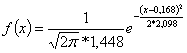 .
.
Для решения задач обоснованного прогноза, т. е. для определения пределов, в которых с наперед заданной надежностью будет содержаться интересующая нас величина, если другие связанные с ней величины получат определенные значения, необходимо определить их функциональную зависимость. Функция представляющая собой статистическую зависимость одной случайной величины от другой называется регрессией.
Для гауссового распределения системы случайных величин (X, Y) связь между ними выражается уравнениями линейной регрессии:
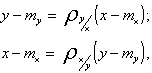
где ![]() и
и ![]() - коэффициенты линейной регрессии y на х и х на y, соответственно.
- коэффициенты линейной регрессии y на х и х на y, соответственно.
Коэффициенты линейной регрессии выражаются через характеристики системы (X, Y) следующим образом:
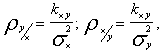
или, учитывая, что коэффициент корреляции ![]() имеем:
имеем:
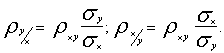
Перемножив левые и правые части этих равенств, после извлечения корня получаем
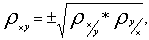
т. е. коэффициент корреляции есть среднее геометрическое коэффициентов линейной регрессии. Он характеризует насколько близко связь между случайными величинами Х и Y к линейной зависимости.
Выборочные уравнения прямых регрессий имеют вид:
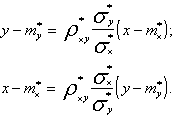
В тех случаях, когда линейное приближение является явно недостаточным, можно рассматривать в качестве приближенных уравнений регрессий более сложные функции, неизвестные параметры которой определяются методом наименьших квадратов.
Пример. Определить выборочное уравнение линейной регрессии Х по Y, если по результатам опытов получены следующие оценки:
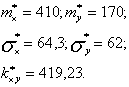
Решение. Выборочный коэффициент корреляции
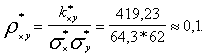
Тогда x-410=0,1*(64,3/62)*(y-170), или x=0,104y+392,32.
Выводы
1. Одной из часто встречающихся задач, встающих перед аналитиками различных специальностей, является задача нахождения зависимости между некоторыми наборами данных эксперимента. В общей постановке задача описания эмпирической зависимости с помощью параметрической регрессии предполагает, что задается функция, определенная с точностью до нескольких параметров, которые подбирают таким образом, чтобы получающаяся функция с максимальной точностью соответствовала данным эксперимента. Наиболее просто определяются параметры для случая линейной регрессии.
2. При выравнивании (сглаживании) эмпирических зависимостей наиболее часто исходят из того, что наилучшим приближением в данном классе функций является то, для которого сумма квадратов отклонений обращается в минимум. Вопрос о том, в каком классе функций следует искать наилучшее приближение, решается уже не математически, а исходя из характера эмпирической кривой. Аналогично обстоит дело и с задачей выравнивания статистических распределений. Принципиальный вид выравнивающей плавной кривой ![]() выбирается заранее, исходя из условий возникновения случайной величины Х или просто из соображений, связанных с внешним видом гистограммы.
выбирается заранее, исходя из условий возникновения случайной величины Х или просто из соображений, связанных с внешним видом гистограммы.
3. Одним из основных методов определения статистических оценок параметров, входящих в выравнивающую функцию, является метод наименьших квадратов.
12. Статистическая проверка гипотез
При решении многих задач приходится делать предположение о виде законов распределения рассматриваемых случайных величин или соотношении между их числовыми характеристиками. Такие предположения принято называть гипотезами. Приняв ту или иную гипотезу, из нее выводят определенное следствие и рассматривают, насколько оно оправдывается на опыте, т. е. проверяют согласие принятой гипотезы с опытом.
Процедура обоснованного сопоставления высказанной гипотезы с имеющимися выборочными данными осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез.
Результат подобного сопоставления может быть либо отрицательными (данные наблюдения противоречат высказанной гипотезе, а потому от этой гипотезы следует отказаться), либо неотрицательными (данные наблюдения не противоречат высказанной гипотезе, а потому ее можно принять в качестве одного из естественных и допустимых решений). При этом неотрицательный результат статистической проверки гипотезы не означает, что высказанное нами предположительное утверждение является наилучшим, единственно подходящим: просто оно не противоречит имеющимся у нас выборочным данным, однако таким же свойством могут наряду с данной гипотезой обладать и другие гипотезы.
По своему прикладному содержанию высказываемые в ходе статистической обработки данных гипотезы можно подразделить на несколько основных типов:
1. Гипотезы о типе законов распределения исследуемой величины.
2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристиках анализируемых совокупностей.
3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
Для проверки гипотезы о виде закона распределения случайной величины часто применяется критерий согласия ![]() (критерий Пирсона). Он позволяет производить проверку гипотезы соответствия опытного закона распределения теоретическому (предполагаемому) не только в случаях, когда последний известен полностью, но и тогда, когда параметры предполагаемого закона распределения определяются на основании опытных данных.
(критерий Пирсона). Он позволяет производить проверку гипотезы соответствия опытного закона распределения теоретическому (предполагаемому) не только в случаях, когда последний известен полностью, но и тогда, когда параметры предполагаемого закона распределения определяются на основании опытных данных.
Пусть проведено n независимых опытов, в каждом из которых случайная величина Х приняла определенное значение. Результаты опытов сведены в m разрядов и в виде группированного статистического ряда:
i
![]()
![]()
...
![]()
![]()
![]()
![]()
...
![]()
![]()
![]()
![]()
...
![]()
Мы выводим гипотезу Н, состоящую в том, что случайная величина Х имеет ряд распределения с вероятностями pi, i=1,2,...,m, а отклонения частот ![]() от вероятностей pi объясняются случайными причинами.
от вероятностей pi объясняются случайными причинами.
Чтобы проверить правдоподобность этой гипотезы, надо выбрать какую-то меру расхождения статистического распределения с гипотетическим.
В качестве меры расхождения R между гипотетическим распределением и статистическим при использовании критерия ![]() берется сумма квадратов отклонений
берется сумма квадратов отклонений ![]() с некоторыми весами
с некоторыми весами ![]() :
:
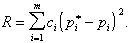
Коэффициенты ci вводятся потому, что отклонения, относящиеся к разным значениям pi, нельзя считать равноправными по значимости: одно и то же по абсолютной величине отклонение ![]() может быть малозначительным, если сама вероятность pi велика, и очень заметным, если она мала. Пирсон доказал, что если взять
может быть малозначительным, если сама вероятность pi велика, и очень заметным, если она мала. Пирсон доказал, что если взять
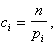
то при большом числе опытов n закон распределения величины R обладает весьма простыми свойствами: он практически не зависит от закона распределения случайной величины Х и мало зависит от числа опытов n, а зависит только от числа m значений случайной величины и при увеличении числа n приближается к распределению ![]() . При таком выборе коэффициентов сi, мера расхождения R обычно обозначается
. При таком выборе коэффициентов сi, мера расхождения R обычно обозначается ![]() :
:
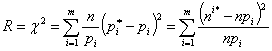
Распределение ![]() , как известно, зависит от параметра r, называемого "числом степеней свободы". При пользовании критерием
, как известно, зависит от параметра r, называемого "числом степеней свободы". При пользовании критерием ![]() число степеней свободы полагается равным числу разрядов m минус число независимых условий ("связей"), наложенных на частоты
число степеней свободы полагается равным числу разрядов m минус число независимых условий ("связей"), наложенных на частоты ![]() . Примерами таких условий могут быть:
. Примерами таких условий могут быть:
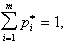
если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях); или же
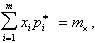
если мы требуем, чтобы совпадало статистическое среднее с гипотетическим, или же
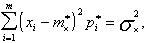
если мы требуем, кроме того, еще и совпадения дисперсий и т. д.
Для распределения ![]() составлены таблицы. Пользуясь ими, можно для каждого значения
составлены таблицы. Пользуясь ими, можно для каждого значения ![]() и число степеней свободы r найти вероятность p того, что величина, распределенная по закону
и число степеней свободы r найти вероятность p того, что величина, распределенная по закону ![]() , превзойдет это значение. Если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным.
, превзойдет это значение. Если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным.
Вопрос о том, какую вероятность p считать очень малой, чтобы отбросить или пересмотреть гипотезу, не может быть решен из математических соображений.
Обычно вероятности, не превосходящие 0,01, считают уже достаточно малыми (в других случаях считают малыми вероятности, не превосходящие 0,05). Вероятность р называют уровнем значимости критерия, а отвергающую ей область больших отклонений - критической областью.
Критерий согласия ![]() можно применять и для непрерывных случайных величин, если, приближенно заменить непрерывную случайную величину Х дискретной с возможными значениями xi*, равными середине i-го разряда, и частотами pi*, равными частоте попадания случайной величины Х в i-й разряд. Вероятности pi вычисляются по формуле
можно применять и для непрерывных случайных величин, если, приближенно заменить непрерывную случайную величину Х дискретной с возможными значениями xi*, равными середине i-го разряда, и частотами pi*, равными частоте попадания случайной величины Х в i-й разряд. Вероятности pi вычисляются по формуле
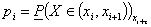 ,
,
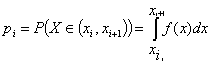 .
.
ПРИМЕР. Произведено n = 800 наблюдений над случайной величиной Х, возможные значения которой ![]()
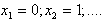 ,
,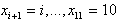 . Результаты 800 опытов представлены в виде таблицы:
. Результаты 800 опытов представлены в виде таблицы:
Xi
0
1
2
3
4
5
6
7
8
9
10
ni
25
81
124
146
175
106
80
35
16
6
6
Pi*
0,031
0,101
0,155
0,186
0,21
0,132
0,1
0,044
0,02
0,008
0,008
Требуется оценить правдоподобие гипотезы Н, состоящей в том, что Х распределена по закону Пуассона ![]() (
(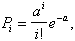 где
где ![]() =m
=m![]() ) с параметром
) с параметром ![]() , равным статистическому среднему наблюденных значений случайной величины Х. В качестве уровня значимости принять
, равным статистическому среднему наблюденных значений случайной величины Х. В качестве уровня значимости принять ![]()
Решение. Найдем статистическое среднее mx*
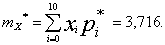
Вычислим вероятность ![]() , соответствующие закону Пуассона:
, соответствующие закону Пуассона:
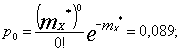
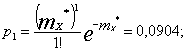
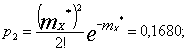 И так далее:
И так далее:
![]()
![]()
Находим значение ![]() :
:
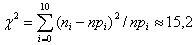
Число степеней свободы r в данном случае равно числу значений случайной величины (m=11) минус единица (первое условие ![]()
![]() ) и минус еще единица - совпадение гипотетического математического ожидания со статистическим: r=11-1-1=9. По таблице для распределения
) и минус еще единица - совпадение гипотетического математического ожидания со статистическим: r=11-1-1=9. По таблице для распределения ![]() при r=9 и
при r=9 и ![]() =15 находим р=0,1. таким образом, в данном примере гипотеза Н о пуассоновском распределении случайной величины Х противоречит опытным данным и ее надо отбросить, так как р=0,1<
=15 находим р=0,1. таким образом, в данном примере гипотеза Н о пуассоновском распределении случайной величины Х противоречит опытным данным и ее надо отбросить, так как р=0,1<![]() . Простым критерием проверки гипотезы о виде закона распределения является критерий Колмогорова. Однако этот критерий можно применять только в том случае, когда гипотетическое распределение закона распределения полностью известно заранее из каких-либо теоретических соображений, т. е. когда известен не только вид закона распределения, но и все входящие в нее параметры.
. Простым критерием проверки гипотезы о виде закона распределения является критерий Колмогорова. Однако этот критерий можно применять только в том случае, когда гипотетическое распределение закона распределения полностью известно заранее из каких-либо теоретических соображений, т. е. когда известен не только вид закона распределения, но и все входящие в нее параметры.
Общая схема применения критерия Колмогорова может быть сформулирована следующим образом.
1. По результатам n независимых опытов определяют статистическую (опытную) функцию распределения ![]() .
.
2. Определяют величину D критерия Колмогорова:
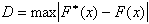
и вычисляют
![]() опыт=
опыт=![]() .
.
3. Принимают тот или иной уровень значимости ![]() критерия Колмогорова.
критерия Колмогорова.
4. Зная 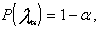 находят по таблице функции Колмогорова
находят по таблице функции Колмогорова ![]() соответствующее значение
соответствующее значение ![]() . Если
. Если ![]() опыт<
опыт<![]() гипотеза принимается. Если же
гипотеза принимается. Если же ![]() опыт>
опыт>![]() , гипотеза бракуется.
, гипотеза бракуется.
ПРИМЕР. В ОТК были измерены диаметры 60 валиков из партии, изготовленной на одном станке-автомате. Результаты измерения приведены в виде статистической совокупности:
Li
13,94 
14,04
14,04 
14,14
14,14 
14,24
14,24 
14,34
14,34 
14,44
14,44 
14,54
14,54 
14,64
14,64 
14,74
mi
1
1
4
![]()
![]()
![]()
![]()
6
Pi
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проверить с помощью критерия Колмогорова гипотезу о том, что выборка извлечена из генеральной совокупности, равномерно распределенной в интервале (13,94; 14,74), при уровне значимости 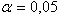 .
.
РЕШЕНИЕ. Функция распределения равномерно распределенной случайной величины Х в интервале (13,94; 14,74) имеет следующий вид:
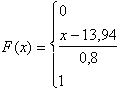 при
при 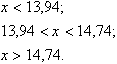
Пользуясь данными статистической совокупности, найдем значения статистической функции распределения ![]() . Определим также значения теоретической функции распределения F(x) и абсолютные значения разности
. Определим также значения теоретической функции распределения F(x) и абсолютные значения разности 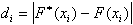 . Результаты вычисления представлены в таблице:
. Результаты вычисления представлены в таблице:
i
хi
F![]() (хi)
(хi)
F(х)
di
1
2
3
4
5
6
7
8
9
13,94
14,04
14,14
14,24
14,34
14,44
14,54
14,64
14,74
0
0,017
0,033
0,1
0,275
0,517
0,741
0,9
1
0
0,125
0,25
0,375
0,5
0,625
0,75
0,875
1
0
0,108
0,217
0,275
0,225
0,108
0,009
0,025
0
Сравнивая абсолютные величины разностей ![]() , определим
, определим
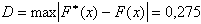 ,
,
и вычисляем:
![]() опыт=
опыт=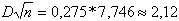 .
.
Зная  находим по таблице соответствующее
находим по таблице соответствующее ![]() =1,355. Так как
=1,355. Так как ![]() опыт=2,12>1,355, то выборка не согласуется с гипотезой.
опыт=2,12>1,355, то выборка не согласуется с гипотезой.
Рассмотрим применение к задаче проверки гипотез метода минимума риска. Общая постановка задачи такова.
Имеются две противоположные гипотезы ![]() и
и ![]() и некоторая связанная с ними случайная величина Х. Пусть х - числовое значение случайной величины Х, полученное в результате испытания;
и некоторая связанная с ними случайная величина Х. Пусть х - числовое значение случайной величины Х, полученное в результате испытания; ![]() - множество всех возможных значений случайной величины Х.
- множество всех возможных значений случайной величины Х.
Требуется произвести проверку гипотезы ![]() относительно конкурирующей гипотезы
относительно конкурирующей гипотезы ![]() на основании испытания, т. е. на основании полученного значения х случайной величины Х.
на основании испытания, т. е. на основании полученного значения х случайной величины Х.
Для решения поставленной задачи необходимо определить решающее правило разбиение множества ![]() возможных значений случайной величины Х на две части
возможных значений случайной величины Х на две части ![]() и
и ![]() с условием принятия гипотезы
с условием принятия гипотезы ![]() при попадании полученного значения х в результате опыта в
при попадании полученного значения х в результате опыта в ![]() и гипотезы Н
и гипотезы Н![]() при попадании х в
при попадании х в ![]() . Очевидно, что при этом всегда возможно допустить ошибку двоякого рода: ошибка первого рода - верна гипотеза Н
. Очевидно, что при этом всегда возможно допустить ошибку двоякого рода: ошибка первого рода - верна гипотеза Н![]() , а принято решение об истинности гипотезы Н
, а принято решение об истинности гипотезы Н![]() ; ошибка второго рода - верна гипотеза Н
; ошибка второго рода - верна гипотеза Н![]() , а принято решение об истинности гипотезы Н
, а принято решение об истинности гипотезы Н![]() .
.
Чтобы применить метод минимума риска к поставленной задаче, необходимо располагать следующими данными: ![]() - распределение случайной величины Х при условии, что верна гипотеза Н
- распределение случайной величины Х при условии, что верна гипотеза Н![]() ;
; ![]() - распределение случайной величины Х при условии, что верна гипотеза Н
- распределение случайной величины Х при условии, что верна гипотеза Н![]() ; р - доопытная вероятность того, что гипотеза Н
; р - доопытная вероятность того, что гипотеза Н![]() имеет место.
имеет место.
Оптимальное решающее правило, приводящее к наименьшему возможному риску в данной задаче, заключается в следующем: для полученного в результате опыта значения х вычисляется отношение
![]()
незываемое отношением правдоподобия, и сравнивается с числом
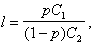
где ![]() - потери, связанные с ошибкой первого рода;
- потери, связанные с ошибкой первого рода;
![]() - потери, связанные с ошибкой второго рода.
- потери, связанные с ошибкой второго рода.
Если отношение ![]() меньше
меньше ![]() , применяется гипотеза Н
, применяется гипотеза Н![]() , в противном случае - Н
, в противном случае - Н![]() .
.
ПРИМЕР. На складе готовой продукции с двух заводов поступают партиями однотипные изделия. Качество продукции завода характеризуется вероятностью того, что наугад выбранное изделие является бракованным. Для одного завода р=0,16, для другого р=0,08. Потребитель наугад выбирает одну партию изделий. На основании результатов контроля решить, на каком заводе изготовлена выбранная партия изделий, если известно, что на складе храниться 8 партий изделий, из которых 5 изготовлено на втором заводе (р = 0,08).
Решение. Пусть Н![]() - гипотеза, состоящая в том, что выбранная партия изделий плохого качества (р=0,16); Н
- гипотеза, состоящая в том, что выбранная партия изделий плохого качества (р=0,16); Н![]() - противоположная гипотеза (р = 0,08).
- противоположная гипотеза (р = 0,08).
Отберем из партии наугад n изделий, среди которых оказалось m бракованных. Число бракованных есть случайная величина Х, подчиняющаяся биномиальному распределению. Поэтому при условии верности гипотезы Н![]()
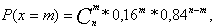
при условии верности гипотезы Н![]()
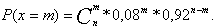
Отношение правдоподобия
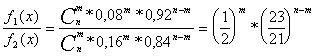
Доопытная вероятность того, что гипотеза Н![]() имеет место, равна
имеет место, равна ![]() .
.
Имеем
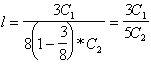 .
.
Составляем неравенство:
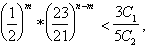
Откуда
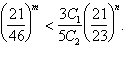
![]()
Определяя m из этого неравенства, имеем
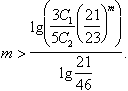
Итак, если число m бракованных изделий среди наугад выбранных изделий удовлетворяет этому неравенству, то принимается решение о плохом качестве полученной партии (верность гипотезы Н![]() ), в противном случае - решение о верности гипотезы H1.
), в противном случае - решение о верности гипотезы H1.
По своему назначению и характеру решаемых задач статистические критерии проверки гипотез чрезвычайно разнообразны. Однако их объединяет общность логической схемы, по которой они строятся. Коротко эту схему можно описать так.
1. Выдвигается гипотеза Н![]() .
.
2. Задаются величиной уровня значимости критерия ![]() .
.
Дело в том, что всякое статистическое решение, т. е. решение принятое на основании ограниченной выборки, неизбежно сопровождается, хотя может и очень малой, вероятностью ошибочного заключения. Выбор ![]() зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери от ошибочного отвержения гипотезы Н
зависит от сопоставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери от ошибочного отвержения гипотезы Н![]() , тем меньшей выбирается величина
, тем меньшей выбирается величина ![]() . На практике пользуются стандартными значениями уровня значимости: 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости
. На практике пользуются стандартными значениями уровня значимости: 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является величина уровня значимости ![]() Оно означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу при пользовании данным статистическим критерием.
Оно означает, что в среднем в пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу при пользовании данным статистическим критерием.
3. Задаются некоторой функцией от результатов наблюдений (критической статистикой) 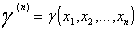 . Эта критическая статистика
. Эта критическая статистика ![]() , как и всякая функция от результатов наблюдения, сама является случайной величиной и в предложении справедливости гипотезы Н
, как и всякая функция от результатов наблюдения, сама является случайной величиной и в предложении справедливости гипотезы Н![]() подчинена некоторому хорошо изученному (затабулированному) закону распределения с плотностью
подчинена некоторому хорошо изученному (затабулированному) закону распределения с плотностью ![]() .
.
4. Из таблиц распределения ![]() находятся
находятся 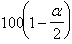 %-ная точка
%-ная точка ![]()
![]() и
и ![]() %-ная точка
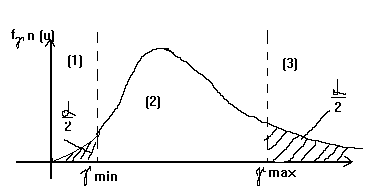
%-ная точка ![]() , распределяющие всю область возможных значений величины
, распределяющие всю область возможных значений величины ![]() на три области: область неправдоподобно малых (1), неправдоподобных больших (3) и правдоподобных (в условиях справедливости гипотезы Н
на три области: область неправдоподобно малых (1), неправдоподобных больших (3) и правдоподобных (в условиях справедливости гипотезы Н![]() ) (2) значений (рис.7).
) (2) значений (рис.7).
![]()
Рис. 7
В тех случаях, когда основную опасность для нашего утверждения представляют только односторонние отклонения, т. е. только "слишком малые" и только "слишком большие" значения критической статистики ![]() , находят лишь одну процентную точку: либо
, находят лишь одну процентную точку: либо ![]() %-ную точку
%-ную точку ![]() min, которая разделяет весь диапазон
min, которая разделяет весь диапазон ![]() на две части: область неправдоподобно малых и область правдоподобных значений; либо 100
на две части: область неправдоподобно малых и область правдоподобных значений; либо 100![]() %-ную точку
%-ную точку ![]() ; она будет разделять весь диапазон значений
; она будет разделять весь диапазон значений ![]() на область неправдоподобно больших и область правдоподобных значений.
на область неправдоподобно больших и область правдоподобных значений.
5. Наконец, в функцию ![]() подставляют имеющиеся конкретные выборочные значения случайной величины Х и подсчитывают численную величину
подставляют имеющиеся конкретные выборочные значения случайной величины Х и подсчитывают численную величину ![]() . Если окажется, что вычисленное значение принадлежит области правдоподобных значений
. Если окажется, что вычисленное значение принадлежит области правдоподобных значений ![]() , то гипотеза Н
, то гипотеза Н![]() считается непротиворечащей выборочным данным. В противном случае, т. е. если
считается непротиворечащей выборочным данным. В противном случае, т. е. если ![]() слишком мала или слишком велика, делается вывод, что
слишком мала или слишком велика, делается вывод, что ![]() не подчиняется закону
не подчиняется закону ![]() (этот вывод, как видно из рис.7, сопровождается ошибкой
(этот вывод, как видно из рис.7, сопровождается ошибкой ![]() ), и это несоответствие мы вынуждены объяснить ошибочностью высказанного нами предположения Н
), и это несоответствие мы вынуждены объяснить ошибочностью высказанного нами предположения Н![]() и, следовательно, отказаться от него.
и, следовательно, отказаться от него.
Выводы
1. Процедура обоснованного сопоставления высказанного исследователем предположительного утверждения (гипотезы) относительно природы или величины неизвестных параметров рассматриваемой случайной величины с имеющимися в его распоряжении результатами наблюдения осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотезы.
2. По своему содержанию высказываемые в ходе статистической обработки данных гипотезы подразделяются на следующие типы:
- об общем виде закона распределения исследуемой случайной величины;
- об однородности двух или нескольких обрабатываемых выборок;
- о числовых значениях параметров исследуемой генеральной совокупности;
- об общем виде зависимости, существующей между компонентами исследуемого многомерного признака;
- о независимости и стационарности ряда наблюдений.
3. Все статистические критерии строятся по общей логической схеме. Построить статистический критерий - это значит:
а) определить тип проверяемой гипотезы;
б) предложить и обосновать конкретный вид функции от результатов наблюдений (критической статистики ![]() ), на основании значений которой принимается окончательное решение;
), на основании значений которой принимается окончательное решение;
в) указать такой способ выделения из области возможных значений критической статистики области отклонения проверяемой гипотезы Н![]() , чтобы было соблюдено требование к величине ошибочного отклонения гипотезы Н
, чтобы было соблюдено требование к величине ошибочного отклонения гипотезы Н![]() (т. е. к уровню значимости критерия
(т. е. к уровню значимости критерия ![]() ).
).




