Федеральное агентство по образованию

Бийский технологический институт (филиал)

государственного образовательного учреждения

высшего профессионального образования

«Алтайский государственный технический университет

имени »

планирование перевозок автомобильным транспортом при проектировании
логистических информационных систем

Методические рекомендации для студентов специальности 080801 «Прикладная информатика в экономике» всех форм обучения,
изучающих курс «Транспортное обеспечение

деятельности предприятий»

Бийск

Издательство Алтайского государственного технического университета

им.

  2010

УДК 339.18:681.3.06

Ф24

Рецензент:

к. э.н., с. н.с. (Институт экономики и организации промышленного производства СО РАН).

Работа подготовлена на кафедре ИУС

Фарков, А. Г.

Ф24

Планирование перевозок автомобильным транспортом при проектировании логистических информационных систем: мето-дические рекомендации для студентов специальности 080801 «Прикладная информатика в экономике» всех форм обучения,
изучающих курс «Транспортное обеспечение деятельности пред-приятий» / ; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2010. – 29 с.

Приведена методика расчета основных параметров работы автомобильного транспорта в соответствии с действующими стандартами, даны основные методы планирования и оптимизации маршрутов автотранспорта.

Методические рекомендации предназначены для студентов всех форм обучения, изучающих курс «Транспортное обеспечение деятельности предприятий».

УДК 339.18:681.3.06

Ф24

Рассмотрены и одобрены

на заседании кафедры ИУС.

Протокол № 12 от 01.01.2001 г.

© , 2010

 

© БТИ АлтГТУ, 2010

1 Расчет технико-экономических параметров работы Автомобильного транспорта

Работа автомобильного транспорта может быть оценена на основе системы показателей, характеризующих количество и качество выпол-ненной работы. К ним относятся следующие показатели:

- Коэффициент списочной готовности парка автомобилей за один рабочий день

где – числов автомобилей, готовых к эксплуатации;

– списочное число автомобилей.

- Коэффициент выпуска автомобилей за один рабочий день

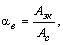
где – число автомобилей, эксплуатируемых предприятием.

- Коэффициент статического использования грузоподъемности

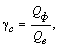
где – масса фактически перевезенного груза, т;

– масса груза, которая могла бы быть перевезена, т.

- Коэффициент динамического использования грузоподъемности

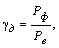
где – фактически выполненная транспортная работа, т-км;

– возможная транспортная работа, т-км.

- Коэффициент использования пробега

,

где – груженый пробег, км;

– общий пробег, км;

– первый нулевой пробег, км;

– холостой пробег, км;

– второй нулевой пробег, км.

- Среднее расстояние ездки с грузом

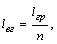
где – число ездок.

- Среднее расстояние перевозки

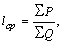
где – транспортная работа, т-км;

– объем перевозок, т.

- Техническая скорость

,

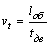где – время движения, ч.

- Эксплуатационная скорость

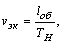
где – время в наряде, ч.

- Количество ездок

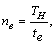
где – время одной ездки, ч.

- Время одной ездки

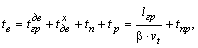
где – время движения груженого автомобиля, ч;

– время движения без груза, ч;

– время погрузки груза, ч;

– время разгрузки груза, ч;

– время простоя автомобиля под погрузкой и разгрузкой, ч.

- Производительность подвижного состава

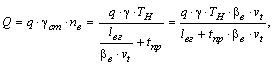
где – грузоподъемность, т;

– статический коэффициент использования грузоподъемности;

– коэффициент использования пробега.

2 ПЛАНИРОВАНИЕ МАРШРУТОВ ДВИЖЕНИЯ АВТОТРАНСПОРТА

Движение автотранспорта происходит по маршрутам. Мар­шрут движения – путь следования автомобиля при выполнении перевозок.

Основные элементы маршрута: длина маршрута – путь, проходимый автомобилем от начального до конечного пунк­та маршрута; оборот автомобиля – законченный цикл движе­ния, т. е. движение от начального до конечного пункта и обрат­но; ездка – цикл транспортного процесса, т. е. движение от на­чального до конечного пункта.

Основные элементы маршрута показаны на рисунке 1.

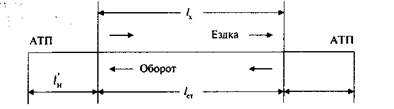
Рисунок 1 – Основные элементы маршрута

Расстояние, на которое транспортируется груз за ездку, на­зыва-ется длиной ездки с грузом ().

Маршруты движения могут быть маятниковые и кольцевые. Схемы маятниковых маршрутов показаны на рисунке 2. При маятниковом маршруте путь следования автомобиля между двумя грузопунктами неоднократно повторяется.

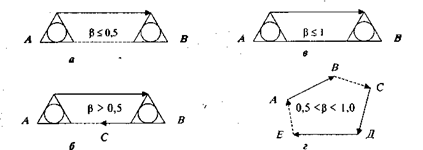
– коэффициент пробега автомобиля на маршруте;

а – с обратным холостым пробегом; б – с обратным
не полностью груженым пробегом; в – с обратным груженым
пробегом; г – кольцевой маршрут

Рисунок 2 – Схемы маршрутов

Кольцевой маршрут – маршрут движения автомобиля по замк­ну-тому контуру, соединяющему несколько потребителей (по­ставщиков).

Разновидностями кольцевых маршрутов явля­ются развозочные, сборные и сборно-развозочные маршруты.

Развозочным называется такой маршрут, при котором продук­ция загружается у одного поставщика и развозится нескольким потребителям. Сборный маршрут – это маршрут движения, когда продукция получается у нескольких поставщиков и доставляется одному потребителю. Сборно-развозочный маршрут – это соче­тание развозочного и сборного маршрутов.

Технико-экономические показатели маятникового маршрута с обратным холостым пробегом рассчитываются по формулам

,

,

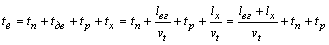где – время ездки автомобиля, ч;

– время оборота автомобиля, ч;

– время погрузки автомобиля, ч;

– время разгрузки автомобиля, ч;

– время движения автомобиля без груза, ч;

– расстояние груженой ездки, км;

– расстояние ездки без груза, км;

– техническая скорость.

Суточный объем перевозок по массе, т,

.

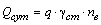Суточный грузооборот, т-км,

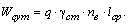
Время работы автомобиля на маршруте

,

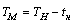где – время автомобиля в наряде, ч;

– время, затраченное на нулевой пробег, ч.

Технико-экономические показатели маятникового маршрута с обратным не полностью груженным пробегом рассчитываются по формулам

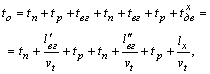
где , – расстояния груженых ездок 1 и 2 соответственно, км.

При перевозке однородного груза

,

,

где – количество оборотов на маршруте.

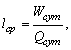
Технико-экономические показатели маятникового маршрута с обратным полностью груженным пробегом рассчитываются по фор-мулам

где – время нахождения автомобиля в движении, ч;

– время нахождения автомобиля в простое, ч.

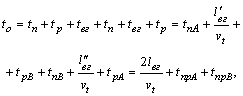
где – время ездки груженой, ч;

, , , – время погрузки, разгрузки в пунктах , соответственно, ч;

, – время погрузки-разгрузки в пунктах , соответст-венно, ч.

При перевозке однородного груза

,

,

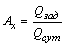где – коэффициент загрузки автохозяйства;

– заданная производительность,

где – длина нулевого пробега, км;

Технико-экономические показатели кольцевого маршрута рассчи-тываются по следующим формулам:

- Время оборота подвижного состава на кольцевом маршруте

где – длина маршрута, км;

- Количество оборотов автомобиля за время работы на маршруте

,

где – время работы автомобиля на маршруте, ч,

,

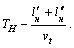
где – количество груженых ездок за оборот.

- Дневная выработка автомобиля

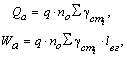
где – средняя длина груженой ездки за оборот, км,

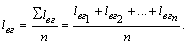
- Среднее расстояние перевозки за оборот, км,

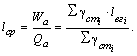
- Среднее время простоя под погрузкой-разгрузкой каждую ездку за оборот, ч,

- Средний коэффициент статического использования грузоподъ-емности за оборот

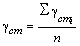
или

где – масса погружаемого в каждом пункте груза, т.

- Время оборота автомобиля на развозочном маршруте

,

где – время за каждый заезд, ч;

– количество заездов.

3 Оптимизация маршрутов движения

автомобильного транспорта

Решение задач оптимизации маршрутов движения автомобиль-ного транспорта имеет большое значение в выстраивании всей логис-тической цепочки, решении основных задач транспортной логистики. Поиск оптимального варианта доставки груза из множества возможных является одной из наиболее сложных задач логистики. Как правило, такие задачи невозможно решать на основе опыта или же простейши-ми арифметическими методами. На самом деле, при наличии несколь-ких поставщиков или потребителей продукции, для каждого из кото-рых имеется несколько альтернативных маршрутов доставки грузов, число возможных вариантов транспортировки может составлять от не-скольких десятков до нескольких тысяч.

Планирование работы автомобильного транспорта до недавних пор было возможно, как правило, лишь на основе детерминированных моделей линейного программирования. В настоящее время становится возможным в некоторых случаях применение динамического прог-раммирования при планировании работы автотранспорта. Как правило, системы управления грузоперевозками, использующие модели динами-ческого программирования, базируются на непрерывном, с заданными интервалами во времени, обновлении информации о фактическом местонахождении транспортного средства с помощью GPS – систем навигации. Однако даже использование таких средств не устраняет в полной мере проблем, связанных с невозможностью точного прогно-зирования работы автомобильного транспорта. Главной причиной этому является то, что изменения, учитываемые в течение смены, при работе единичного автомобиля на маршруте, весьма трудно учитывать при планировании перевозок. Поэтому в настоящее время модели ди-намического программирования имеют весьма ограниченное примене-ние при планировании регулярных, многократно повторяющихся пере-возок. В частности, они находят свое применение на городском обще-ственном транспорте. В общем же случае планирования и оптимизации автоперевозок основным инструментальным средством по-прежнему остается детерминированная модель линейного программирования, описывающая процесс перевозок, без учета возможных временных изменений. Практикой доказано, что это инструментальное средство является вполне достаточным для планировании 90 % автоперевозок.

На автомобильном транспорте методом линейно­го программиро-вания решают такие задачи:

• отыскание оптимального числа ездок автомобилей на мар­шру-тах при установленном времени пребывания в наряде (задача на минимальные потери рабочего времени);

• отыскание оптимального варианта закрепления получателей за поставщиками однородной продукции (задача на мини­мум нулевых пробегов);

• составление рациональных маршрутов работы подвижно­го сос-тава – увязка ездок (задача на минимум холостых пробегов);

• организация развозочных и сборочных маршрутов (задача на определение минимального пробега при объезде грузопунктов);

• распределение подвижного состава и погрузочно-разгрузочных средств по маршрутам работы (задача на максималь­ное использование рабочего времени автомобилей и погрузочно-разгрузочных механизмов и др.).

Все перечисленные задачи базируются на математическом моде-лировании изучаемого процесса, т. е. на описании количе­ственных
закономерностей этого процесса с помощью матема­тических выражений (математической модели). Математическая модель, как уже было сказано, является абстрактным изображе­нием реального процесса и в меру своей абстрактности может его характеризовать более или менее точно.

Одной из основных задач в логистической системе является ра-счет рациональных маршрутов перевозки и со­ставление оптимальных графиков (расписаний) доставки продук­ции потребителям, т. е. ответ на вопросы, когда, сколько и в какое время должны быть доставлены грузы.

Вариантами организации движения автомобиля могут быть: ма-ятниковый маршрут с обратным порожним пробегом или развозоч-ный маршрут при перевозке мелкопартионных грузов потреби­телям. Подробно рассмотрим организацию этих маршрутов.

3.1 Маятниковый маршрут с обратным порожним пробегом

На практике при планировании работы автомобилей по маят­нико-вым маршрутам с обратным холостым пробегом часто руководству­ют-ся единственным правилом: последний пункт разгрузки авто­мобилей должен быть как можно ближе к автохозяйству. Счита­ется, что при соблюдении этой основанной на здравом смысле рекомендации обес-печивается минимум пробега без груза. Анализ рассматриваемой зада-чи методом линейного программирования показал, что такое решение совсем неочевидно. Для доказатель­ства рассмотрим пример.

Пример 1. Допустим, что с базы необходимо доставить про­ду-кцию потребителям и. К обоим потребителям автомобиль может сделать за время в наряде две ездки. Необходимо составить маршрут движения автомобиля, обеспечивающий минимум порож­него пробега.

Условия задачи, схема размещения потребителей, на примере решения которой составляется маршрут движения, приведены на ри-сунке 3.

При решении этой задачи могут возникнуть два случая:

1) продукция поставляется в пункт, а затем в , из автомо­биль поступает в АТП (пункт );

2) продукция поставляется в пункт , а потом в , из автомо­биль возвращается в АТП (пункт ).

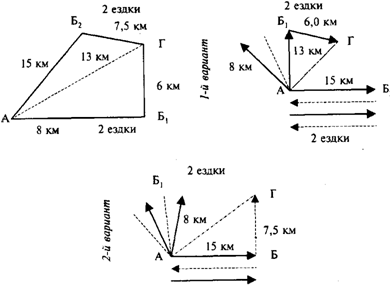
Рисунок 3 – Схемы размещения потребителей

Для выбора варианта перевозки продукции произведем расчет коэффициента использования пробега автомобиля D и полученные значения сведем в таблицу 1. Как видно из таблицы, наиболее эффек-тивен второй вариант, поскольку коэффициент использования пробега во втором случае выше, чем в первом. Однако если руководствоваться правилом, что наименьший про­бег достигается, когда первый пункт погрузки и последний пункт разгрузки находятся поблизости от авто-транспортного предприятия, целесообразен первый вариант. Чтобы проверить правильность вы­бора, решим задачу математическим мето-дом. Задача составления рациональных маршрутов, обеспечивающих минимальный порожний пробег транспортных средств, сводится к следующей задаче линейного программирования:

Минимизировать линейную формулу

при условиях

и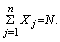

где – порожний пробег, км;

– расстояние от пункта назначения до автотранспорт­ного предприятия (второй нулевой пробег), км;

– расстояние от до (груженый пробег), км;

– номер (индекс) потребителя (= 1, 2, ..., );

– количество автомобилей, работающих на маршрутах с пос-ледним пунктом разгрузки ;

– объем перевозок (в ездках автомобиля);

– число автомобилей, работающих на всех маршрутах.

Допустим, что пункты назначения занумерованы в порядке воз­растания разностей

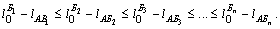
Тогда оптимальное решение таково:

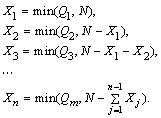
Решая эту задачу, мы должны знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное
чис­ло автомобилей заканчивает работу в пунктах назначения с ми-
ни­мальными разностями второго нулевого и груженого пробегов.

Для решения задачи необходимо исходные данные записать в специальную таблицу, с помощью которой произвести все необхо­димые вычисления по составлению маршрутов (см. таблицу 1).

Таблица 1 – Исходные данные

Пункт назначения

Количество груженых ездок

Столбец разностей

…

…

…

…

…

…

Для каждого пункта назначения, т. е. по каждой строке, рассчи­тывают алгебраические разности

,

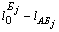которые записывают в соответствующие клетки столбца разностей.

Рассмотрим применение предложенного алгоритма на при­мере, воспользовавшись исходными данными, приведенными на рисунке 4.

Исходя из этих условий составляем таблицы объема перевозок и ездок и расстояния перевозок (таблицы 2, 3).

Таблица 2 – Объем перевозок (ездки)

Пункт отправления

Пункт назначения

2

2

Таблица 3 – Расстояние перевозок, км

Пункт
отправления

АТП

Пункт назначения

13

8

15

-

6

7,5

Составляем рабочую матрицу условий (таблица 4), используя данные таблиц, и решаем ее.

Таблица 4 – Рабочая матрица условий

Пункт назначения

(пункт отправления)

Столбец разностей (оценка)

6

8

-2

2

7,5

15

-7,5

2

Наименьшую оценку (-7,5) имеет пункт , в который нуж­но сделать две ездки. Принимаем его последним пунктом мар­шрута
––, т. е. получаем маршрут варианта II.

В таблице 5 приведены коэффициенты использования пробега автомобиля по вариантам.

Таблица 5 – Коэффициент использования пробега автомобиля

по вариантам

Показатель

Вариант I

Вариант II

Пробег, км:

общий

103,0

97,5

порожний

57,0

51,5

груженый

46,0

46,0

Коэффициент использова­ния пробега

0,44

0,47

Пример 2. Рассчитать рациональные маятниковые маршруты и составить графики доставки продукции потре­бителям при объемах, указанных в таблице 6, расстояниях и затратах времени на одну ездку, указанных в таблицах 7, 8.

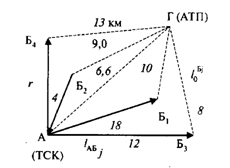
Г – А – автохозяйство – ТСК, первый нулевой пробег, 6,6 км
(в расчетах показатель учтен при определении времени
работы автомобиля на маршруте)

Рисунок 4 – Схема размещения автохозяйства, ТСК и потребителей

Таблица 6 – Расстояние, км

Пункт оправления и АТП

АТП

Пункт назначения

6,6

18

4

12

7

-

10

9

8

13

Таблица 7 – Объем перевозок (ездки)

Пункт отправления

Пункт назначения

Объем перевозок

Объем перевозок за одну ездку, т

Количество ездок

21,0

7,0

3

196,0

7,0

28

42,0

7,0

6

175,0

7,0

25

Итого:

434,0

7,0

62

Известны: время работы автомобиля на маршруте = 460 мин; техническая скорость = 20 км/ч; простой под погрузкой и раз­грузкой

= 30 мин.

Схема размещения ТСК, автохозяйства приведена на рисунке 4.

Решение

Формулы расчета затрат времени в минутах на одну ездку для маршрутов 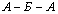, 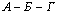и расчет времени и :

1) .

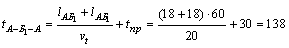Так же рассчитываются затраты времени и для других ездок по мар­шруту .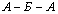

2) ,

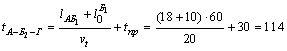где – груженый пробег, обозначение в расчетах

– второй нулевой пробег, обозначение в расчетах

Так же рассчитываются затраты времени и для других ездок по мар­шруту .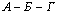

В таблице 8 приведены затраты времени на одну ездку в минутах.

Таблица 8 – Затраты времени на одну ездку

138

114

54

69

102

90

72

90

Для дальнейших расчетов составим схему размещения автохо­зяйства (АТП), транспортно-сбытового комплекса (ТСК) и по­требителей . Укажем расстояние перевозки от автохозяйства до ТСК (), от ТСК до потребителей потребителей до автохозяйства

Для решения составим рабочую матрицу I.

Наименьшую оценку (-8) имеет пункт , а наибольшую оцен­ку –пункт , поэтому начальным пунктом обслуживания будет пункт , а – пункт, из которого автомобиль будет возвращаться в автохозяй-ство.

Маршрут 1 для одного автомобиля: 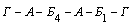. Нам известно, что = 460 мин. Если автомобиль обслужит пункт и возвратится в автохозяйство , то он затратит 114 мин (см. табли-
цу 9, 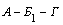). Следовательно, на обслуживание пункта оста-лось 346 мин, т. е. (460 – 114) мин, если затраты времени на ездку равны 72 мин (см. таблицу 9), то в пункт авто­мобиль сделает примерно 5 ездок . Три автомобиля обеспечат пункт (три ездки), а в пункт необходимо сделать 15 ездок (3´5).

Таблица 9 – Рабочая матрица I

Пункт
назначения

Исходные данные

Оценка (разность расстояния)

10

18

10–18 = -8

3

9

4

9–4 = +5

28

8

12

8–12 = -4

6

13

7

13–7 = +6

25

После расчетов составляем рабочую матрицу II (таблица 10) с учетом выполненной работы на маршруте 1.

Таблица 10 – Рабочая матрица II

Пункт назначения

Исходные данные

Оценка (разность расстояния)

9

4

+5

28

8

12

-4

6

13

+6

25–15 = 10

Маршрут 2 получаем при тех же рассуждениях 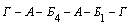. С помощью двух автомобилей можно обслу-жить пункт , сделав 10 ездок, а в пункт , сделав 4 ездки.

В таблице 11 представлена рабочая матрица III для составления маршрута 3.

Маршрут 3: . Для этого маршрута при­ни-маем четыре автомобиля, которые сделают четыре ездки в пункт и 28 ездок в пункт .

Таблица 11 – Рабочая матрица III

Пункт назначения

Исходные данные

Оценка (разность расстояния)

3

9

4

+5

28

8

12

-4

4

Сводная маршрутная ведомость представлена в таблице 12.

Таблица 12 – Сводная маршрутная ведомость

Маршрут

Обозначение

Показатели маршрута

кол-во ездок

объем перево-зок, т

кол-во автомо-
билей

коэффициент использования
пробега

1

2

3

4

5

6

1

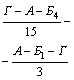
18

126

3

0,5

Продолжение таблицы 12

1

2

3

4

5

6

2

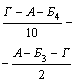
12

84

2

0,5

3

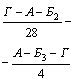
32

224

4

0,5

Итого:

62

434

9

0,5

3.2 Развозочный маршрут при перевозке мелкопартионных

гру­зов потребителям

Постановка задачи. Заданы пункты потребления ( i = 1, 2,…n).

Груз необходимо развезти из начального пункта (склад) во все ос-тальные (потребители). Потребность пунктов потреб­ления в объеме поставки составляет В начальном пункте имеются транс-портные средства в количестве грузоподъ­емностью

Известно также расстояние перевозки между потребителями. При решении задачи необходимо учитывать, что количество транс-портных средств должно быть больше, чем пунктов потреб­ления
{>); в начальном пункте (склад) продукции долж­но быть боль-ше или равно сумме потребностей всех потребителей

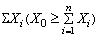
Для каждой пары пунктов определяем расстояния перевоз-ки . Это расстояние должно быть больше или равно нулю, т. е. .

Схема размещения пунктов и расстояния между ними приведе­ны на рисунке 5.

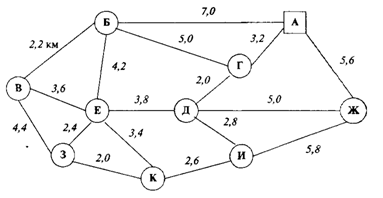
Рисунок 5 – Схема размещения пунктов и расстояния между ними

Требуется найти замкнутых путей из единственной общей точки так, чтобы выполнялось условие

Решение

Этап I. Строим кратчайшую сеть, связывающую все пункты без замкнутых контуров {«минимальное дерево»), рисунок 6.

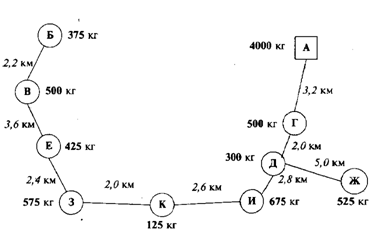
Рисунок 6 – Кратчайшая связывающая сеть {«минимальное дерево»)

Затем по каждой ветви сети, начиная с пункта, наиболее уда­ленного от начального пункта (считая по кратчайшей связываю­щей сети), группируем пункты на маршрут с учетом количества ввозимого груза и грузоподъемности единицы подвижного состава. Ближайшие к другой ветви пункты группируем вместе с пунктами данной ветви.

Исходя из данной грузоподъемности подвижного состава все пун-кты можно сгруппировать так, как показано в таблице 13. Сгруппиро-вав пункты по маршрутам, переходим к следующему этапу расчетов.

Таблица 13 – Группировка маршрутов исходя из грузоподъемности автомобиля

Маршрут I

Маршрут II

Пункт

Объем завоза, кг

Пункт

Объем завоза, кг

375

525

500

300

425

675

575

500

125

-

-

Итого:

2000

Итого:

2000

Этап II. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу (таблица 14), в которой по диагонали размещаем пункты, включаемые в мар­шрут, и начальный пункт , а в соответствующих клетках – крат­чайшие рас-стояния между ними. Для примера матрица принята симметричной, хотя приведенный ниже способ применим для решения и несиммет-ричных матриц. Каждый пункт потребления обслуживается подвиж-ным составом одного типа (автомобиль грузоподъемностью 2,5 т); груз 2-го класса; a = 0,8.

Начальный маршрут строим для трех пунктов матрицы, имею­щих наибольшие размеры сумм, показанных в строке (47,2; 30,0; 27,6), т. е. , , . Для включения последующих пунктов выбираем из остав-шихся пункт, имеющий наибольшую сумму, например, пункт (сумма 26,8), и решаем, между какими пунктами его следу­ет включать, т. е. между и , и или и .

Таблица 14 – Матрица для определения рационального порядка объезда пунктов

Номер

строки

7,0

9,2

9,0

11,4

10,6

1

7,0

2,2

4,2

6,6

7,6

2

9,2

2,2

3,6

4,4

6,4

3

9,0

4,2

3,6

2,4

3,4

4

11,4

6,6

4,4

2,4

2,0

5

10,6

7,6

6,4

3,4

2,0

S

47,2

27,6

25,8

22,6

26,8

30,0

Чтобы это решить, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле

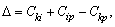
где – расстояние, км;

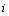– индекс включаемого пункта;

– индекс первого пункта из пары;

– индекс второго пункта из пары.

При включении пункта между первой парой пунктов и определяем размер приращения в км при условии, что = 3;
= ; =.

Тогда

Подставляем значения из таблицы 13.

Получаем, что

.

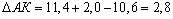Таким же образом определяем приращение в км (если
пункт включить между пунктами и )

Из полученных значений выбираем минимальное, т. е. = 1,0. Следовательно, пункт должен быть между пунктами и . Получаем маршрут вида .

Используя этот метод и формулу приращения, определяем, ме­жду какими пунктами следует расположить пункты и . Начнем с
, так как размер суммы (см. таблицу 14) этого пункта больше
(25,8 > 22,6). Итак, приращение (в км) равно

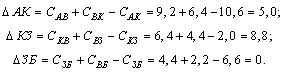
В том случае, когда = 0, для симметричной матрицы расчеты можно не продолжать, так как значение, меньшее, чем 0, получено быть не может. Поэтому пункт должен быть между пунктами и . Тогда маршрут получит вид .

В результате проведенного расчета включаем следующий пункт между пунктами и , так как для этих пунктов получено мини­мальное приращение 1,6.

Таким образом, окончательный порядок движения по маршру­ту I будет .

Таким же методом определяем кратчайший путь объезда пун-
ктов по маршруту II. В результате расчетов получим маршрут длиной 19,4 км.

Порядок движения по маршрутам I и II приведен на рисунке 7.

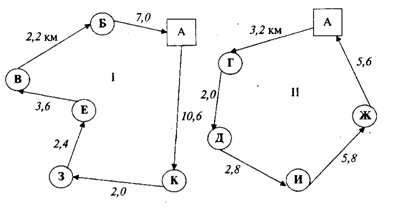
Рисунок 7 – Порядок движения по маршрутам I и II

СПИСОК ЛИТЕРАТУРЫ

1. Бауэрсокс, Д. Дж. Логистика. Интегрированная цепь поставок / Д. Дж. Бауэрсокс, Д. Дж. Клосс. – М.: Олимп-Бизнес, 2001. – 900 с.

2. Гаджинский, : учебник / . – 4-е изд. – М.: Маркетинг, 2001. – 455 с.

3. Дыбская, складирования / . – М.: ГУ-ВШЭ, 1999. – 180 с.

4. Камовников, : учебное пособие / -ков [и др.]. – М.: Изд. ун-та РАО, 2000. – 120 с.

5. Козлов, фирмы / , . – СПб.: СПбГУЭФ, 1998. – 108 с.

6. Колобов, промышленной логистики / -бов, . – М.: МГТУ им. , 1998. – 255 с.

7. Лукинский, автомобильного транспорта /
. – М.: Финансы и статистика, 2000. – 480 с.

8. Миротин, логистика: учеб. пособие /
, . – М.: Брандес, 1996. – 285 с.

9. Невзоров, и эксплуатация грузоподъемных кранов / , . – М.: Транспорт, 2000. – 448 с.

10. Неруш, : учебник / . – 3-е изд. –М.: ЮНИТИ-ДАНА, 2003. – 495 с.

11. Новиков, : учеб. пособие / ,
. – СПб.: Бизнес-пресса, 1999. – 280 с.

12. Основы логистики: учеб пособие / под. ред. и . – М.: ИНФРА-М, 1999. – 520 с.

13. Промышленный транспорт / под. ред. . – М.: Транспорт, 1974. – 650 с.

14. Рейфе, развития логистической деятельно-сти на оптовом рынке / . – СПб.: СПбУЭФ, 1996. – 95 с.

15. Саркисов, логистикой / – М.: ИНФРА-М, 2001. – 170 с.

16. Смехов, транспортной логистики / . – М.: Транспорт, 1995. – 340 с.

17. Стаханов, логистика: учеб. пособие / , . – Ростов-на-Дону: РГСУ, 1999. – 153 с.

18. Шевалье, Ж. Логистика. Новые принципы менеджмента и конкурентоспособности / пер. с фр.; Ж. Шевалье, Т. Вань – М.: Консалтбанкир, 1997. – 805 с.

СОДЕРЖАНИЕ

1 расчет технико-экономических параметров работы автомобильного транспорта………………….

2 планирование маршрутов движения автотранспорта…………………………………………...….…

3 оптимизация маршрутов движения автомобильного транспорта……………………………...

3.1 Маятниковый маршрут с обратным порожним

пробегом………………………………………………………..

3.2 Развозочный маршрут при перевозке мелкопартионных

гру­зов потребителям…………………………………………...

список литературы…………………………………………….

3

5

10

12

21

27

Учебное издание

Фарков Андрей Георгиевич

планирование перевозок автомобильным транспортом при проектировании
логистических информационных систем

Методические рекомендации для студентов специальности 080801 «Прикладная информатика в экономике» всех форм обучения,
изучающих курс «Транспортное обеспечение

деятельности предприятий»

Редактор

Технический редактор

Подписано в печать 15.01.10. Формат 60´84 1/16

Усл. п. л. 1,67. Уч.-изд. л. 1,81

Печать – ризография, множительно-копировальный

аппарат «RISO TR -1510»

Тираж 50 экз. Заказ 2010-04

Издательство Алтайского государственного

технического университета

г. Барна

Оригинал-макет подготовлен ИИО БТИ АлтГТУ

Отпечатано в ИИО БТИ АлтГТУ

7