МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
проф.
1/2 года, 2 курс, факультет психологии
1. Графики и квантили распределения вероятностей числа успехов 
в 
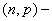испытаниях Бернулли. Применение таблицы А.2 из [1].
2. Схема проверка гипотезы 
: 
против альтернативы 
: 
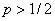(либо против альтернативы : 
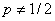) с использованием таблицы A из [2]. Приложение этой схемы для следующих моделей:
а) биномиальный критерий [2, c. 35-36];
б) критерий значимости изменений [2, c. 57-59];
в) критерий знаков [2, c. 97-98].
3. Схема и примеры проверки гипотезы : 
против альтернативы : 
с применением таблиц биномиальных вероятностей [1, c. 32-33], [2, c. 36-37].
4. Непрерывная случайная величина, плотность распределения, функция распределения. Математическое ожидание, дисперсия и их свойства.
5. Стандартное нормальное распределение, квантили. Нормальное распределение 
.
6. Формулировка закона больших чисел [4, c. 122 и 73-75].
7. Выборка, выборочные характеристики и их связь с теоретическими [4, c.124-128].
8. Вычисление математического ожидания и дисперсии оценки 
[4, c. 75].
9. Построение доверительного интервала для неизвестного математического ожидания при известной дисперсии.
10. Построение доверительного интервала для неизвестной дисперсии нормальной выборки при известном математическом ожидании. Распределение 
(хи-квадрат) и его квантили.
11. Построение доверительных интервалов для неизвестных математического ожидания и дисперсии нормальной выборки. Распределение Стьюдента и его квантили.
12. Построение непараметрического доверительного интервала для теоретического среднего выборки с помощью квантилей знаковых рангов Вилкоксона [1, c. 53-55].
13. Приближенное вычисление квантилей (критических значений) с помощью центральной предельной теоремы. Примеры – биномиальное распределение, распределение , распределение Манна-Уитни, распределение знаковых рангов Вилкоксона, распределение Кендэлла. Сравнение приближенных значений с табличными.
14. Проверка гипотезы однородности двух независимых нормальных выборок по критерию Стьюдента [3, c. 53]. Построение доверительного интервала для параметра сдвига.
15. Проверка гипотезы однородности двух независимых выборок по критерию Манна-Уитни. Доверительный интервал для параметра сдвига [1, c. 93-96].
16. Однофакторный дисперсионный анализ. Критерий Джонкхиера [1, c. 136-137].
17. Критерий знаковых рангов Вилкоксона для проверки эффективности обучения с помощью метода, использующего однородные пары испытуемых [1, c. 46-47] и [2, c. 100‑102].
18. Метод наименьших квадратов для вычисления оптимальных параметров регрессионной прямой.
19. Линейная регрессия с нормальными ошибками (параметрическая модель). Доверительные интервалы.
20. Непараметрическая линейная регрессия. Метод угловых наклонов Тейла. Доверительные интервалы [1, c. 219-221].
21. Корреляционный анализ. Проверка гипотезы о независимости двух признаков:
а) параметрическая модель нормальной корреляции (поле корреляций, выборочный коэффициент корреляции, преобразование Фишера) [6];
б) непараметрическая модель (критерий Спирмена, таблица сопряженности признаков) [1, 6].
Литература
Все материалы по курсу подробно опубликованы на сайте: http://www. stat-msu. .
1. Непараметрические методы статистики. М., Финансы и статистика, 1983.
2. Справочник по непараметрической статистике. М., Финансы и статистика, 1982.
3. Артемьева задач по теории вероятностей и математической статистике для психологов. М., изд-во МГУ, 1969.
4. Дьячков вероятностей. Лекции. М., изд-во МГУ, 1980.
5. , Михайлевская практикум по психологии. М., изд-во МГУ, 1983.
6. , Смирнов математической статистики. М., Наука, 1965.
7. , Макаров данных на компьютере. М., Финансы и статистика, 1995.
