Модели оценки доходности активов

Лекция 20. Модели оценки доходности активов

Ключевые понятия

Модель САРМ

Линия рынка капитала – CML

Рыночный (системный) риск

Нерыночный риск

Бета

Агрессивные и защитные активы

Линия рынка актива – SML

Альфа

Доходность портфеля

САРМ при неравных ставках по займам и депозитам

САРМ с нулевой бетой

САРМ для облигаций

САРМ для фьючерсов

САРМ для опционов

Модель Шарпа

Линия характеристики

Коэффициент детерминации

Содержание:

20.1. МОДЕЛЬ ОЦЕНКИ СТОИМОСТИ АКТИВОВ (CAPM) …………………….. 2

20.1.1. Линия рынка капитала ………………………………………………………….. 2

20.1.2. Рыночный и нерыночный риски ………………………………………………. 4

20.1.3. Бета ………………………………………………………………………………… 6

20.1.4. Линия рынка актива …………………………………………………………….. 8

20.1.5. Вопросы, возникающие при построении SML ……………………………….. 10

20.1.6. CML и SML ………………………………………………………………………... 11

20.1.7. Альфа ………………………………………………………………………………. 12

20.2. МОДИФИКАЦИИ САРМ …………………………………………………………. 14

20.2.1. САРМ для случая, когда ставки по займам и депозитам не равны ……….. 14

20.2.2.САРМ с нулевой бетой …………………………………………………………… 15

20.2.3. Версия САРМ для облигаций …………………………………………………… 15

20.2.4. Версия САРМ для фьючерсных контрактов ………………………………… 16

20.2.5. Версия САРМ для опционов …………………………………………………… 17

20.3.МОДЕЛЬ ШАРПА ………………………………………………………………… 19

20.4. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ ………………………………………… 21

20.5. САРМ И МОДЕЛЬ ШАРПА ……………………………………………………… 23.

20.6. ОПРЕДЕЛЕНИЕ НАБОРА ЭФФЕКТИВНЫХ МОДЕЛЕЙ …………………. 24

20.7. МНОГОФАКТОРНЫЕ МОДЕЛИ ………………………………………………. 25

20.1. Модель стоимости активов (САРМ)

Как известно, стоимость актива определяется путем дисконтирования будущих ожидаемых доходов, которые он принесет, под процентную ставку, соответствующую его риску. Модель оценки стоимости активов не дает непосредственного ответа на вопрос, какой должна быть цена актива. Однако она получила такое название, потому что позволяет определить ставку дисконтирования, используемую для расчета стоимости финансового инструмента. В модели устанавливаются следующие ограничения:

● рынок является конкурентным;

● активы ликвидны и делимы;

● отсутствуют налоги, транзакционные издержки, банкротства;

● все инвесторы имеют одинаковые ожидания, действуют рационально, стремясь максимизировать свою полезность, имеют возможность брать кредит и предоставлять средства под ставку без риска;

● рассматривается один временной период;

● доходность является только функцией риска;

● изменения цен активов не зависят от существовавших в прошлом уровней цен.

Рассмотрим, прежде всего, линию рынка капитала.

20.1.1. Линия рынка капитала (CML)

В САРМ зависимость между риском и ожидаемой доходностью можно описать с помощью линии рынка капитала (CML – Capital Market Line), которая представлена на рис. 20.1.

На графике М – это рыночный портфель, rf – актив без риска с доходностью rf ; rf L – линия рынка капитала; σm – ожидаемый риск рыночного портфеля; E(rm) – ожидаемая доходность рыночного портфеля.

Все возможные оптимальные (эффективные) портфели, т. е. портфели, которые включают в себя рыночный портфель М, расположены на линии rf L. Она проходит через две точки – rf и М. Таким образом, линия рынка капитала является касательной к эффективной границе Марковица и представляет собой не что иное как эффективную границу портфелей при возможности заимствования и кредитования. CML получила такое название именно потому, что составляющие ее портфели формируют, заимствуя средства или предоставляя кредиты под ставку без риска на рынке капитала.

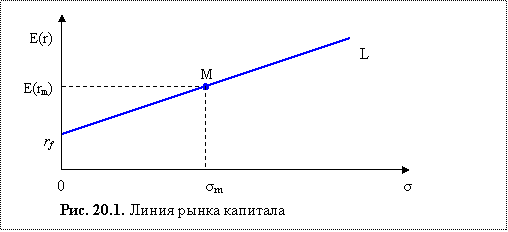
Все другие портфели, в которые не выходит рыночный портфель, располагаются ниже линии rf L. CML поднимается вверх слева направо и говорит о том, что, если портфель имеет более высокий риск, он должен иметь и более высокую ожидаемую доходность.

Соответственно, если вкладчик желает получить более высокую ожидаемую доходность, он должен согласиться на более высокий риск. Наклон CML следует рассматривать как вознаграждение в единицах ожидаемой доходности за каждую дополнительную единицу риска, которую берет на себя вкладчик.

Когда вкладчик приобретает актив без риска, он обеспечивает себе доходность на уровне ставки без риска rf. Если он стремится получить более высокую ожидаемую доходность, то он должен согласиться на некоторый риск.

Ставка без риска ( rf ) является вознаграждением за время, т. е. деньги во времени имеют ценность. Дополнительная доходность, получаемая инвестором сверх ставки без риска, есть вознаграждение за риск.

Таким образом, вознаграждение лица, инвестировавшего свои средства в рыночный портфель, складывается из ставки rf, которая является вознаграждением за время, вознаграждения за риск в размере E(rm) – rf. Другими словами, на финансовом рынке его участники уторговывают между собой цену времени и цену риска.

CML представляет собой прямую линию. Уравнение прямой можно представить следующим образом:

где а – значение ординаты в точке пересечения её с линией CML, оно соответствует ставке без риска rf:

b – угол наклона CML.

Угол наклона определяется как отношение изменения значения функции к изменению аргумента. В нашем случае (рис. 20.1) угол наклона равен:

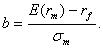
Поскольку ожидаемая доходность (у) есть функция риска (х) , то в уже принятых терминах доходности и риска уравнение CML примет вид:

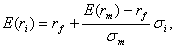
где σi – риск i-го портфеля, для которого определяется уровень ожидаемой доходности;

E(ri) – ожидаемая доходность i-го портфеля.

Данное уравнение можно записать следующим образом:

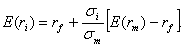(20.1)

Таким образом, ожидаемая доходность портфеля равнее ставке без риска плюс произведение отношения риска портфеля к риску рыночного портфеля и ставкой без риска.

Пример 20.1. Ставка без риска равна 10%, ожидаемая доходность рыночного портфеля 25%, риск рыночного портфеля 15%. Определить ожидаемую доходность портфеля, риск которого составляет 30%.

Решение. Ожидаемая доходность равна:

Как мы отметили выше, наклон CML следует рассматривать как вознаграждение инвестора за риск в условиях равновесия на рынке. Поэтому он является рыночной ценой риска. Таким образом, рыночная цена риска (b) равна:

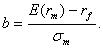
CML говорит о соотношении риска и ожидаемой доходности только для широко диверсифицированных портфелей, т. е. портфелей, включающих рыночный портфель. Но CML не отвечает на вопрос, какой ожидаемой доходностью должны обладать менее диверсифицированные портфели или отдельные активы.

20.1.2. Рыночный и нерыночный риски. Эффект диверсификации

Риск, с которым связано владение активом, можно разделить на две части.

Первая составляющая – это рыночный риск. Его также именуют не диверсифицированным, или не специфическим, или системным. Он связан с динамикой экономического цикла, общезначимыми событиями, например, войной, революцией. Когда экономика находится на подъеме, подавляющее большинство активов будет приносить более высокую доходность. Если наблюдается спад, то падает и доходность финансовых инструментов. Данный риск нельзя исключить, так как этой риск всей системы.

Вторая часть – нерыночный риск, или специфический, или диверсифицированный риск. Он связан с индивидуальными особенностями конкретного актива, а не с состоянием рынка в целом. Например, владелец акции подвергается риску потерь в связи с забастовкой на данном предприятии, некомпетентностью его руководства и т. п. Данный риск является диверсифицируемым, поскольку его можно свести практически к нулю с помощью диверсификации портфеля.

Как показали исследования западных ученых, анализировавших динамику доходности акций во второй половине 1960-х – начале 1970-х годов, портфель, состоявший из 20 активов, способен был фактически полностью исключить нерыночный риск. В случае международной диверсификации количество акций могло быть ограничено десятью. Исследования, проведенные в начале XXI века, говорят о том, что по сравнению с ми годами в 1980-е – 1990-е годы корреляция между акциями уменьшилась и возросла их волатильность, связанная с нерыночным риском. Это требует сейчас более широкой диверсификации портфеля по составу акций для достижения того же уровня риска, что и в е годы.

Широко диверсифицированный портфель заключает в себе практически только рыночный риск. Слабо диверсифицированный портфель обладает как рыночным, так и нерыночным риском. Таким образом, инвестор может снизить свой риск только до уровня рыночного, если сформирует широко диверсифицированный портфель.

Приобретая актив, вкладчик рассчитывает получить компенсацию за риск, на который он идет. Каким образом рынок будет компоненты риска с точки зрения ожидаемой доходности?

Как было сказано выше, инвестор способен практически полностью исключить специфический риск за счет формирования широко диверсифицированного портфеля. В рамках модели САРМ предполагается, что вкладчик может свободно покупать и продавать активы без дополнительных издержек. Поэтому формирование более диверсифицированного портфеля не ведет к увеличению его расходов. Таким образом, без затрат вкладчик может легко исключить специфический риск. Поэтому в теории полагается, что нерыночный риск не подлежит вознаграждению, поскольку его легко можно устранить за счет диверсификации. В связи с этим, если инвестор не диверсифицирует должным образом свой портфель, он идет на ненужный риск с точки зрения той выгоды, которую он приносит обществу.

Приобретая, например, акцию, инвестор финансирует производство и таким образом приносит обществу пользу. Покупка акции связана с рыночным риском, который является неустранимым. Поэтому инвестор должен получать вознаграждение адекватное только данному риску. В противном случае он не приобретет эту бумагу, и экономика не получит необходимые финансовые ресурсы. Однако общество (рынок) не будет вознаграждать его за специфический (не рыночный) риск, поскольку он легко устраняется диверсификацией. С точки зрения финансирования потребностей экономики данный риск не имеет смысла. Таким образом, вознаграждению подлежит только систематический (рыночный) риск. Поэтому стоимость активов должна оцениваться только относительно величины именно этого риска.

Весь риск актива (портфеля) измеряется такими показателями как дисперсия и стандартное отклонение. Для оценки рыночного риска служит другая величина, которую называют бета.

Воздействие диверсификации на риск портфеля. Как отмечалось выше, на риск портфеля основное влияние оказывает степень корреляции доходностей входящих в портфель акций – чем ниже уровень корреляции, т. е. чем ближе коэффициент корреляции приближается к (-1), тем ниже риск портфеля. Тогда можно предположить, что путем диверсификации – изменения количества входящих в портфель ценных бумаг и их характеристик – инвестор способен снизить уровень риска портфеля, не изменяя при этом его ожидаемой доходности.

Диверсификация, как процесс изменения содержимого портфеля, должна приниматься с учетом того, что варианты формирования портфеля бесконечно повторяются. Только с этим допущением можно добиться основного предназначения диверсификации – снижения риска без существенного снижения ожидаемой доходности формируемого портфеля. Действительно, если понимать диверсификацию как процесс формирования всех возможных вариантов портфелей, то мы должны прийти к выводу, что ожидаемая доходность портфеля любого объема должна в конечном итоге стремиться к ожидаемой доходности рыночного портфеля.

Чтобы доказать справедливость подобного утверждения, положим для простоты, что имеются три ценные бумаги со следующими характеристиками:

Самый простой путь оценки воздействия диверсификации на ожидаемую доходность и риск – это предположить, что все ценные бумаги имеют одинаковый вес в портфеле, т. е. W1 = W2 = W3 … = Wn = 1/n, где n – количество ценных бумаг в портфеле. Таким образом, в равновзвешенном портфеле все ценные бумаги имеют одинаковое влияние на ожидаемую доходность всего портфеля.

В рассматриваемом примере портфели формируются только из трех ценных бумаг в любом сочетании. Предположим, что инвестор принимает решение формировать портфели только из одной ценной бумаги. Чему в этом случае будет равна ожидаемая доходность таких портфелей? Отвечая на такой вопрос, необходимо учитывать, что при заданных рыночных условиях (рынок содержит только три ценные бумаги) существует три возможных портфеля, содержащих по одной ценной бумаге: а) портфель из ценной бумаги 1; б) портфель, содержащий только ценную бумагу 2; в) портфель, сформированный из ценной бумаги 3.

Тогда для первого портфеля ожидаемая доходность составит E(r1) = 0,20, у второго она будет равняться E(r2) = 0,18, а для третьего портфеля E(r3) = 0,10. Поскольку инвестор может выбрать любой из этих портфелей, то включение в портфель только одной ценной бумаги принесет инвестору в среднем ожидаемую доходность:

Предположим, что затем инвестор решил объединять в портфель две ценные бумаги. Чему будет равна в этом случае ожидаемая доходность портфеля? Существуют три возможности сформировать подобные портфели: а) портфель из ценных бумаг 1 и 2; б) портфель из ценных бумаг 1 и 3; в) портфель из ценных бумаг 2 и 3.

Поскольку по предположениям все ценные бумаги портфеля имеют равные «веса», то ожидаемые доходности портфелей составят:

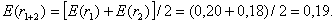
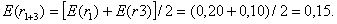
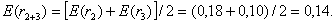
Так как инвестор может выбрать любой из этих портфелей, то в среднем ожидаемая доходность, получаемая инвестором от портфеля, сформированного из двух ценных бумаг, составит:

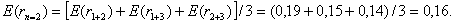
Наконец, предположим, что инвестор формирует портфель из трех ценных бумаг. По нашим предположениям, на рынке обращаются только три ценные бумаги, значит, в этом случае формируется рыночный портфель. Ожидаемая доходность такого портфеля составит:

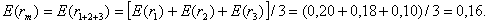
Как показывает данный пример, вне зависимости от того, какое количество ценных бумаг инвестор решил объединить в портфель, доходность, ожидаемая инвестором от любого портфеля, в среднем всегда составит 0,16. Это составляет доходность рыночного портфеля. Следовательно, диверсификация как таковая не оказывает воздействия на ожидаемую доходность портфеля. Иными словами, в среднем, вне зависимости от количества ценных бумаг в портфеле, ожидаемая доходность выбранного случайным образом портфеля всегда будет равняться ожидаемой доходности рыночного портфеля.

Однако это вовсе не означает, что все портфели заданного объема будут иметь одинаковую ожидаемую доходность. Диверсификация воздействует на дисперсию, т. е. влияет на степень отклонения ожидаемой доходности формируемых портфелей от ожидаемой доходности рыночного портфеля.

Действительно, хотя для инвестора ожидаемая доходность портфеля любого объема всегда равняется 0,16, все же при n=1 возможные варианты доходностей составляют 0,20; 0,18 и 0,10. При таком разбросе значений дисперсия составит :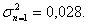

Если n=2, то варианты доходностей портфелей составляют: 0,19; 0,15 и 0,14, а дисперсия доходностей:

Наконец, при n=3 формируется единственный рыночный портфель и его дисперсия доходности

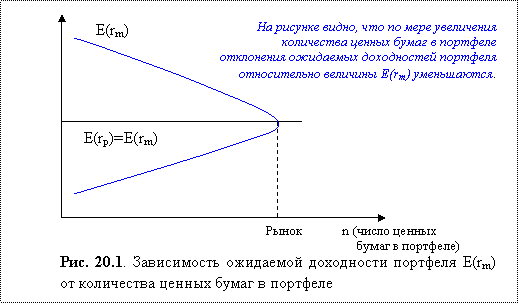
Следовательно, по мере увеличения числа ценных бумаг в портфеле дисперсия ожидаемых доходностей портфелей относительно ожидаемой доходности рыночного портфеля уменьшится, и значения E(rP) всё ближе располагаются к E(rm). Этот вывод иллюстрирует график 20.1.

Как следует из рис. 20.1, разброс ожидаемых доходностей относительно E(rm) максимален, когда n=1, и сходит на нет при формировании рыночного портфеля. Однако средняя величина такого распределения не меняется и всегда равна ожидаемой доходности рыночного портфеля. Таким образом, несмотря на то, что в среднем для инвестора ожидаемая доходность портфеля остается неизменной, имеется причина диверсифицировать портфель, поскольку в таком случае уменьшается неопределенность относительно ожидаемой доходности формируемого портфеля.

Предположим, что в портфель входит n акций. Тогда дисперсия такого портфеля вычисляется по формуле:

(7.8)

Чтобы показать зависимость риска портфеля от диверсификации, предположим для простоты, что все ценные бумаги имеют равные «веса», т. е. на каждую бумагу инвестор тратит 1/n своего начального инвестиционного капитала. Проводя соответствующие вычисления, можно показать, что в этом случае выражения для ожидаемой величины дисперсии портфеля примет вид:

(7.9)

где - ожидаемый риск портфеля из n акций;

- ожидаемая (средняя арифметическая) величина дисперсий ценных бумаг, входящих в портфель: что определяет неопределенность доходностей (риск) каждой отдельной акции портфеля.

- ожидаемая (средняя арифметическая) величина ковариаций ценных бумаг портфеля: что определяет риск взаимосвязи доходностей акций портфеля друг с другом.

Как видно из формулы (7.9), ожидаемый риск портфеля состоит из двух компонент:

1)  средней величины дисперсий ценных бумаг, входящих в портфель

2)  средней величины ковариаций ценных бумаг в портфеле

Именно такая взаимосвязь компонентов суммарного риска портфеля объясняет суть диверсификации: по мере увеличения числа n ценных бумаг в портфеле первое слагаемое в формуле (7.9) начинает уменьшаться, и риск портфеля будет приближаться к средней арифметической величине ковариаций .

Это позволяет утверждать, что если ценные бумаги портфеля не связаны абсолютной положительной корреляцией, т. е. если то часть суммарного риска портфеля может быть снижена путем диверсификации. Данная составляющая риска портфеля образует его диверсифицируемую (несистематическую) часть. В таком случае второе слагаемое характеризует систематический риск портфеля, не устранимый путем диверсификации.

Когда в портфель войдут все ценные бумаги, обращающиеся на финансовом рынке, то будет сформирован так называемый, рыночный портфель. Риск рыночного портфеля практически полностью определяется вторым слагаемым формулы (7.9), т. е. средней арифметической величиной ковариаций входящих в рыночный портфель акций.

Итак, та часть риска портфеля, которая может быть устранена путем диверсификации, называется диверсифицируемым, или несистематическим, риском. Доля же риска, которая не устраняется диверсификацией, носит название недиверсифицируемого, или систематического, риска.

Взаимосвязь между количеством ценных бумаг в портфеле (т. е. степенью диверсификации) и уровнем риска можно продемонстрировать на рис. 7.4.

Поскольку средняя величина ковариаций определяется степенью корреляции доходностей ценных бумаг портфеля, то очевидно, что чем меньше будут взаимосвязаны между собой доходности ценных бумаг (т. е. чем ближе их коэффициенты корреляций к величине – 1), тем ниже окажется риск портфеля.

Как показывают исследования, более низкие коэффициенты корреляции имеют ценные бумаги одной страны с ценными бумагами других стран. В этой связи во многих развитых странах просматривается тенденция к увеличению числа приобретаемых ценных бумаг иных государств.

Приведенная на рис. 7.4 зависимость суммарного риска портфеля от количества ценных бумаг проявляется только в том случае, если для каждой величины n перебирать все возможные варианты формирования портфеля и рассчитать среднюю величину дисперсии портфеля.

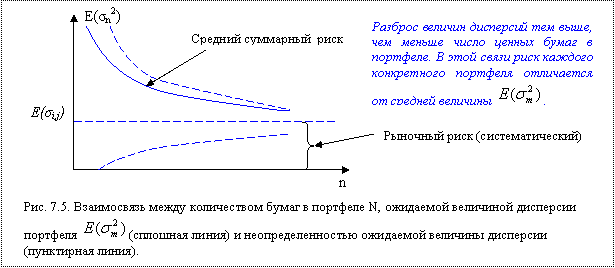
Для конкретного же портфеля его риск может отличаться от среднего значения , поскольку для выбранного портфеля любого объема всегда существует неопределенность в отношении величины риска (дисперсия портфеля). Иными словами, для любой величины N можно сформировать много портфелей, каждый из которых будет иметь свой риск (дисперсию), что отражает рис. 7.5.

20.1.3. Бета

Для измерения рыночного риска актива (портфеля) используется величина бета. Она показывает зависимость между доходностью актива (портфеля) и доходностью рынка. Доходность рынка – это доходность рыночного портфеля. Поскольку невозможно сформировать портфель, в который входили бы все финансовые активы, то в качестве него принимается какой-либо индекс с широкой базой. Поэтому доходность рынка – это доходность портфеля, представленного выбранным индексом. Бета рассчитывается по формуле:

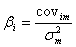
или

(20.2)

где βi – бета i-го актива;

covim – ковариация доходности i-го актива с доходностью рыночного портфеля;

corrim – ковариация доходности i-го актива с доходностью рыночного портфеля.

Поскольку величина бета определяется по отношению к рыночному портфелю, то бета самого рыночного портфеля равна единице, так как ковариация доходности рыночного портфеля с самим собой есть его дисперсия, отсюда:

где βm – бета рыночного актива.

Бета актива без риска равна нулю, потому что нулю равна ковариация доходности актива без риска с доходностью рыночного портфеля.

Величина β актива говорит о том, насколько риск актива больше или меньше риска рыночного портфеля. Активы с бетой больше единицы обладают большим риском, чем рыночный портфель, а активы с бетой меньше единицы менее рискованны, чем рыночный портфель.

Относительно величины бета активы делят на агрессивные и защитные. Бета агрессивных активов больше единицы (β > 1), а защитных – меньше единицы (β < 1). Если бета равна единице (β = 1), то риск актива равен риску рыночного портфеля.

Бета может быть как положительной, так и отрицательной величиной. Положительное значение беты говорит о том, что доходности актива и рынка при изменении конъюнктуры изменяются в одном направлении. Отрицательная бета показывает, что доходности актива и рынка меняются в противоположных направлениях. Подавляющая часть активов имеет положительную бету.

Бета актива показывает, в какой степени доходность актива (и его цена) будут реагировать на действие рыночных сил. Зная бету актива, можно оценить, насколько должна измениться его ожидаемая доходность при изменяемой доходности рынка. Например, бета бумаги равна +2. Это значит, что при увеличении ожидаемой доходности рыночного портфеля на 1% следует ожидать роста доходности бумаги на 2%. Поскольку бета бумаги больше единицы, то она рискованнее рыночного портфеля. Если бета бумаги равна 0,5, то при увеличении ожидаемой доходности рынка на 1% ожидаемая доходность бумаги должна возрасти только на 0,5%. Напротив, при снижении доходности рынка на 1% доходность бумаги уменьшится только на 0,5%. Таким образом, риск данной бумаги меньше риска рынка.

Если бета равна -2, то при повышении доходности рыночного портфеля на 1% доходность актива снизится на 2% и наоборот. Активы с отрицательной бетой являются ценными инструментами для диверсификации портфеля, поскольку в этом случае можно построить портфель с «нулевой бетой», который не будет нести риска. Здесь, однако, следует помнить, что такой портфель не аналогичен активу без риска, так как при нулевом значении беты он не будет содержать только системного риска. В то же время данный портфель сохранит риск нерыночный.

Зная величину беты для каждого из активов, вкладчик может легко сформировать портфель требуемого уровня риска и доходности. Бета портфеля – это средневзвешенное значение величин бета активов, входящих в портфель, где весами выступают их удельные веса в портфеле. Она рассчитывается по формуле:

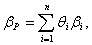
где βp – бета портфеля;

βi – бета i-го актива;

θi – удельный вес i-го актива.

Пример. Инвестор формирует портфель из трех активов: А, В и С. ΒA =0,8; ΒB =0,95; ΒC =0,2; A =0,5; θB =0,2; θC =0,3. Определить бету портфеля.

Решение. Бета равна:

Бета каждого актива рассчитывается на основе доходности актива и рынка за предыдущие периоды времени. Информацию о значениях беты можно получить от аналитических компаний, которые занимаются анализом финансового рынка.

20.1.4. Линия рынка актива (SML)

CML показывает соотношение риска и доходности для эффективных портфелей. Но она ничего не говорит о том, как будут оцениваться неэффективные портфели или отдельные активы. На этот вопрос отвечает линия рынка актива (SML – Security Market Line). SML является главным итогом CARM. Она говорит о том, что в состоянии равновесия ожидаемая доходность актива равна ставке без риска плюс вознаграждение за рыночный риск, который измеряется величиной бета. SML изображена на рис. 20.2. Она представляет собой прямую линию, проходящую через две точки, координаты которых равны rf, 0 и E( rm ), 1. Таким образом, зная ставку без риска и ожидаемую доходность каждого актива и портфеля, независимо от того, эффективный он или нет, должна располагаться на SML.

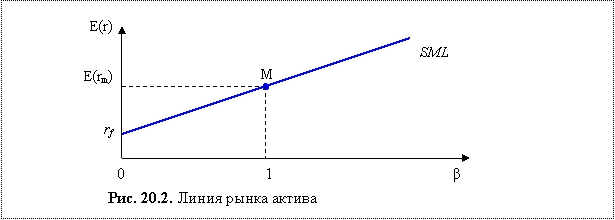
Следует еще раз подчеркнуть, что если на CML находятся только эффективные портфели, то на SML должны располагаться как широко диверсифицированные, так и неэффективные портфели и отдельные активы.

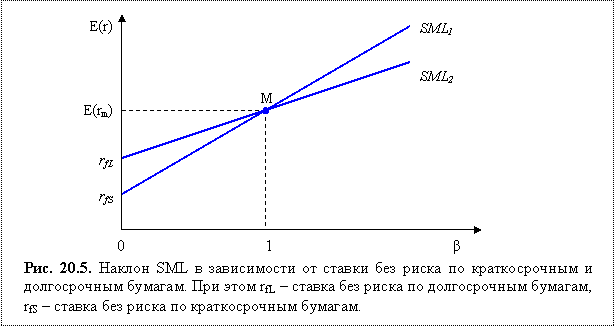
Уравнение SML имеет вид:

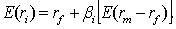. (20.3)

С его помощью можно определить ожидаемую доходность актива.

Пример. Ставка без риска равна 15%, ожидаемая доходность равна 25%. Определить ожидаемую доходность актива с бетой 1,5.

Решение. Она равна:

Наклон SML определяется отношением инвесторов к риску в различных условиях рыночной конъюнктуры.

Если у вкладчиков оптимистичные прогнозы на будущее, то наклон SML будет менее крутой, так как в условиях хорошей конъюнктуры инвесторы согласны на более высокие риски (поскольку они менее верны на их взгляд) при меньших значениях ожидаемой доходности (рис. 20.3 SML1).

Напротив, в преддверии неблагоприятной конъюнктуры SML примет более крутой наклон, так как в этом случае инвесторы в качестве компенсации потребуют более высокую ожидаемую доходность на приобретаемые активы для тех же значений риска (рис. 20.3 SML2).

Если у инвесторов меняются ожидания относительно ставки без риска, то это приведет к сдвигам SML. При увеличении rf SML сдвинется вверх, при понижении – вниз, как показано на рис. 20.4.

20.1.5. Вопросы, возникающие при построении SML

На практике возникает ряд проблем, затрудняющих ответ на вопрос, по каким данным следует строить SML. Как уже отмечалось, CAPM является моделью одного временного периода, поэтому в теории ставка без риска принимается равной ставке по краткосрочным ценным бумагам. Однако вкладчики строят инвестиционные стратегии, ориентируясь на долгосрочную перспективу. Если в качестве ставки без риска принять ставку по долгосрочным ценным бумагам, то, как правило, SLM примет более пологий наклон (рис. 20.5 – SML2), чем в случае использования ставки без риска по краткосрочным бумагам (рис. 20.5 – SLM1). На практике отмеченная проблема возникает в том случае, когда ставка без риска по долгосрочным и краткосрочным облигациям отличается в существенной степени и для активов (портфелей) с высокой или низкой бетой, поскольку для активов (портфелей) с бетой близкой к единице разница в доходности для двух случаев не будет большой.

Возникает вопрос и относительно точности прогнозирования ожидаемой доходности рынка.

20.1.6. CML и SML

Чтобы лучше понять CML и SML, сравним их характеристики. В состоянии рыночного равновесия на CML располагаются только эффективные портфели. Все прочие портфели и отдельные активы находятся под CML. CML учитывает весь риск актива (портфеля). Единицей риска выступает стандартное отклонение.

В состоянии равновесия на SML расположены все портфели, как эффективные, так и неэффективные и отдельные активы. SML учитывает только системный риск портфеля (актива). Единицей риска является величина бета. В состоянии равновесия не эффективные портфели и отдельные активы располагаются ниже CML, но лежат на SML, так как рынок оценивает только системный риск данных портфелей (активов).

На рис. 20.6а представлен эффективный портфель В, который располагается на CML. Риск портфеля равен σВ, а ожидаемая доходность – rB. На этом же рисунке представлена бумага А. Она имеет такую же ожидаемую доходность, что и портфель В, однако ее риск σА больше риска портфеля В. Так как бумага А – это отдельный актив, то она лежит ниже линии CML. Бета портфеля В и бета бумаги А равны, поэтому и портфель В и бумага А располагаются на SML в одной точке (рис. 20.6б). Так получается потому, что рынок оценивает портфели (активы) не с точки зрения их общего риска, который измеряется стандартным отклонением, а только на основе их рыночного риска, измеряемого бетой.

В результате актив А оценивается рынком точно также, как и портфель В, хотя общий риск актива А больше риска портфеля В.

CML и SML можно сравнить еще следующим образом. Подставим из формулы (20.2) значение β в формулу SML (20.3). В результате получим уравнение SML несколько в ином виде:

Формулу (20.1) для CML также можно записать аналогичным образом:

Однако в случае CML коэффициент корреляции равен +1, что говорит о полной корреляции эффективных портфелей с рынком. Не эффективные портфели и отдельные активы не имеют полной корреляции с рынком, что и нашло отражение в уравнении SML.

САРМ ничего не говорит о взаимосвязи ожидаемой доходности отдельного актива и его полного риска, измеряемого стандартным отклонением. SML устанавливает зависимость только между ожидаемой доходностью актива и его системным риском.

20.1.7. Альфа

Согласно САРМ цены активов будут изменяться до тех пор, пока каждый из них не окажется на SML, то есть пока не наступит равновесие на рынке. Поэтому на практике можно обнаружить активы, которые неверно оценены рынком относительно уровня их равновесных ожидаемых доходностей. Если эта оценка не соответствует реальному инвестиционному качеству актива, то в следующий момент рынок изменит свое мнение в направлении более объективной оценки. В результате мнение рынка будет стремиться к некоторому равновесному (т. е. верному) уровню оценки. В реальной практике периодически происходит изменение конъюнктуры рынка, что вызывает и изменение оценок в отношении ожидаемой равновесной доходности. Однако в САРМ мы рассматриваем только один временной период, поэтому и можем говорить о равновесной доходности, которая в конечном итоге должна возникнуть на рынке для данного актива. Возможные отклонения от равновесного уровня могут наблюдаться в силу каких-либо частных причин в течение коротких промежутков времени. Однако в следующие моменты должно возникнуть движение доходности актива к точке равновесного уровня.

Если актив переоценен рынком, то уровень его ожидаемой доходности ниже, чем актив с аналогичной характеристикой риска, если недооценен, то выше.

Альфой называется показатель, который говорит о величине переоценки или недооценки актива рынком. Альфа представляет собой разность между действительной ожидаемой доходностью актива и равновесной ожидаемой доходностью, т. е. доходностью, которую требует рынок для данного уровня риска.

Альфа определяется по формуле:

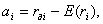
где ai – альфа i-го актива;

r∂i – действительная ожидаемая доходность i-го актива;

E(ri) равновесная ожидаемая доходность.

На рис. 20.7 представлены два актива, которые неверно оценены рынком по отношению к уровню их риска. Актив А недооценен, В – переоценен. Согласно SML ожидаемая доходность А в условиях равновесия должна составлять 12,5%, фактическая оценка – 13%, т. е. актив предлагает 0,5% дополнительной доходности, поэтому его альфа равна +0,5. Противоположная ситуация представлена для актива В. Его равновесная ожидаемая доходность согласно SML составляет 17,5%, фактически он предлагает 13%, т. е. его альфа равна

- 4,5. Таким образом, актив недооценен рынком, если его альфа положительна, и переоценен, если альфа отрицательна. Для равновесной ожидаемой доходности альфа равна нулю.

Инвесторы, которые желают получить более высокие доходы, должны стремиться приобретать активы с положительной альфой. Через некоторое время рынок заметит недооценку, и цена их повысится. Одновременно инвесторам следует продавать активы с отрицательной альфой, так как в последующем их цена понизится.

Доходность портфеля – это средневзвешенная величина доходностей входящих в него активов. Поэтому альфа портфеля также является средневзвешенной величиной и определяется по формуле:

где aр – альфа портфеля;

θi – удельный вес i-го актива в портфеле;

аi – альфа i-го актива.

Пример. Портфель состоит из трех бумаг: А, В и С. аA = 2; аB = 1,5; аC = -1; A =0,5; θB =0,2; θC =0,3. Определить альфу портфеля.

Решение. Альфа портфеля равна:

20.2. Модификации САРМ

20.2.1. САРМ для случая, когда ставки по займам и депозитам не равны

Начальная версия САРМ предполагает, что ставки по займам и депозитам одинаковы. В реальной жизни они отличаются. Напомним, что в таких условиях эффективная граница не является линейной, а представляет собой несколько отрезков, как показано на рис. 20.8.

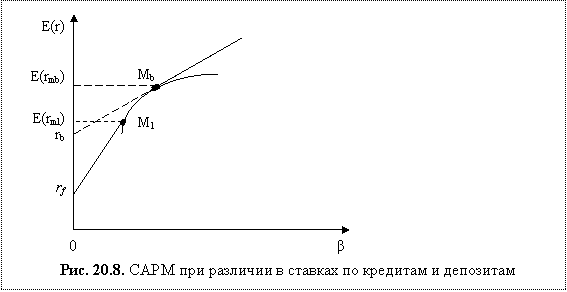
Для данного варианта возникают две формулы САРМ и SML, которые рассчитываются относительно двух рыночных портфелей в точках Ml и Mb:

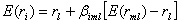
для случая, когда - кредитный портфель, и

для случая, когда - заемный портфель,

где - бета, рассчитанная портфеля Ml;

где - бета, рассчитанная портфеля Mb.

20.2.2. САРМ с нулевой бетой

Вторая модификация САРМ возникает для случая, когда отсутствуют активы без риска, но имеется актив, который содержит только нерыночный риск. Рыночный риск у него отсутствует и поэтиому его бета равна нулю. Для такой ситуации можно построить SML, который будет проходить через рыночный портфель и рискованный портфель с нулевой бетой. Уравнение САРМ в этом случае принимает вид:

где r0 – рискованный актив с нулевой бетой.

20.2.3. Версия САРМ для облигаций

Основная версия модели САРМ подходит и для облигаций. Однако для облигаций можно построить и специальную версию САРМ. Она имеет следующий вид:

(20.4)

где E(ri) – ожидаемая доходность i-ой облигации;

E(rm) – ожидаемая доходность рыночного портфеля облигаций;

βi – коэффициент бета i-й облигации. Он равен отношению дюрации облигации i(Di) к дюрации рыночного портфеля облигаций (Dm).

Формула (20.4) говорит о том, что если доходность рыночного портфеля облигаций возрастает на 1%, то доходность i-й облигации вырастает на величину βi.

На рис. 20.9 представлена линия рынка облигаций. Как следует из формулы, в данной версии САРМ доходность облигации является линейной функции дюрации облигации.

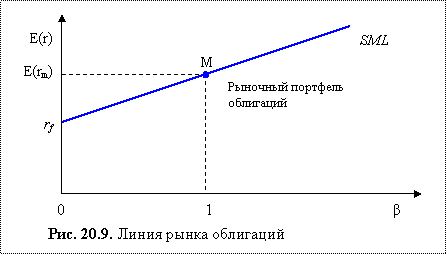
При использовании данной модели следует помнить, что она завышает доходность долгосрочных облигаций при повышении ставок. Так, для облигации с дорацией 10 лет формула дает результат, который в 10 раз больше, чем для облигации с дюрацией 1 год. На практике данная разница не столь велика.

20.2.4. Версия САРМ для фьючерсных контрактов

Чтобы получить САРМ для фьючерсов, необходимо определить, чему равна ожидаемая доходность фьючерсного контракта, если рассматривать показатель доходности аналогично общему показателю доходности, т.е. как отношение изменения цены актива к его первонакчальной цене[1]. Для рассуждений воспользуемся формулой определения фьючерсной цены для актива, по которому не выплачиваются доходы в течение действия контракта:

(20.5)

Доходность фьючерсного контракта равна отношению изменения фьючерсной цены (dF) к первоначальной цене контракта, а именно: dF/F. На основе формулы (20.5) dF можно представить следующим образом:

(20.6)

Разделим обе части равенства (20.6) на F:

(20.7)

Умножим и разделим правую часть формулы (20.7) на S:

или

или

(20.8)

Таким образом, доходность фьючерсного контракта равна доходности базового актива. Если мы возьмем математическое ожидание в формуле (20.8), то получим: ожидаемая доходность фьючерсного контракта равна ожидаемой доходности базового актива.

Обозначим ожидаемую доходность i-го фьючерсного контракта через E(rFi), т. е. E(dF/F) = E(rFi), и ожидаемую доходность i-го спотового актива через E(rSi), т. е. E(dS/S) = E(rSi). Тогда можно записать:

(20.9)

Как следует из формулы (20.9), версия САРМ для фьючерсного контракта совпадает с моделью САРМ для базисного актива, и бета фьючерсного контракта равна бете спотового актива.

20.2.5. Версия САРМ для опционов

Доходность опциона колл можно определить как отношение изменения премии опциона (dc) к первоначальной цене опциона, а именно:

(20.10)

Представим выражение (20.10) в следующем виде:

(20.11)

где S – цена базисного актива.

В выражении (20.11) dS/S = rS – это доходность базисного актива, dc/dS = Δc – дельта опциона колл[2]. Поэтому доходность контракта колл равна:

.

Сообтвественно ожидаемая доходность опционного контракта равна:

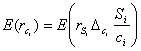
или

(20.12)

Подставив в формулу (20.12) уравнение САРМ для базисного актива, получим:

(20.13)

Из формулы (20.13) следует, что бета опциона колл (βсi) равна:

Бета опциона пут (βpi) равна:

САРМ для опциона пут составляет:

Мы рассмотрели модель САРМ. Одним из основополагающих моментов в модели выступает актив без риска. Им обычно служит государственная ценная бумага. В то же время, как свидетельствует практика, уровень доходности периодически колеблется и по данным активам. Таким образом, получается, что и они подвержены рыночному риску. В рамках же САРМ государственная ценная бумага не содержит рыночного риска. САРМ нисколько не противоречит такому положению вещей. Рассматривая бумагу без риска, необходимо не забывать, что САРМ – это модель одного временного периода. Поэтому, если инвестор приобретет бумагу без риска по некоторой цене и держит ее до погашения, то он обеспечивает себе фиксированный процент доходности, соответствующий уплаченной цене. Последующие изменения конъюнктуры и, следовательно, цены бумаги уже не влияют на доходность операции. Рыночный риск по данной бумаге возникает для инвестора только в том случае, если он решает продать ее до момента погашения.

В заключение следует сказать о результатах проверки САРМ на практике. Они показали, что эмпирическая SML или, как ее еще называют, эмпирическая линия рынка является линейной и более пологой по сравнению с теоретической SML и проходит через рыночный портфель.

Ряд исследователей подвергают САРМ сомнению. Одно из возражений заключается в том, что теоретически рыночный портфель САРМ должен включать в себя все существующие активы пропорционально их удельному весу на рынке, в том числе зарубежные активы, недвижимость, предметы искусства, человеческий капитал. Поэтому невозможно создать такой портфель на практике и в первую очередь с точки зрения определения веса активов в портфеле и оценки их доходности. Сложно оценить результаты проверки САРМ, поскольку нет определенности в отношении того, является ли выбранный для экспериментов портфель рыночным (эффективным) или нет. В целом, проверки САРМ скорее говорят о том, представляют ли портфели (индексы), используемые в тестах, эффективные портфели или нет, чем подтверждают или опровергают саму модель САРМ.

Одно из центральных мест в модели занимает коэффициент бета, оценивающий рыночный риск актива. Бета коррелирует с доходностью актива и говорит о том, что чем больше ее величина, тем больше должна быть и доходность. В то же время исследования показывают, что данная закономерность обнаруживается не всегда.

20.3. Шарпа

Ожидаемую доходность актива можно определить не только с помощью уравнения SML, но также на основе так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель была предложена У. Шарпом в середине 1960-х годов. Ее часто называют рыночной моделью[3]. В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Она предполагается линейной. Уравнение модели имеет следующий вид:

(20.14)

где E(ri) – ожидаемая доходность актива;

yi – доходность актива в отсутствии влияния на него рыночных факторов;

βi – коэффициент бета актива;

E(rm) – ожидаемая доходность рыночного портфеля;

εi – независимая случайная переменная (ошибка): показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней равно нулю. Она имеет постоянную дисперсию, ковариацию с доходностью рынка равную нулю; ковариацию с нерыночным компонентом доходности других активов равную нулю.

Если уравнение (20.14) применить к широко диверсифицированному портфелю, то значения случайных переменных εi, поскольку они изменяются как в положительном, так и в отрицательном направлениях, погасят друг друга. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь. Тогда модель Шарпа принимает вид:

где E(rp) – ожидаемая доходность портфеля;

βp – бета портфеля;

yр – доходность портфеля в отсутствии влияния рыночных факторов.

Графически модель Шарпа представлена на рис. 20.10. Она показывает зависимость между доходностью рынка (rm) и доходностью актива (ri) и представляет собой прямую линию. Ее называют линией характеристики. Независимой переменной выступает доходность рынка. Наклон линии характеристики определяется коэффициентом бета, а пересечение с осью ординат – значением показателя yi.

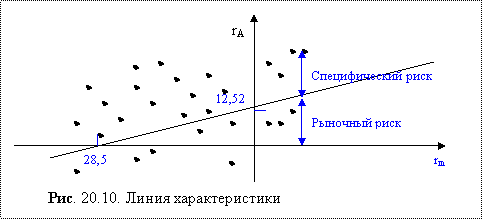
Бета рассчитывается по формуле:

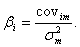
yi – определяется по формуле:

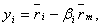
где - средняя доходность i-го актива за предыдущие периоды времени;

- средняя доходность рынка за предыдущие периоды времени.

Пример. Средняя доходность актива А равна 20%, средняя доходность рынка 17%. Ковариация доходности актива и доходности рынка составляет 0,04. Дисперсия доходности рынка 0,09. Определить уравнение рыночной модели.

Решение.

Бета актива А равна:

Уравнение рыночной модели имеет вид:

Графически оно представлено на рис. 20.10. Точками показаны значения доходности актива А и рынка для различных моментов времени в прошлом.

На рис. 20.12 представлен случай, когда бета положительна, и поэтому график рыночной модели направлен вправо вверх (положительный наклон), т. е при увеличении доходности рынка доходность актива повышается, а при понижении – падает. При отрицательном значении беты график имеет отрицательный наклон: при увеличении доходности рынка доходность актива понижается. Более крутой наклон линии говорит о высоком значении беты и большем риске актива. Менее крутой наклон – о меньшем значении беты и меньшем риске. При β = 1 доходность актива соответствует доходности рынка, за исключением случайной переменной, характеризующей специфический риск.

Если построить график модели для самого рыночного портфеля относительно рыночного портфеля, то значение у для него равно нулю, а беты +1.

20.4. Коэффициент детерминации

Рыночную модель можно использовать для того, чтобы разделить весь риск актива на диверсифицируемый и недиверсифицируемый. Графически специфический и рыночный риски представлены на рис. 20.10. Согласно модели Шарпа дисперсия актива равна:

где var – дисперсия.

Так как covεm = 0, то можно записать:

где - рыночный риск актива;

- нерыночный риск актива.

Пример. Бета актива А равна 0,44, риск рынка 0,3; риск актива 0,32. Определить рыночный и нерыночный риск актива.

Решение.

Рыночный риск, представленный дисперсией, равен:

= 0,442 ▪ 0,32 = 0,0174.

Стандартное отклонение рыночного риска составляет:

или 13,19%.

Нерыночный риск, представленный дисперсией, равен:

Стандартное отклонение нерыночного риска составляет:

или 29,16%.

Для вычисления доли дисперсии актива, которая определяется рынком, используют коэффициент детерминации (R2). Он представляет собой отношение объясняемой рынком дисперсии актива к его общей дисперсии:

(20.15)

Как уже известно:

Подставив данное значение в формулу (20.15), получим результат, который говорит о том, что коэффициент детерминации – это квадрат коэффициента корреляции:

В последнем примере R-квадрат равен 0,1699. Это означает, что изменение доходности актива А можно на 16,99% объяснять измерением доходности рынка, а на 83,01% другими факторами. Чем ближе значение R-квадрат к единице, тем в большей степени движение рынка определяет изменение доходности актива. Обычное значение R-квадрат в рыночной экономике составляет от 0,2 до 0,5, т. е. от 20 до 50% его доходности определяется рынком. R - квадрат для широко диверсифицированного портфеля может составлять 0,9 и большую величину.

20.5. САРМ и модель Шарпа

Чтобы лучше понять САРМ и модель Шарпа, проведем между ними сравнение. САРМ и модель Шарпа предполагает наличие эффективного рынка. В САРМ устанавливается зависимость между риском и доходностью актива. Независимыми переменными выступают бета (для SML) или стандартное отклонение (для CML), зависимой – доходность актива.

В модели Шарпа доходность актива зависит от доходности рынка. Независимая переменная – это доходность рынка, зависимая – доходность актива.

SML, CML и линия характеристики в модели Шарпа пересекают ось ординат в разных точках. Для SML и CML – это ставка без риска, для графика Шарпа – значение у. Между значением у в модели Шарпа и ставкой без риска можно установить следующую взаимосвязь. Запишем уравнение SML и раскроем скобки:

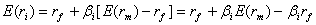
или

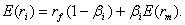
Поскольку слагаемое является общим для SLM и модели Шарпа, то:

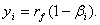(20.16)

Из уравнения (20.16) следует, что для актива с бетой равной единице у будет приблизительно равен нулю. Для актива с β <1 y>0, а для β>1 y<0. Если представить актив, для которого одновременно y>0 и β>1, это будет означать, что он в любых условиях покажет результаты лучше, чем результаты рынка. Однако такая ситуация привлекла бы повышенное внимание инвесторов, и вследствие изменения его цены установилась бы отмеченная выше закономерность.

Модель САРМ является равновесной моделью, то есть она говорит о том, каким образом в условиях эффективного рынка устанавливаются цены финансовых активов. Модель Шарпа является индексной моделью, то есть она показывает, каким образом доходность актива связана со значением рыночного индекса. Теоретически САРМ предполагает рыночный портфель, и поэтому величина β в САРМ предполагает ковариацию доходности актива со всем рынком. В индексной модели учитывается только какой-либо рыночный индекс, и бета говорит о ковариации доходности актива с доходностью рыночного индекса. Поэтому теоретически β в САРМ не равна β в модели Шарпа. Однако на практике невозможно сформировать действительно рыночный портфель и таким портфелем в САРМ также выступает некоторый рыночный портфель с широкой базой. Если в САРМ и модели Шарпа используется один и тот же рыночный индекс, то β для них будет величиной постоянной.

20.6. Определение набора эффективных портфелей

Рассматривая вопрос об эффективной границе, мы привели метод Марковитца определения набора эффективных портфелей. Неудобство его состоит в том, что для определения риска широко диверсифицированного портфеля необходимо сделать большое число расчетов. Это достигается благодаря следующим преобразованиям. Ковариация i-го и j-го активов на основе уравнения Шарапа равна:

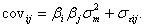(20.17)

Если i=j, то σεij = σ2i; если i≠j, то σεij = 0.

Для определения риска портфеля подставим формулу (20.17) в формулу, предложенную Марковитцем:

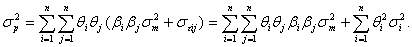(20.18)

При использовании формулы (20.18) для оценки риска портфеля следует учитывать, что экономия в вычислениях достигает за счет уменьшения точности оценки риска.

20.7. Многофакторные модели

Существуют финансовые инструменты, которые по-разному реагируют на изменение различных макроэкономических показателей. Например, доходность акций компаний, выпускающих автомобили, более чувствительна к общему состоянию экономики, а акции ссудосберегательных учреждений – к уровню процентных ставок. Поэтому в ряде случаев более точным может оказаться прогноз доходности актива на основе многофакторной модели, включающей несколько переменных, от которых зависит доходность данного актива. Выше мы представили модель Шарпа, которая является однофакторной. Ее можно превратить в многофакторную, если слагаемое представить в качестве нескольких слагаемых, каждое из которых является одной из макроэкономических переменных, определяющих доходность актива. Например, если инвестор полагает, что доходность акции зависит от двух составляющих – общего объема выпуска продукции и процентных ставок, то модель ее ожидаемой доходности примет вид:

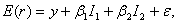
где I1 – индекс выпуска продукции;

I2 – индекс процентных ставок;

β1, β2 - коэффициенты, которые говорят о влиянии соответственно индексов I1 и I2 на доходность акции;

ε – случайная ошибка. Она показывает, что доходность бумаги может изменяться в некоторых пределах в связи со случайными обстоятельствами, т. е. независимо от принятых индексов.

& Литература

1.  , , Инвестиционное дело. М. 2010.

2.  Дж. Принципы инвестиций. М., СПб. 2002.

3.  С. Финансовый менеджмент. СПб. 2007.

4.  Н. Рынок ценных бумаг и производных финансовых инструментов. 3-е изд. М. 2009.

5.  , Финансово-денежная экономика. М.2009.

6.  Дж., Дж. Основы инвестирования. М. 1999.

7.  , , У. Финансовые институты, рынки и деньги. СПб. 2000.

8.  , Д. Финансовые институты и рынки. М. 2003.

9.  Рынок ценных бумаг. М. 2007.

10.  А. Ценные бумаги для бизнеса. М. 2006.

11.  и др. Фондовый рынок. М. 2000.

12.  Дж. Управление инвестициями. М. 2000.

[1] В данном случае речь не идет о доходности операции с фьючерсным контрактом для инвестора его инвестиций, т. е. начальной маржи.

[2] Более подробно о дельте опционов см. наш Интернет-курс «Лекции по ФПИ», параграф 10.1.

[3] Шарм предложил модель, которую назвали диагональной. После небольшой корректировки Дж. Трейнором она получила вид, представленной уравнением (20.14).