Автоматизация процессов планирования строительного производства промышленных объектов

На правах рукописи

Тарасенко Дмитрий Сергеевич

Автоматизация процессов ПЛАНИРОВАНИЯ строительного производства ПРОМЫШЛЕННЫХ ОБЪЕКТОВ

Специальность 05.13.06 – Автоматизация и управление технологическими процессами и производствами (промышленность)

Автореферат

диссертации на соискание ученой степени

кандидата технических наук

Москва - 2008

Работа выполнена в Московском автомобильно-дорожном институте (государственном техническом университете) на кафедре «Автоматизированные системы управления».

Ведущая организация: Московский государственный технический университет (МГТУ им. Баумана), г. Москва

Защита состоится «21» января 2009г. в 10 часов на заседании диссертационного совета Д.212.126.05 при Московском автомобильно-дорожном институте (государственном техническом университете) по адресу:

ГСП А-47, Москва, Ленинградский пр.,.

С диссертацией можно ознакомиться в библиотеке МАДИ (ГТУ).

Текст автореферата размещен на сайте Московского автомобильно-дорожного института (государственного технического университета): www. *****

Автореферат разослан «19» декабря 2008 г.

Отзыв на автореферат в одном экземпляре, заверенный печатью, просим направлять в адрес совета института

Общая характеристика работы

Актуальность проблемы

До сих пор не решен широкий круг вопросов, связанных с автоматизацией подготовки строительства. Возникают трудности при обработке проектно-сметной документации, формировании перспективных и годовых планов строительно-монтажных работ, организации материально-технического снабжения и комплектации строительных процессов.

Первоначально разработанные строительные планы обычно не являются лучшими по срокам выполнения работ и использованию ресурсов. Поэтому они подвергаются анализу и оптимизации. При оптимизации с привлечением дополнительных ресурсов (материальных, технических, трудовых) требуется учитывать большое количество факторов, влияющих на принятие решения. Эти задачи сложны для человека и в тоже время их нельзя доверить ЭВМ. Системы поддержки принятия решений (СППР) позволяют решать такие задачи. Они поддерживают, а не заменяют, выработку решений, предлагая специалистам возможные варианты решений и указывая на возможные последствия. С помощью СППР можно решать неструктурированные и слабоструктурированные многокритериальные задачи.

Практика показывает, что эффективное планирование и использование ресурсов, в том числе и трудовых – важнейшие факторы, оказывающие влияние на повышение темпов строительства, рост производительности труда и ввод объектов в установленные сроки. Все это и определяет актуальность выбранной темы диссертационной работы.

Цель и основные задачи исследования

Целью настоящей работы является повышение эффективности календарного планирования строительного производства промышленных объектов за счет создания автоматизированной системы для оптимизации календарных планов с привлечением дополнительных ресурсов по времени и по затратам.

Для достижения поставленной цели в работе решаются следующие задачи:

·  анализ методов, моделей и программного обеспечения применяемых для создания и оптимизации строительных планов промышленных объектов;

·  исследование методов и подходов по вероятностному планированию и управлению производственными рисками в строительных проектах;

·  формализованное представление объектов системы поддержки принятия решений для оптимизации строительных планов;

·  создание моделей и алгоритмов системы поддержки принятия решений для оптимизации строительных планов;

·  разработка программного инструментария с визуально-графическим интерфейсом для создания и оптимизации строительных планов.

Методы исследований

При разработке формальных моделей компонентов автоматизированной системы для оптимизации строительных планов в диссертации использованы методы общей теории систем, теории важности критериев, теории графов, методы оптимизации строительных процессов, имитационное моделирование, теории баз данных и др.

Научная новизна работы состоит в разработке методов, моделей и алгоритмов оптимизации строительных планов по продолжительности и по затратам с учетом стохастического характера производственного процесса, на основе которых проводится оптимизация с изменением количества привлекаемых ресурсов.

Практическая значимость работы заключается в разработке программного комплекса, используемого в технологических процессах подготовки строительства. Он позволяет создавать и оптимизировать календарные планы, а также учитывать и отслеживать производственные риски строительных проектов.

На защиту выносятся:

·  метод и алгоритм автоматического построения ускоренной сетевой модели;

·  методы вероятностного планирования и управления производственными рисками при создании строительных планов;

·  метод и алгоритм оптимизации строительных планов с использованием СППР на основе теории важности критериев;

·  программный комплекс для создания и оптимизации строительных планов.

Достоверность научных положений, рекомендаций и выводов

Обоснованность научных положений, рекомендаций и выводов определяется корректным использованием современных математических методов и моделей, согласованностью результатов аналитических и имитационных моделей. Достоверность положений и выводов диссертации подтверждена положительными результатами внедрения разработок на нескольких предприятиях.

Практическая ценность и реализация результатов работы

Научные результаты, полученные в диссертации, доведены до практического использования. Они представляют непосредственный интерес в области автоматизации процессов планирования строительного производства.

Разработанные методы и алгоритмы прошли апробацию и внедрены для практического применения на предприятиях ЗАО "СУ-7 Фундаментстрой" и ООО "Строймонолит", а также используются при организации учебного процесса на кафедре АСУ МАДИ(ГТУ).

Апробация работы

Содержание отдельных разделов и диссертации в целом было доложено и получило одобрение:

·  на международных, российских и на 64÷66 научно-методических конференциях МАДИ(ГТУ) ( г. г.);

·  на совместном заседании кафедры АПП и АСУ МАДИ(ГТУ).

Совокупность научных положений, идей и практических результатов исследований в области автоматизации процессов планирования строительного производства составляет актуальное научное направление.

Содержание работы

Структура работы соответствует списку перечисленных задач, содержит описание разработанных методов, моделей, алгоритмов и программного комплекса.

Во введении обосновывается актуальность работы, приведено краткое содержание глав диссертации, определена цель и поставлены основные задачи исследований.

В первой главе диссертации на основе исследований проведен системный анализ моделей и методов календарного планирования, которые применяют при строительстве промышленных объектов. Рассмотрены основные положения по созданию и использованию линейных календарных графиков и сетевых моделей, а также методы вероятностного планирования, такие как метод оценки и анализа программ, метод статистических испытаний или метод Монте-Карло, метод графической оценки и анализа программ.

Большая часть этой главы посвящена системному анализу методов оптимизации и коррекции проектных планов (табл. 1). Рассматриваются следующие методы:

·  метод минимизации стоимости проекта при заданной продолжительности;

·  метод условно-эквивалентной трудоемкости для оптимизации сетевой модели;

·  графический метод "время – затраты" для оптимизации сетевой модели;

·  метод сокращения сроков проекта при минимизации его общей стоимости;

·  методы приведения проекта в соответствие с ограничениями по ресурсам.

Таблица 1.

Сравнение методов оптимизации строительных планов

В этой главе рассмотрены основные принципы организации командной разработки проектной документации и программные комплексы, используемые для планирования, оценки и управления проектами (Microsoft Office Enterprise Project Management Solution и Cyco Auto Manager Team Work).

Во второй главе приведены обоснования, общие принципы и основные алгоритмы построения системы поддержки принятия решений (СППР) для оптимизации строительных планов.

Пусть множество 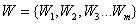– комплекс работ, выполнение которых требуется для завершения проекта. Тогда множество – будет представлять комплекс событий, возникающих в процессе выполнения комплекса работ. Сетевая модель проекта будет задаваться ориентированным графом 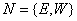, в котором элементы множества E играют роль вершин, а элементы множества W – роль дуг, соединяющих вершины, причем каждой дуге можно поставить в однозначное соответствие пару вершин и , первая из которых будет определять момент начала работы , а вторая – момент окончания этой работы.

Каждая работа в свою очередь определяется следующим множеством:

,

где – набор материалов, – затраты, – набор исполнителей, – трудоемкость, – набор используемой техники, 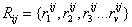– набор рисков.

Затраты на проект , включают в себя, как прямые затраты, являющиеся суммой затрат на каждую работу, так и косвенные затраты , вычисляемые исходя из продолжительности проекта:

, (1)

где Т – продолжительность проекта.

Затраты на каждую работу включают в себя стоимость материалов, использования техники и оплату труда исполнителей:

, (2)

где - стоимость материалов работы i-j, - затраты на оплату труда исполнителям работы i-j, - стоимость использования техники в работе i-j.

Продолжительность работ проекта можно регулировать количеством ресурсов, выделяемых для их выполнения. Продолжительность работы соответствующая нормальному времени выполнения работы и ее минимальной стоимости – называется нормальной продолжительностью. Продолжительность работы соответствующая ускоренному до предела времени выполнения работы – называется сжатой, или укоренной продолжительностью. Стоимость выполнения работы в такие сроки максимальна.

Время выполнения работы прямо пропорционально ее объему и обратно пропорционально числу исполнителей и используемой техники , занятых на данной работе. Так как время выполнения работы зависит от задействованных ресурсов, то можно допустить, что стоимость работы в общем случае представляет собой функцию нелинейного вида, как показано на рис. 1.

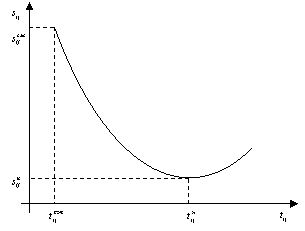
Рис. 1. График зависимости продолжительности работы от ее стоимости

Для оптимизации проекта по продолжительности и по затратам целесообразно использовать теорию важности критериев. Математическая модель ситуации принятия решения при многих критериях включает в себя три элемента: множество вариантов V, векторный критерий C и отношения предпочтения и безразличия лица принимающего решения – ЛПР, которые обозначают P (от англ. Preference – предпочтение) и I (от англ. Indifference – безразличие).

Каждый вариант v из множества всех вариантов V характеризуется значениями критериев S – стоимости и T – продолжительности проекта, которые называются частными и которые составляют векторный критерий . Под критериями S и T понимаются функции, определенные на V и принимающие значения из множества , называемого шкалой, а также множеством оценок, градаций этих критериев.

Множество вариантов представляет собой область возможных затрат и сроков выполнения проектов, как показано на рис. 2. Эти варианты отличаются различными затратами трудовых, технических и материальных ресурсов. Сузить количество вариантов, можно отбрасывая доминируемые альтернативы по Эджворту-Парето.

Рис. 2. График области возможных затрат на выполнение проекта

Альтернатива v' из множества альтернатив V называется недоминируемой или оптимальной по Эджворту-Парето, если в V не существует такой альтернативы v, для которой и , причем, хотя бы одно из этих неравенств строгое. Очевидно, что в решаемой задаче оптимальные по Эджворту-Парето решения лежат на кривой DC (рис. 2), т. е. линии минимальных затрат.

Стоимость и продолжительность проекта неоднородны, поэтому их следует привести к качественной, порядковой шкале. Для приведения стоимости и времени выполнения проекта к порядковой шкале «разрежем» исходные шкалы этих критериев на x частей, так чтобы любые значения этих критериев из части номер i имели интерпретацию по предпочтительности, соответствующие градации i общей шкалы. В качестве крайних значений шкалы возьмем значения продолжительности и стоимости проекта в точках D и C, т. е. при нормальной и при ускоренной продолжительности, причем так, чтобы большее значение x было предпочтительней (быстрее или дешевле) меньшего. Полученный интервал разделим на x частей (рис. 3).

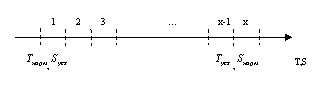
Рис. 3. Построение порядковой шкалы стоимости и продолжительности

Оценки относительной важности критериев могут быть качественными и количественными. Качественными (нечисловыми) оценками важности являются суждения (утверждения, сообщения) вида что «один критерий важнее другого» и «оба критерия равноважны». Количественными оценками важности являются суждения вида что «один критерий важнее другого во столько-то раз». Для получения от лица принимающего решения (или эксперта) качественной информации о важности критериев ему необходимо предложить попарно сравнить критерии по важности. Для каждой выбранной пары критериев ЛПР должно указать, что один из критериев более важен, чем другой, или, что они равноважны.

Для сравнения по важности критериев, т. е. стоимости и продолжительности, можно исходить непосредственно из определений равенства и превосходства в важности и сопоставлять по предпочтению пары векторных оценок вида и , где под и подразумеваются значения из интервала соответствующего i-ому значению шкалы, а под и из j-го интервала.

·  Критерии T и S равноважны, или одинаково важны, когда любые две векторные оценк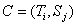и и 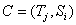одинаковы по предпочтению.

·  Критерий T важнее критерия S, когда всякая векторная оценка , в которой , предпочтительнее, чем .

Для сравнения по важности ЛПР предлагается сравнить векторные оценки и . Для повышения надежности получаемой от ЛПР информации для сравнения ему предлагается несколько пар оценок. Для повышения контрастности рекомендуется использовать крайние значения шкалы.

В некоторых случаях критерии могут оказаться несравнимыми по важности. Причин такого положения может быть несколько. Одна из них состоит в том, что данные определения носят по существу характер «глобальной» важности, т. е. охватывающей все множество векторных оценок. Однако бывают ситуации, когда в одной части этого множества, один критерий важнее другого, а в другой наоборот. В таких случаях корректируются исходные определения, ограничивая их «действие» лишь некоторой областью из множества векторных оценок, что будет соответствовать «локальной» важности.

Комбинируя полученные значения о важности критериев и отношения Эджворта-Парето можно сравнивать по предпочтению вычисляемые векторные оценки. Например, шкала имеет 5 градаций, и мы получили две векторные оценки стоимости и времени (5,3) и (2,4). Первый критерий обозначает время выполнения проекта, а второй его стоимость. От пользователя мы получили информацию, что время важнее стоимости, т. е. первый критерий важнее второго, обозначим ее . Понятно, что для этих векторных оценок неверно 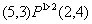ни , ни 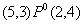(т. е. по Эджворту-Парето). Однако, можно составить цепочку из двух звеньев верных отношений . Следовательно, можно утверждать, что векторная оценка (5,3) предпочтительней, чем (2,4), т. е. .

Вариант v' такой, для которого не существует варианта v, лучшего по отношению , т. е. для которого было бы верно , называется недоминируемым по . В противном случае он является доминируемым.

После отбора вариантов на основании качественных данных многие варианты могут оказаться несравнимыми. Тогда следует получить у ЛПР дополнительную информацию о важности критериев, т. е. количественную. Количественная важность может выступать в двух основных формах:

·  степенях превосходства в важности одних критериев над другими: «критерий T в d раз важнее критерия S», где d>0, если d<1, то фактически критерий S в раз важнее критерия T, а при d=1 критерии равноважны;

·  значениях важности отдельных критериев, количественно «измеряемой» по общей для них «шкале важности»: «важность критерия T имеет величину , а важность критерия S – », где и .

Между обоими указанными видами количественной важности имеется тесная взаимосвязь. Степень превосходства d критерия T над критерием S равна отношению значений их важности и :

. (3)

Под N-моделью понимается модель с 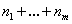однородными критериями, причем первые критериев получают повторением («клонированием») первого критерия раз, следующие критериев получают повторением второго критерия раз и т. д.

Критерий T в d раз важнее критерия S, когда для N-модели, соответствующей исходной модели, выполнены следующие условия:

; (4)

Каждый из критериев, полученный из критерия T, равноважен любому из критериев, полученному из критерия S.

В поставленной двухкритериальной задаче применение методов выбора оптимального решения с использованием информации о количественной важности не поможет отбросить спорные решения, но эта информация потребуется для совершенствования шкалы. Совершенствовать шкалу можно выясняя характер изменения предпочтений вдоль шкалы. Например, имеет место случай замедления роста предпочтений вдоль шкалы, т. е. переход от 1 к 2 важнее, чем переход от 2 к 3, который в свою очередь больше, чем переход от 3 к 4 и так далее в пределах количества градаций шкалы x.

Если критерии T и S равноважны, то это означает, что векторная оценка 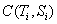, где и значения из интервала соответствующего i-ому значению шкалы, предпочтительнее, чем векторная оценка, получаемая из заменой на и на , где целое число.

Рассмотрим пример, где шкала состоит из 5 частей, и требуется сравнить две векторные оценки стоимости и продолжительности (2,3) и (3,1). От ЛПР получена информация 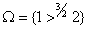и 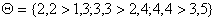. Перепишем векторные оценки в виде N=(3,2) модели и упорядочим по невозрастанию: (3,3,2,2,2) и (3,3,3,1,1). Теперь с учетом равноважности всех критериев можно составить цепочку: . Следовательно, вариант (2,3) предпочтительнее варианта (3,1).

Алгоритм оптимизации сетевой модели приведен на рис. 4. Исходными данными для алгоритма оптимизации являются две готовые сетевые модели одного проекта с нормальной и ускоренной продолжительностью. На первом этапе оптимизации строится шкала. Дальше нормальная модель постепенно ускоряется с помощью привлечения дополнительных ресурсов на основании распределения ресурсов в ускоренной модели.

На каждом шаге ускорения нормальной модели из числа критических работ выбирают такую работу, которая может дать максимальное сокращение критического пути. Если таких работ несколько, то выбирают ту из них, которая имеет наименьший коэффициент обратной пропорциональности. Значения, попадающие в интервалы шкалы, фиксируются для дальнейшего сравнения по предпочтению.

Затем пользователь опрашивается для получения информации о предпочтениях ЛПР. На основании данных опроса о предпочтениях выбираются эффективные решения. Если эффективных решений оказалось несколько, то для выбора оптимального из них опрашивается пользователь. Найденное оптимальное решение представляет собой интервалы продолжительности и стоимости, которые являются оптимальными с точки зрения ЛПР.

Найденные интервалы принимаются за оптимальные диапазоны значений и делятся на более мелкие интервалы для дальнейшей оптимизации по описанной схеме. Так продолжается до нахождения решения с требуемой точностью, которая задается в настройках системы.

Система может автоматически построить ускоренную сетевую модель на основе ранее созданной нормальной модели. Для этого используются следующие базы данных:

·  номенклатуры строительно-монтажных работ;

·  применения технических ресурсов по видам работ;

·  применения трудовых ресурсов по видам работ;

·  применения материалов по видам работ;

·  прецедентов планирования работ в предыдущих моделях.

Система автоматического построения ускоренной сетевой модели получает на вход сетевую модель с нормальной продолжительностью работ. Она проводит предварительный расчет модели и определяет работы критического пути.

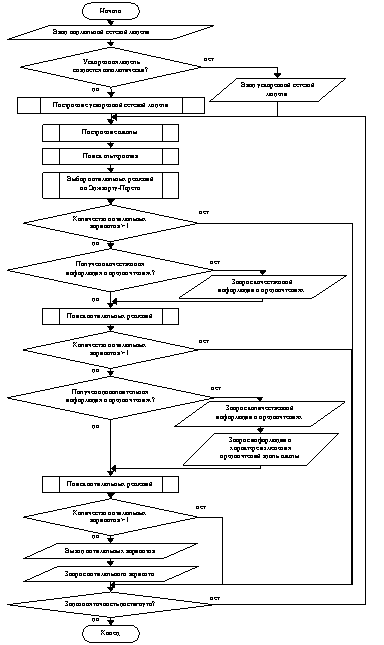
Рис. 4. Блок схема алгоритма оптимизации на основе теории важности критериев

Затем для каждой работы критического пути создается ее вариант со сжатой продолжительностью. Для этого к работе выделяется дополнительная техника и рабочие согласно ее номенклатуре. Верхняя граница количества задействованной техники и рабочих для каждого вида работ вычисляется по следующему алгоритму:

·  выбираются работы, требуемого типа, с коэффициентом напряженности близким к единице на ранее созданных ускоренных моделях;

·  по каждому виду техники и рабочей специальности рассчитывается среднее количество ресурсов на единицу объема;

·  полученное среднее количество ресурсов умножается на требуемый объем работ, и округляется таким образом, чтобы время выполнения работы было кратно половине смены.

Если прецедентов в базе данных не обнаружено, то используется величина кратная половине рабочей смены, таким образом, максимальное количество ресурсов выделенных на каждую работу позволит выполнить ее в течение половины смены. При известных пропорциях эта величина может быть задана для каждого вида работ вручную.

После этого для каждой ускоряемой работы рассчитывается коэффициент обратной пропорциональности. Выбирается работа с наибольшим коэффициентом. Если ресурсы проекта позволяют, то выбранная работа ускоряется, если нет, то берется другой ресурс или работа со следующим по величине коэффициентом обратной пропорциональности. После чего, если критический путь изменился, то модель пересчитывается для выбора новых критических работ, в противном случае ускоряется следующая работа с наибольшим коэффициентом обратной пропорциональности. Схема алгоритма приведена на рис. 5.

В третьей главе диссертации предложен метод учета стохастического характера производственных процессов строительного производства с помощь вероятностных сетевых методов. Предложена интеграция системы управления производственными и экономическими рисками в автоматизированную систему оптимизации строительных планов. Предложен метод классификации объектов, использованный в хранилище данных предприятия для работ и производственных рисков.

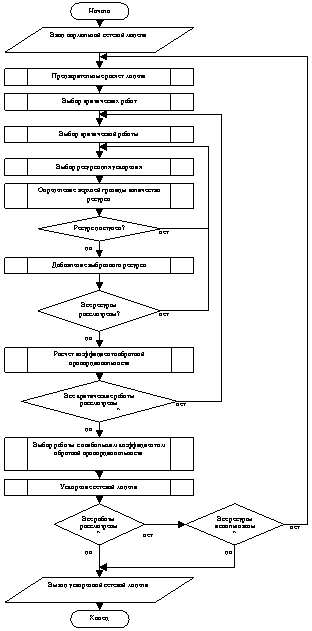
Рис. 5. Блок схема алгоритма автоматического построения ускоренной модели

В теории принятия решений выделяют две стохастические модели:

·  принятие решения в условиях неопределенности - ЛПР не знает вероятностей наступления рисковых событий;

·  принятие решения в условиях риска - ЛПР знает или предполагает вероятности наступления рисковых событий.

В  случаях, когда время выполнения и стоимость работ, а также вероятности наступления рисковых событий неопределенны, используют метод планирования работ на основании логической системы процесса, который называют методом оценки и анализа программ (Program Evaluation and Review Technique, PERT). Он позволяет определить вероятности окончания проекта в заданные периоды времени и к заданным срокам с заданной стоимостью.

Вместо единственных детерминированных величин продолжительности и стоимости, для работ проекта задают (как правило, экспертным путем) три оценки продолжительности и стоимости: оптимистические (работа не может быть выполнена быстрее, чем за и дешевле, чем за ); пессимистические (работа не может быть выполнена медленнее, чем за и дороже, чем за ) и наиболее вероятные и . Затем вероятностную сетевую модель превращают в детерминированную, на основании предположения, что продолжительность и стоимость выполнения работы имеет нормальное распределение и подчинена β-закону. Выполняют это путем замены трех оценок продолжительности и стоимости каждой из работ единственными величинами, называемыми ожидаемой продолжительностью и ожидаемой стоимостью . Они рассчитываются, как средневзвешенное арифметическое трех экспертных оценок длительности и стоимости данной работы:

 , (5)

где – математическое ожидание продолжительности работы i-j,

, (6)

где – математическое ожидание стоимости работы i-j.

Величины и представляют собой математические ожидания случайных величин продолжительности и стоимости работ. Для характеристики степени неопределенности оценок продолжительности и стоимости отдельной работы служат дисперсии, вычисляемые по формулам:

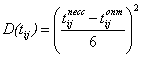, (7)

где – дисперсия продолжительности работы i-j,

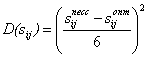, (8)

где – дисперсия стоимости работы i-j.

Этот метод имеет огромное количество недостатков и допущений, но он может использоваться в тех случаях, когда отсутствует информация о рисках, связанных с выбранной работой. В большинстве же случаев риски могут быть более или менее точно определены. Существует два метода определения вероятности наступления рискового события:

·  объективный метод определения вероятности основан на вычислении частоты, с которой происходят рисковые события, например, аварии, частота при этом рассчитывается на основе фактических данных;

·  субъективный метод, когда вероятность является предположением относительно определенного результата, основывающемся на суждении или личном опыте оценивающего, а не на частоте, с которой подобный результат был получен в аналогичных условиях.

Каждая работа будет иметь свой набор рисковых событий , независимо от метода определения рисков. В свою очередь каждое рисковое событие определяется следующими величинами:

,

где – время, которое может быть потеряно при возникновении рискового события , – сумма, которая может быть потеряна при возникновении рискового события , – вероятность наступления риска .

На основании этих данных рассчитывают математическое ожидание времени выполнения и стоимости работы. Математическое ожидание – это средневзвешенное всех возможных вариантов, где в качестве весов используют вероятности их достижения:

, (9)

. (10)

Отклонение от математического ожидания определяется дисперсией времени выполнения и стоимости работы. Дисперсия – это средневзвешенное квадратов отклонений случайной величины от ее математического ожидания:

, (11)

. (12)

После получения этих величин стоимость и продолжительность всего проекта можно рассчитать на сетевой модели уже с помощью детерминированных методов. Однако продолжительность и стоимость проекта будут иметь две оценки – ожидаемую и погрешность. Ожидаемая продолжительность критического пути равна сумме ожидаемых продолжительностей критических работ, а погрешность продолжительности критического пути равна сумме дисперсий критических работ:

, (13)

, (14)

где – работа i-j критического пути, – среднеквадратичное отклонение от ожидаемой продолжительности проекта. В данном случае при расчете продолжительности проекта придется учитывать помимо критического еще и околокритические пути, т. е. те пути, которые могут стать критическими при определенной вероятности.

Ожидаемые прямые затраты на проект будут равны сумме ожидаемых стоимостей работ, а погрешность будет равна сумме дисперсий. Общая ожидаемая стоимость проекта будет равна сумме ожидаемых прямых затрат и косвенных затрат, определенных по ожидаемой продолжительности проекта. Погрешность стоимости проекта будет рассчитываться, как сумма ожидаемой погрешности прямых и косвенных затрат:

, (15)

. (16)

где – ожидаемые косвенные затраты на проект, 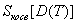– дисперсия косвенных затрат, – среднеквадратичное отклонение от ожидаемой стоимости проекта.

Наиболее близка к реальному распределению времени и стоимости проекта функция нормального распределения. Поэтому для определения вероятности реализации проекта за время и стоимость, отличные от ожидаемых, рассматривают величину стандартного (среднеквадратического) отклонения кривой нормального распределения, которая отражает степень неопределенности оценки продолжительности всего проекта:

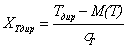, (17)

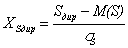, (18)

где и – аргументы функции Лапласа, т. е. 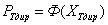– вероятность завершения проекта за директивное время и – вероятность завершения проекта с директивными затратами . Кроме того можно решить обратную задачу и определить время и стоимость проекта, которые можно получить с заданной вероятностью:

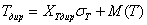, (19)

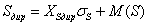. (20)

Для получения вероятностей по аргументам функции Лапласа:

, (21)

где , – математическое ожидание, а – среднеквадратичное отклонение величины , обычно используют рассчитанные табличные значения.

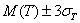Согласно теории вероятности, вероятность выполнения проекта в пределах или равна 68,27 %, а вероятность выполнения проекта в пределах или 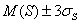равна 99,73 %, т. е. практически стопроцентная вероятность.

В четвертой главе построена имитационная модель для проверки эффективности предложенных методов. Разработана концептуальная схема данных для автоматизации построения сетевых моделей и пользовательский интерфейс программного комплекса для создания и оптимизации строительных планов. Предложена реализация программного комплекса для создания и оптимизации планов строительных работ. Приведена функциональная схема и описано функционирование реализованного программного комплекса.

Для апробации предложенных методов и алгоритмов, а также изучения процессов, направленных на оптимизацию строительных процессов, была построена модель оптимизации неритмичного потока с непрерывным использованием ресурсов (рис. 6). В качестве среды для построения модели выбрана платформа Matlab с пакетом Simulink.

Использование этой модели показало, что прежде, чем проводить оптимизацию с привлечением дополнительных ресурсов целесообразно провести оптимизацию за счет совмещения технологических процессов во времени и изменении очередности работ. Эти методы хорошо изучены и дают хорошие результаты по оптимизации, но в то же время довольно трудоемки для реализации их без использования ЭВМ.

Также в четвертой главе предложена реализация программного комплекса для создания и оптимизации строительных планов. В данном случае оптимальным является его интегрирование с системой разработки строительной документации и планирования. Это дает возможность органично вобрать данные обо всех этапах проектирования, как текущего проекта, так и остальных проектов предприятия. Такое построение системы позволяет быстрее наполнить базы данных информацией о ресурсах предприятия, что ведет к повышению эффективности системы в целом. Программный комплекс предусматривает коллективную разработку проектов, что повышает эффективность организации работы проектного отдела. Он построен на основе модулей, что обеспечивает его гибкость и расширяемость.

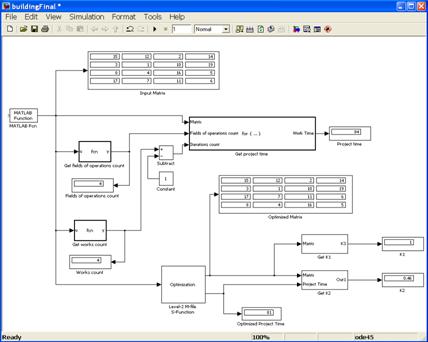
Рис. 6. Имитационная модель оптимизации неритмичного потока с непрерывным использованием ресурсов

В этой главе разработан пользовательский интерфейс программного комплекса для создания и оптимизации планов строительных работ и его основные функции. Пользовательский интерфейс предоставляет удобный доступ к функциям и базам данных системы. Главное окно приложения приведено на рис. 7. Оптимизация сетевых моделей реализована в виде мастера оптимизации, где пользователь постепенно опрашивается о предпочтениях и на основе его ответов строится оптимизированная модель. Сбор информации системой аналогичен составлению подробных технологических карт, описывающих производство отдельных работ. Технологические карты являются основной состав­ляющей частью проекта производства работ и должны быть хорошо известны потенциальным пользователям. Везде где это возможно система будет предлагать пользователю только актуальные данные для выбора: работ, техники, исполнителей, материалов, рисков. Все это сокращает время обучения персонала работе с системой, упрощает разработку сетевых моделей и повышает удобство использования системы.

Рис. 7. Основное окно системы

В заключении диссертации представлены выводы и основные результаты работы.

Приложение диссертации содержит документы об использовании результатов работы.

Публикации. По результатам выполненных исследований опубликовано 5 печатных работ, которые приведены в списке публикаций.

Основные выводы и результаты работы

1.  Проведен анализ моделей и методов представления и оптимизации строительных планов.

2.  Проведен анализ программного обеспечения, применяемого при планировании и управлении строительными процессами.

3.  Предложены модели, методы и алгоритмы, позволяющие реализовать автоматизированную систему для оптимизации строительных планов.

4.  Разработан метод автоматического построения ускоренной сетевой модели.

5.  Предложен метод построения вероятностной сетевой модели для учета стохастического характера производственных процессов.

6.  Предложен метод классификации информации для системы управления рисками.

7.  Проведена апробация предложенных методов оптимизации строительных планов с помощью имитационной модели.

8.  Разработан программный комплекс для создания и оптимизации строительных планов.

9.  Разработанный программный комплекс прошел апробацию и внедрен для практического применения на предприятиях ЗАО "СУ-7 Фундаментстрой", ООО "Строймонолит".

Публикации по теме диссертационной работы

1.  , , Снеткова формирования графиков производства строительных работ // Приборы и системы. Управление, контроль, диагностика. – М., «Научтехлитиздат», №6, 2007. С. 12-16.

2.  , , Савич генерирования комбинаций объектов при решении задачи моделирования строительного производства // Цивилизация знаний: инновацинный переход к обществу высоких технологий. Труды 9 международной научной конференции, Москва 25-26 апреля 2008 г.: в 2 ч., ч. 1. – М.: РосНОУ, 2008. С. 204-209.

3.  , Остроух задачи сравнения документов при коллективной разработке проектной документации на строительном предприятии // Вестник Российского нового университета. Выпуск 2. Серия естествознание, математика, информатика. – М.: РосНОУ, 2007, С. 112-115.

4.  , К вопросу автоматизации расчета графиков производства строительных работ // Вестник Российского нового университета. Выпуск 2. Серия естествознание, математика, информатика. – М.: РосНОУ, 2007, C. 121-124.

5.  Tarasenko D. S., Ostroukh A. V., Podporin D. I., Surkova N. E. Workflow automatization in preparation for building // Information and Telecommunication Technologies in Intelligent Systems. Proceeding of Fourth International Conference in Catalina, Italy, May 27 - June 03, 2006, P.102-104.