ФМЭ, магистратура, уч. г. Микроэкономика, адапт. курс
__________________________________________________________________________
Семинар №5
Тема: Теория поведения потребителя. Уравнение Слуцкого.(В. гл.8)
Задача 1.
Функция полезности потребителя задана формулой ![]() .
.
а) Найдите функцию спроса и функцию компенсированного спроса потребителя на 1-ое благо.
б) Найдите разложение величины ![]() на эффекты замещения и дохода.
на эффекты замещения и дохода.
Задача 2.
Агент тратит весь свой доход, равный $100, на два товара. Предпочтения данного агента представимы функцией полезности вида 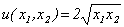 . Цены товаров заданы вектором
. Цены товаров заданы вектором ![]() .
.
А) Найдите, как изменится спрос на каждый товар, если цена первого товара увеличится до ![]() ? Изобразите полученный ответ графически.
? Изобразите полученный ответ графически.
Б) Разложите найденное изменение в потреблении первого товара на две составляющие: изменение в потреблении, вызванное эффектом дохода, и изменение в потреблении, вызванное эффектом замещения, рассчитывая эффект замещения по Слуцкому. Проиллюстрируйте графически.
В) Разложите найденное изменение в потреблении первого товара на две составляющие: изменение в потреблении, вызванное эффектом дохода, и изменение в потреблении, вызванное эффектом замещения, рассчитывая эффект замещения по Хиксу. Проиллюстрируйте графически. Сопоставьте с результатом, полученным для декомпозиции с компенсацией по Слуцкому.
Задача 3.
Рассмотрите потребителя, предпочтения которого представимы функцией полезности ![]() , имеющего доход
, имеющего доход ![]() . Пусть цены благ заданы вектором
. Пусть цены благ заданы вектором ![]() . Предположим цена первого блага увеличилась до
. Предположим цена первого блага увеличилась до ![]() . Разложите изменение спроса на первое благо на эффект дохода и эффект замещения по Слуцкому и по Хиксу. Приведите графическую иллюстрацию.
. Разложите изменение спроса на первое благо на эффект дохода и эффект замещения по Слуцкому и по Хиксу. Приведите графическую иллюстрацию.
Задача 4.
Выполните задания задачи 3 для функций
(1) ![]() ;
;
(2) ![]() .
.
Тема: Предложение труда (В. гл.9)
Задача 1.
Объясните, почему повышение ставки заработной платы может привести к падению рабочего времени, в то время как такое же повышение оплаты труда за сверхурочные работы, предложенное тому же работнику, приводит к росту рабочего времени.
Задача 2.
Рассмотрим индивидуума, который имеет два источника дохода: он получает государственную пенсию величиной ![]() и, кроме того, он может подрабатывать на госпредприятии, получая заработную плату
и, кроме того, он может подрабатывать на госпредприятии, получая заработную плату ![]() $ в час. Считайте, что предпочтения потребителя представимы функцией полезности
$ в час. Считайте, что предпочтения потребителя представимы функцией полезности ![]() с гладкими кривыми безразличия, где
с гладкими кривыми безразличия, где ![]() - потребление,
- потребление, ![]() - свободное время, нейтральное к доходу. Известно, что в этих условиях индивидуум предпочел работать
- свободное время, нейтральное к доходу. Известно, что в этих условиях индивидуум предпочел работать ![]() часов в неделю, а его потребление составило
часов в неделю, а его потребление составило ![]() единиц в месяц.
единиц в месяц.
Правительство предлагает индивиду выбрать оду из двух программ: 1 - поднять ставку заработной платы на 10%, 2 - увеличить пенсию на 20%. Побудят ли эти программы к увеличению его рабочего времени? Какую из программ выберет индивид?
Задача 3.
Пусть функция полезности индивида имеет вид: ![]() , где
, где ![]() - расходы на потребление,
- расходы на потребление, 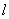 - часы досуга в течении дня. Предположим, индивид должен распределить 12 часов в день между работой и досугом. Пусть потребитель имеет также нетрудовой доход, равный 20 д. е. в день.
- часы досуга в течении дня. Предположим, индивид должен распределить 12 часов в день между работой и досугом. Пусть потребитель имеет также нетрудовой доход, равный 20 д. е. в день.
а) Если почасовая ставка зарплаты равна 10 д. е., то сколько часов индивид предпочтет работать?
б) Предположим, введен 20%-ный налог на весь доход, получаемый индивидом. Сколько часов будет работать индивид?
в) Как изменится ваш ответ на пункт (б), если налогом облагается только трудовой доход индивида? Можно ли ответить на этот вопрос, не производя дополнительных вычислений?



