Деньги в модели с перекрывающимися поколениями

Деньги в модели с перекрывающимися поколениями.

Основные функции денег:

1) Средство осуществление расчетов

2) Средство уменьшение транзакционных издержек

3) Средство сохранение и передача ценности во времени (средство совершения протяженных во времени транзакций)

В рамках модели с перекрывающимися поколениями будем рассматривать третью функцию денег.

Определение

1.  Нейтральность денег означает, что изменение денежной массы в экономике не влияет на реальные экономические переменные. То есть изменение денежной массы влечет пропорциональное увеличение цен, но реальные переменные остаются теми же самыми.

2.  Говорят, что деньги супернейтральны, если изменение темпов роста денежной массы не влияет на реальные переменные. Надо иметь в виду, что в одной и той же экономике деньги могут быть супернейтральны или не супернейтральны в зависимости от способа вливания новых денег в экономику.

§ 1. Постановка задачи и анализ решения

Рассмотрим очень простую версию модели с перекрывающимися поколениями. В этой модели сепарабельность функции полезности не существенна. Функция полезности репрезентативного потребителя может зависеть от и 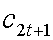довольно произвольным образом. Поэтому запишем задачу потребителя в общем виде:

(1.1)

Будем рассматривать экономику без производства. В момент своего рождения каждый потребитель получает единицу товара. Он частично тратит эту единицу товара, частично продает за деньги живущему в этом же периоде старшему поколению и сберегает вырученные от продажи деньги для того, чтобы можно было купить товар в следующем периоде. Агенты хранят деньги в «кармане», производства нет, поэтому процент по вкладам в «кармане» индивид не получает.

Таким образом, номинальное бюджетное ограничение агента, родившегося в начале «момента» , в первом периоде жизни можно записать в следующем виде:

, (1.2)

где - деньги, вырученные от продажи, которые агент несет с собой во второй период.

Во второй период жизни агента действуют цены, равные , поэтому его потребление будет определяться следующим бюджетным ограничением:

(1.3)

Материальный баланс в равновесии имеет вид:

(1.4)

В начальный момент времени задано и имеется один представитель пожилого поколения, который выбирает свое потребление в первый момент времени следующим образом:

= (1.5)

Определение

Равновесие — это набор траекторий 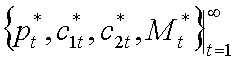таких, что

1.  Агенты ведут себя рационально при ценах , то есть 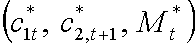являются решением задачи (1.1)-(1.3) при ценах

2.  Выполнен баланс на рынке продукта (1.4)

при заданных начальных условиях (1.5)

Отметим, что не имеет смысла рассматривать эту модель на конечном временном интервале. В этом можно убедиться, если рассматривать экономику с конца. Последнему поколению нет смысла оставлять деньги, т. к. оно знает, что до старости не доживет. Тогда и предпоследнее поколение не будет держать деньги, т. к. если последнее поколение не хочет денег, то ничего нельзя купить у них. Следовательно, все надо потреблять сейчас. И так, двигаясь к началу, мы получим, что каждое поколение не захочет иметь деньги. Но так как в начальный момент они есть, то равновесия с положительным начальным запасом денег в этой модели мы не сможем получить.

Сопоставляя балансовое условие (1.4) и бюджетные ограничения (1.2)-(1.3) получаем

(1.6)

. (1.7)

Так как слева в соотношении (1.7) стоит ни что иное, как масса денег в экономике в момент равная 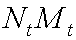, то соотношение (1.7) означает, что масса денег в экономике сохраняется. Следовательно, с каждым периодом количество денег на одного агента уменьшается в 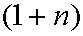раз.

Этот факт подчеркивает то, что в этой модели мы рассматриваем именно ту функцию денег, которая связана с передачей ценностей (потребления) во времени: будучи молодыми, мы продаем продукт людям из предшествующего поколения, чтобы потом купить продукт у людей из последующего.

Перепишем бюджетные ограничения в реальных терминах. Введем обозначения для реального денежного баланса 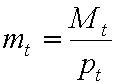, (1.8)

и инфляции : 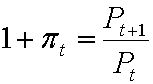. (1.9)

Тогда интегральное бюджетное ограничение потребителя приобретает вид:

, (1.10)

а соотношение (1.6) можно переписать как

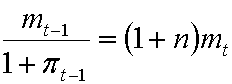(1.11)

На стационарной траектории выполнено

. (1.12)

Утверждение

На стационарной траектории цены падают с темпом 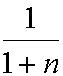, т. е. происходит дефляция:

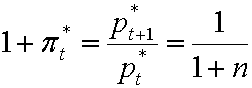
Доказательство

Запишем бюджетное ограничение второго периода жизни (1.3) для потребителей двух последовательных поколений, родившихся в и 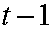, соответственно:

, (1.13)

. (1.14)

Поделив первое соотношение на второе, получим, что на стационарной траектории выполнено

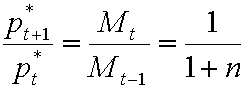(1.15)

Введем понятие оптимального стационарного распределения благ. В качестве такового примем распределение блага между агентами на стационарной траектории, максимизирующее полезность каждого при ресурсном ограничении всей экономики. То есть, это решение следующей задачи

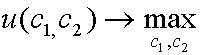(1.16)

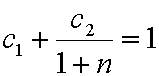(1.17)

Утверждение

На стационарной равновесной траектории реализуется оптимальное стационарное распределение благ.

Это утверждение вытекает из интегрального бюджетного ограничения (1.10) при условии (1.15) относительно уровня инфляции на стационарной траектории. То есть, на стационарной равновесной траектории агент решает задачу

,

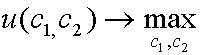s. t. ,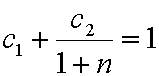

что в точности совпадает с задачей (1.1, определяющей оптимальное стационарное распределение благ.

Задача для размышления

Пусть . Найдите равновесные траектории для этой функции полезности.

Вы обнаружите, что имеется единственная равновесная траектория, а именно – стационарная, и она не зависит от уровня . При указанной выше функции полезности цена в первый момент времени будет выбираться так, что будет равно потреблению на стационарной траектории. При других функциях полезности может быть некоторый переходный процесс, сходящийся к стационарной траектории.

§ 2. Рост денежной массы в экономике и его последствия

Модифицируем задачу, введя в нее прирост денег в экономике. Теперь каждый период денежная масса будет увеличиваться. При этом необходимо определить, кто именно будет получать «новые» деньги. Как увидим в дальнейшем - это важный аспект, в определенной мере определяющий результат.

Паушальные трансферты пожилым

Рассмотрим случай, когда прирост денежной массы в момент в размере распределяется среди представителей старшего поколения, то есть задача агента, родившегося в момент , принимает вид

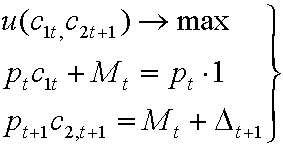(2.1)

Для простоты будем рассматривать ситуацию, когда агрегированная денежная масса в экономике растет с постоянным темпом , и из этого условия найдем необходимый размер трансферта .

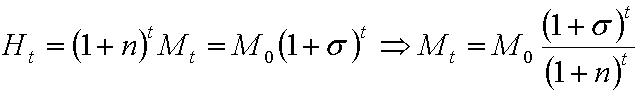- (2.2)

это следует из определения денежной массы. При этом разница между объемом денег в момент времени и в момент времени – это вливание в размере :

- (2.3)

закон сохранения денег с учетом их притока извне. Подставив (2.2) в (2.3), получим

(2.4)

Положим .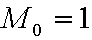

Рассмотрим стационарный режим (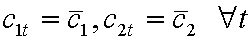) и вычислим темп инфляции в стационарном режиме.

Помножим бюджетное ограничение первого периода жизни поколения, родившегося в , на :

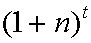(2.5)

Запишем это же соотношение для момента :

(2.6)

Поделив (2.6) на (2.5), и с учетом (2.2) получаем:

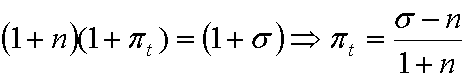(2.7)

Если мало, то 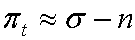: в стационарном режиме темп инфляции равен темпу роста денежной массы за вычетом темпа роста экономики.

Таким образом, задача, решаемая агентами на стационарной траектории, имеет вид:

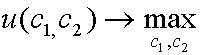, (2.8)

s. t. 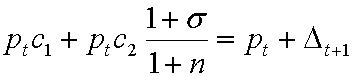, (2.9)

Поделим левую и правую часть бюджетного ограничения (2.9) на и, принимая во внимание то, что 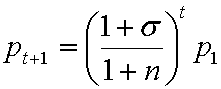, (2.10)

получаем:

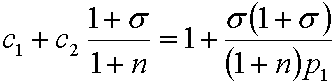. (2.11)

Максимизация 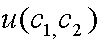на бюджетном ограничении (2.11) и дает стационарный режим экономики.

Нас интересует вопрос, как меняются реальные переменные и из-за вливания денег в экономику, то есть, как зависит реальное потребление от .

При 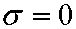бюджетное ограничение (2.11) совпадает с материальным балансом, которое по-прежнему имеет вид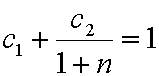

Если же , то интегральное бюджетное ограничение (2.11) отличается от материального баланса. Сопоставляя условия первого порядка оптимальной и равновесной задач на стационарной траектории (градиент пропорционален отношению коэффициентов при и в ограничении задачи), убедимся, что эти задачи дают разные решения, а, следовательно, потребление на стационарной траектории в экономике с вливанием денег отличается от стационарного решения в экономике с постоянной денежной массой. Очевидно, при такой постановке задачи деньги не являются супернейтральными.

Можно ли что-то сказать о том, кто, молодое или пожилое поколение, выиграет при таком способе вливания денег?

Ответ на этот вопрос в общем виде дать нельзя. Ответ на этот вопрос зависит от вида функции полезности.

Утверждение

Пусть функция полезности порождает нормальный спрос, обладающий свойством валовой заменимости. Тогда в стационарном режиме молодое поколение выигрывает, а старое поколение проигрывает от прироста денежной массы.

Доказательство

Если мы решаем задачу

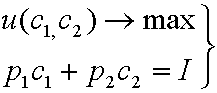, то (2.12)

нормальность спроса: решение задачи и увеличиваются с ростом ;

валовая заменимость: с ростом при фиксированном доходе увеличивается , и наоборот, с ростом растет потребление .

Рассмотрим нашу задачу: максимизируем на бюджетном ограничении (2.11), причем в соотношении (2.11) таково, что выполнено условие материального баланса

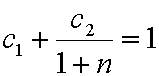(2.13)

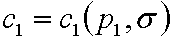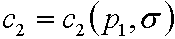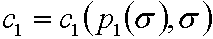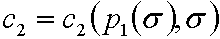То есть, решая задачу оптимизации на бюджетном ограничении (2.11), мы находим и , подставив которые в материальный баланс (2.13), мы найдем . Таким образом, мы определим и . Нас интересует, как и ведут себя при росте ?

Будем рассуждать от противного.

Пусть 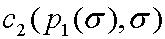возрастает по . Предположим, что при этом правая часть в (2.11) остается неизменной (фиксируем в доходной части). Тогда, исходя из условия валовой заменимости, должно увеличиться и, как следствие, должно уменьшиться. В силу нормальности спроса может вырасти при росте только, если правая часть в ограничении (2.11) выросла. Но тогда, в силу нормальности спроса, должно вырасти и . Однако, это невозможно в силу материального баланса (2.13). Следовательно, убывает по .

Графическая иллюстрация стационарного случая представлена на рисунке. Отрезок – это уравнение материального баланса и в случае экономики с постоянной денежной массой еще и бюджетное ограничение потребителя. Поэтому - точка равновесия. Она же является и точкой оптимального распределения, так как предельная норма замещения совпадает с наклоном общественного ресурсного ограничения.

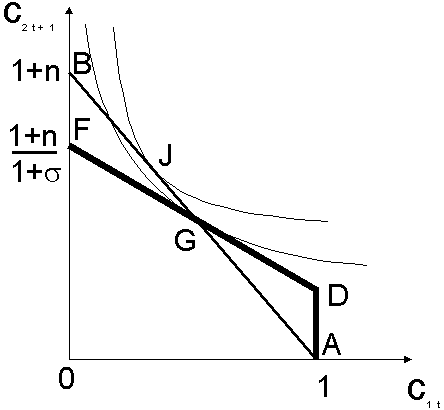В случае прироста денежной массы с темпом , бюджетное ограничение представляет собой отрезок 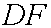, а балансовое условие по-прежнему соответствует . Очевидно, что в точке пересечения этих отрезков и будет реализовано равновесное распределение блага. При этом, в молодости потребление увеличивается, а в старости – уменьшается. Так же снижается общий уровень благосостояния: предельная норма замещения не совпадает с наклоном общественного ресурсного ограничения, следовательно, возможно Парето-улучшение.

Задача для размышления

Пусть .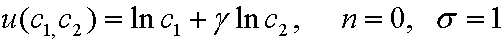

Убедитесь, что в стационарном состоянии в молодости агент выиграет, в пожилом возрасте проиграет, а в целом, полезность каждого агента уменьшится, т. к. распределение благ станет не оптимальным.

Если мы будем распространять прирост денежной массы среди представителей молодого поколения, то выигрыши и проигрыши в терминах потребления будут теми же. Как правило, при вливании денег в экономику, сопровождающимся ростом цен, проигрывают те, кто живут на сбережения, т. е. старики. Однако к этому выводу надо относиться осторожно: при однократном вливании, конечно, старики выиграют. Но если это будет повторяться многократно, каждый период, то в отдаленном будущем на стационарной траектории старики проиграют. Важно соотносить уровень прироста денег и темп роста цен.

Субсидии на денежные накопления

Рассмотрим иную схему увеличения денежной массы в экономике. Будем начислять каждому, кто сберег деньги в объеме , денежный процент, равный . Очевидно, при этом общая денежная масса в экономике будет расти с постоянным темпом . Определение равновесия остается тем же самым, т. к. не изменились параметры, которые входят в балансовое условие.

Задача агента при этом принимает вид

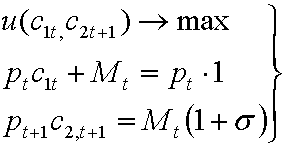(2.14)

Очевидно, что закон сохранения денежной массы при этом имеет вид:

. (2.15)

Сравнивая бюджетные ограничения молодых агентов двух последующих поколений, и учитывая (2.15) получаем выражение для инфляции на стационарной траектории:

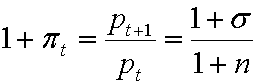(2.16)

Подставляя это соотношение в интегральное бюджетное ограничение задачи (2.14), получаем ограничение потребителя на стационарной траектории в виде:

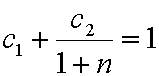, (2.17)

что в точности соответствует случаю без вливания денег в экономику.

Таким образом, мы видим, что в случае вливания новых денег в экономику посредством процентных платежей деньги оказываются супернейтральными – рост денежной массы не оказывает никакого влияния на реальные переменные в экономике.

Общий вывод: в рамках одной и той же модели, в зависимости от способа вливания денег в экономику деньги могут быть как супернейтральны, так и не супернейтральны