ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ"
г. МОСКВА
кафедра Теории и методики обучения математике в школе
СБОРНИК МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО ПОДГОТОВКЕ ДИПЛОМНЫХ РАБОТ ПО МЕТОДИКЕ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
МОСКВА, 2009
, , И. И. 3убарева, , .
Рекомендовано к печати Научно-методическим советом ГОУ ВПО МГПУ
Рецензенты: доктор пед. наук, профессор , кандидат пед. наук, доцент .
С23 . Сборник методических рекомендаций по подготовке дипломных работ по методике преподавания математики. / , , . – М.: ГОУ ВПО МГПУ, 20с.
OКоллектив авторов-составителей
O ГОУ ВПО МГПУ
Требования к содержанию и структуре дипломной работы по методике преподавания математики
Дипломная работа по методике преподавания математики представляет собой научно-методическое исследование, в котором выпускник применяет знание соответствующих теме разделов математики и дисциплин психолого-педагогического блока на практике.
Дипломная работа должна состоять из введения, теоретической и практической глав, заключения, списка использованной литературы и, если это необходимо, приложений.
Объём работы должен составлять 50-70 страниц вместе со списком использованной литературы, который не может включать меньше 15 источников по всему психолого-педагогическому блоку дисциплин (приложения при определении объема работы не учитываются).
Во введении студент должен обосновать актуальность выбранной темы, сформулировать цель работы, сформулировать задачи, решение которых, обеспечивает достижение цели, показать, какими методами исследования воспользовался.
Теоретическая часть работы должна содержать анализ психолого-педагогической литературы по теме исследования. В зависимости от темы в работе
• должны быть показаны знания общей психологии, либо знание психологических особенностей учащихся разных возрастных групп, либо психологии способностей, либо психологических требований к профессиональной деятельности педагога и пр.;
• должен быть проведен анализ имеющейся учебной и методической литературы по теме (желательно, если· это соответствует теме, анализ двух или более учебников федерального комплекта по выбору автора);
• должно быть продемонстрировано знание теоретических основ методики преподавания математики в приложении к выбранной теме и умение применять современные педагогические технологии в обучении математике (если это соответствует теме исследования).
В случае если это необходимо для раскрытия темы, работа должна содержать:
• исторический обзор развития либо математических идей, либо методической системы, либо форм организации образования;
• демонстрацию знания методики изучения соответствующих тем в зарубежной школе.
Практическая часть должна содержать вытекающие из теоретического исследования дипломника предложения по одному или нескольким видам работ из следующего списка:
• сценарии уроков, фрагментов уроков, группы уроков с использованием педагогических технологий, описываемых в дипломной работе;
• разработку планов или сценариев внеклассных мероприятий; планов, программ и содержания элективных, факультативных или кружковых занятий;
• создание системы или фрагмента системы упражнений для классной, домашней или внеклассной работы;
• разработку системы контроля текущих или итоговых знаний учащихся (это могут быть: тексты и решения самостоятельных и контрольных работ для проверки знаний учащихся с разным уровнем математической подготовки; вопросы для устного контроля; тестовые задания; задания для проведения зачетов); заданий для школьного этапа математических олимпиад и пр.
В практической части работы выпускник вправе показать, каким образом применялись его предложения в практике школы. В этом случае он должен дать описание проведенной опытной проверки: определить ее цели и задачи, показать формы проведения проверки, оценку полученных результатов.
Заключение должно содержать выводы по результатам проделанной работы.
В приложение может быть вынесен материал, иллюстрирующий основные положения, сформулированные в практической части работы. Например, полный список упражнений, часть которых с решением приведена в основной части; тексты контрольных работ, по которым проходила проверка результатов; диаграммы или графики, демонстрирующие результаты проведенной работы; иллюстративный материал к внеклассному мероприятию; образцы раздаточного материала и пр.
До рассмотрения предложенных в данном сборнике тем дипломных работ студенту желательно определить, какого типа работа ему наиболее интересна: теоретическая или практическая. В зависимости от склонностей рекомендуется выбрать тему:
• либо приближенную к вопросам общей методики с элементами психолого-педагогических исследований;
• либо связанную с анализом значительного количества психолого-педагогической и математической литературы и требующую серьезных самостоятельных обобщений и выводов;
• либо связанную с вопросами частных методик, в результате исследования которых нужно предложить методические рекомендации по изучению конкретной темы курса математики или разработать систему упражнений и пр.
Ниже приводятся варианты оглавлений дипломных работ различной ориентации. Даются выдержки из этих работ, содержащие формулировки целей, которые ставились в работах, и задачи, обеспечивающие реализацию поставленных целей.
Тема: «Формирование пространственных представлений учащихся в процессе изучения темы «Треугольники»
Содержание
Введение
Глава I. Возможные пути пропедевтики стереометрических знаний в процессе обучения геометрии в основной школе
§1. Понятие о пропедевтике как о методической проблеме
§2. Психолого-педагогическая характеристика учащихся 7-9 классов:
а) характеристика основных познавательных процессов в подростковом периоде;
б) условия формирования пространственных представлений подростка.
§3. Анализ существующих программ, учебников, стандартов с точки зрения реализации идеи пропедевтики
Глава II. Содержание пропедевтики стереометрических знаний в курсе геометрии 7 класса
§1. Включение стереометрического материала в систематический курс планиметрии
§2. Методические особенности реализации пропедевтики стереометрических знаний на примере изучения темы: «Признаки равенства треугольников» и «Медиана, биссектриса и высота треугольника» с учащимися 7 класса
§3. Примеры включения стереометрического материала в систематический курс основной школы.
Заключение
Литература
Целью дипломной работы является: изучение возможностей формирования у учащихся пространственных представлений в процессе обучения планиметрии и разработка соответствующей методики обучения на примере двух тем: «Признаки равенства треугольников» и «Медианы, биссектрисы и высоты треугольника».
Задачи дипломной работы:
• Проанализировать психолого-педагогическую, методическую и учебную литературу, связанную с проблемой формирования пространственных представлений учащихся.
• Сформулировать основные требования к пропедевтике стереометрических знаний при изучении планиметрии.
• Составить блоки задач по двум темам курса планиметрии на основании требований к пропедевтике стереометрических знаний.
• Разработать методику включения стереометрического материала в курс геометрии 7 класса на примере двух тем: «Признаки равенства треугольников» и «Медианы, биссектрисы и высоты треугольника».
Тема: «Золотое сечение на факультативных занятиях по математике в старших классах»
Содержание
Введение
Глава I. Общие вопросы организации и проведения факультативных курсов по математике для учащихся старших классов
§1. История возникновения и становления школьных факультативов по математике
§2. Виды внеклассной работы по математике и их цели
§3. Отбор содержания, форм и методов проведения факультативных занятий в старших классах
§ 4. Психолого-педагогическая характеристика старшеклассников
Глава II. Разработка факультативного курса «Золотое сечение» для учащихся старших классов
§1. Программа факультативного курса «Золотое сечение
§2. Структура факультативного курса «Золотое сечение»
§З. Содержание факультативного курса «Золотое сечение»
Занятие 1. Понятие и истоки золотого сечения
Занятие 2. Построение золотого сечения с помощью циркуля и линейки
Занятие 3. Свойства числа Ф
Занятие 4. Золотой треугольник
Занятие 5. Правильный пятиугольник и пентограмма
Занятие 6. Золотой треугольник
Занятие 7. Золотая спираль
Занятие 8. Золотое сечение и числа Фибоначчи
§4. Результаты педагогического эксперимента.
Заключение
Библиография
Приложения
Целью диплома является разработка факультативного курса «Золотое сечение» и методики его преподавания для учащихся старших классов.
Задачи исследования, необходимые решить для достижения поставленной цели:
• проанализировать методическую, педагогическую и психологическую литературу по теме дипломной работы;
• определить роль и место факультативных занятий в процессе обучения математике в школе;
• отобрать содержание факультативного курса «Золотое сечение»;
• составить психолого-педагогическую характеристику учащихся старших классов; разработать план факультатива «Золотое сечение» и конспекты конкретных занятий;
• представить диафильм «Божественная пропорция» на компьютере, созданный в интегрированной среде Power Point.
В ходе работы применялись различные методы исследования: изучение и анализ методической, педагогической и психологической литературы по теме работы; беседа; эксперимент; пробное преподавание.
Тема: «Решение текстовых задач в курсе алгебры 9 класса»
Содержание
Введение
Глава I. Научно - методические основы организации обучения решению текстовых задач в основной школе
§1. Текстовые задачи в истории математического образования
§2. Психолого-педагогические основы формирования умений решать текстовые задачи
§3. Функции задач в обучении математике
§4. Методические особенности обучения решению текстовых задач
§5. Анализ программ и учебников по математике
Глава II. Методические особенности обучения решению текстовых задач на уроках алгебры в девятом классе
§ 1. Анализ содержания курса алгебры в девятом классе
§2. Методические рекомендации по решению текстовых задач при изучении курса алгебры девятого класса
§3. Текстовые задачи в обобщении курса алгебры основной школы
Заключение
Приложения
Список литературы
Целью данной работы является разработка системы обобщения и систематизации способов решения текстовых задач в курсе алгебры девятого класса.
Для достижения поставленной цели решались следующие задачи:
• Изучить психолого-педагогическую литературу по данной теме.
• Проанализировать действующие учебники по алгебре для девятого класса и программу по математике для общеобразовательных школ.
• Разработать вариант планирования введения текстовых задач в курс алгебры девятого класса.
• Разработать систему задач для решения в курсе алгебры девятого класса в течение учебного года и на уроках обобщающего повторения.
Тема: «Формирование понятия производной в курсе алгебры и начал анализа в десятых классах гуманитарного направления»
Содержание
Глава I. Научно-методические основы преподавания математики в классах гуманитарного направления
§ 1. Профильная дифференциация в России и за рубежом
§ 2. Профильная дифференциация в обучении математике в современной отечественной школе
§ 3. Особенности психофизиологического облика школьников. Склонности и способности учащихся
§ 4. Значение индивидуальной памяти в обучении
§ 5. Особенности познавательной деятельности учащихся
§ 6. Цели и задачи обучения математике в гуманитарных классах
§ 7. Особенности учебников по математике для гуманитариев
Глава II. Методические особенности изучения производной в классах гуманитарной направленности
§ 1. Понятие и методические требования к системе упражнений в методике преподавания математике
§ 2. Отбор и конструирование упражнений
§ 3. Особенности системы упражнений при формировании понятия производной в классах гуманитарного профиля
§ 4. Организация изучения темы «Производная» в классах гуманитарного направления
§ 5. Пропедевтика введения понятия производной
§ 6. Введение понятия производной
§ 7. Развитие учащихся при формировании понятия дифференциала и нахождения производных
§ 8. Особенности изучения приложений производной в гуманитарных классах
§ 9. Опытная проверка введения темы «Производная»
Заключение
Приложение 1. Упражнения, расширяющие систему упражнений учебника «Математика 11» авторов и др. для гуманитарных классов
Приложение 2. Организация контроля усвоения темы
Литература
Цель работы:
– изучить особенности обучения математике учащихся классов гуманитарного профиля и разработать методику формирования понятия производной у учащихся гуманитарных классов.
Для достижения поставленной цели необходимо было решить следующие задачи:
• изучить психолого-педагогическую литературу по поставленной проблеме;
• изучить существующие программы для общеобразовательной и профильной школ, в которых особое внимание уделить курсу А;
• провести анализ существующих учебников по алгебре и началам анализа;
• разработать систему уроков и упражнений для реализации поставленной цели.
Тема: «Изучение правильных многогранников в условиях профильного обучения»
Содержание
Введение
Глава I. Психолого-педагогические основы дифференцированного обучения в школе
§1. Исторические аспекты дифференцированного обучения в школе
§2. Различные подходы к понятию дифференцированного обучения
§3. Уровневая и профильная формы дифференциации
§4. Психолого-педагогические особенности учащихся гуманитарных и математических классов
Глава II. Методические особенности изучения правильных многогранников в условиях профильного обучения
§ 1. Анализ современных учебников по геометрии
§2. Сравнительный анализ темы «Правильные многогранники» в курсе геометрии старшей профильной школы
§3. Разработка уроков для классов гуманитарного направления
3.1. Пояснительная записка
3.2. Конспект 1
3.3. Конспект 2
§4. Разработка уроков для классов естественнонаучного направления
4.1. Пояснительная записка
4.2. Конспект 1
4.3. Конспект 2
§5. Результаты педагогического эксперимента
Заключение
Библиография
Приложения
Целью дипломной работы является выявление методических особенностей изучения правильных многогранников с учащимися старших классов в условиях профильного обучения и разработка соответствующих конспектов занятий и методических рекомендаций.
Поставленная цель определила следующие задачи:
• Проанализировать психолого-педагогическую, учебную, методическую литературу, связанную с проблемой изучения раздела геометрии «Правильные многогранники» в условиях профильного обучения.
• Изучить состояние и перспективы системы профильного обучения учащихся 10 - 11 классов.
• Составить психолого-педагогическую характеристику учащихся гуманитарных и математических классов.
• Рассмотрев методические особенности изучения многогранников в старшей школе, представить конспекты уроков геометрии по теме «Правильные многогранники» для классов двух профилей.
Тема: «Методические особенности изучения математики в 6 классе коррекционно-развивающего обучения»
Содержание.
Введение
Глава I. Научно-методические основы обучения математике в классах коррекционно-развивающего обучения
§1. История развития классов коррекционно-развивающего обучения
§2. Психолого-педагогическая характеристика учащихся в классах коррекционно-развивающего обучения
§ 3. Принципы и методы выявления нарушений умственного развития детей
§4. Анализ методического обеспечения обучения математике в классах коррекционно-развивающего обучения
§5. Особенности организации учебного процесса в классах коррекционно-развивающего обучения
Глава II. Методические особенности обучения теме «Положительные и отрицательные числа» в классе коррекционно-развивающего обучения
§1. Анализ содержания учебного материала по теме
§2. Организация изучения темы в 6-х классах коррекционно-развивающего обучения
§3. Методические особенности формирования понятия целого числа в классах коррекционно-развивающего обучения
§4. Результаты опытной проверки обучения учащихся 6 класса по предложенной методике
Заключение
Приложение I
Приложение II
Литература
Целью данной работы является изучение методических особенностей обучения математике в классах коррекционно-развивающего обучения и разработка рекомендаций по изучению одной из тем курса.
Для достижения поставленной цели потребовал ось решение следующих задач:
• изучить психофизиологические особенности развития детей, обучающихся в классах коррекционно-развивающего обучения;
• сформулировать требования к изложению учебного материала в 6 классе коррекционно-развивающего обучения;
• проанализировать имеющееся математическое и методическое обеспечение процесса обучения в классах коррекционно-развивающего обучения;
• разработать авторский вариант методических рекомендаций по изучению темы "Положительные и отрицательные числа" в 6 классе коррекционно-развивающего обучения.
При решении данных задач использовались следующие методы:
• анализ психолого-педагогической литературы;
• анализ программ и учебников;
• анкетирование учащихся;
• беседы с опытными учителями;
• опытная проверка разработанных рекомендаций.
Примерная последовательность действий при выполнении дипломной работы
1. Изучение и конспектирование рекомендованной литературы (за основу выбирается литература, предложенная руководителем или в данном сборнике, затем список расширяется за счет работ, которые дипломник находит самостоятельно).
2. Составление подробного плана раскрытия темы работы (как результат анализа использованной литературы и обсуждения с руководителем оглавления работы).
З. Определение совместно с руководителем сроков завершения каждого этапа работы над темой.
4. Написание теоретической части работы на основе изученной литературы.
5. Разработка собственных предложений по практической части работы, если возможно, проведение проверки ее применения.
6. Описание практической части работы.
7. Консультация с руководителем о написании окончательного варианта работы и формулировании выводов (заключения).
8. Оформление дипломной работы (в печатном виде, но без переплета).
9. Подготовка работы к рассмотрению на заседании кафедры.
10. Доработка по замечаниям, данным на заседании кафедры.
11. Переплет и передача работы для рецензирования.
Общие требования к оформлению дипломной работы
Текст дипломной работы должен быть набран на компьютере. Текст пишется через 1,5 интервала на одной стороне листа, рекомендованная гарнитура (стиль) шрифта “Times New Roman Cyr”, кегль (размер) – 12. Поля страницы должны быть следующими: сверху – 1,5 см, снизу – 1,5 см, слева – 2,5 см, справа – 1 см. Нумерация страниц располагается в правом верхнем углу.
К каждому экземпляру дипломной работы прилагается рецензия преподавателя (куратора, оппонента) и отзыв научного руководителя. Рецензия и отзыв вкладываются в переплетенную дипломную работу, но не прошиваются.
Дипломная работа сдается в 2-х экземплярах. Дискета (диск) с дипломной работой в обязательном порядке прилагается к каждому экземпляру диплома.
Во всей дипломной работе соблюдается научный стиль изложения и единый стиль оформления. Между параграфами, главами и частями дипломной работы должны быть предложения – связки, чтобы не было ощущения "разорванного текста".
В тексте работы, доказывая свою точку зрения, следует в обязательном порядке употреблять вместо местоимения "я" – "мы".
Например: "Мы считаем, что, …", "Мы думаем, что, ...", "Мы делаем вывод…" и т. п.
Образец оформления титульного листа приведен на следующей странице. Титульный лист не нумеруется!
Оглавление идет отдельным листом после титульного листа дипломной работы. Оно фактически представляет собой содержание дипломной работы с указанием глав, параграфов работы и страниц, на которых они расположены. Лист с оглавлением также не нумеруется!
Собственно текст работы начинается на третьей странице с введения.
Каждая глава, заключение, приложения (если таковые имеются), список литературы начинаются с новой страницы. Названия глав, параграфов, приложений, список литературы выделяются жирным шрифтом.
Список использованной литературы формируется по алфавиту. Здесь приводится алфавитный список литературы или других источников информации, использованных при написании дипломной работы. (См. ниже "Библиографическое описание документов").
Требования к оформлению библиографии, ссылок и сносок
При ссылке в тексте дипломной работы на какую-либо книгу или статью, следует указать в квадратных скобках номер, под которым этот первоисточник числится в списке литературы. Если в работе приводится цитата из источника, то рядом в квадратных скобках после условного номера источника через запятую указывается номер страницы в книге или статье, откуда взята цитата (например, запись [7, 20] означает, что цитата взята из статьи или книги, которая в списке значится под номером 7, а текст цитаты находится на 20 странице).
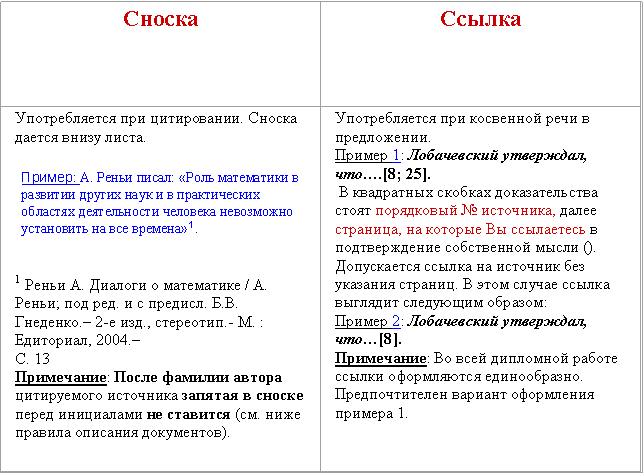

Библиографическое описание любого документа – объекта сноски – включают в библиографический список только один раз. При повторных сносках на этот документ цитируемые или упоминаемые страницы указывают в отсылке в тексте. (В данном случае см. Ссылка. Пример 1).
В повторных сносках только на одну работу данного автора (авторов) основное заглавие и следующие за ним повторяющиеся элементы опускают, указывают № тома или выпуск и страницы, на которые ссылаются.
Первичная сноска:
Пример:
Размышления натуралиста.– М., 1977.– Кн. 2: Научная мысль как планетное явление.– С. 39.
Вторичная сноска на тот же документ:
Пример:
И.– Кн. 2.– С. 10.
В расположенных подряд библиографических описаниях (сносках) совпадающие сведения во втором и последующем библиографических описаниях заменяют словами: "То же", "Его же" и т. п.
![]() Образец оформления титульного листа дипломной работы 1,5 см.
Образец оформления титульного листа дипломной работы 1,5 см.
Департамент образования г. Москвы
ГОУ ВПО города Москвы
"МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра (полное название кафедры)
2,5 см. 1 см.
Дипломная работа
По теме: "……….."
По специальности № "Название специальности"
Студентки (та)
5 курса д (в)/о
Научный руководитель:
Должность, звание
Допущена к защите
"___" _______ 200_ г.
подпись науч. рук.
/Расшифровка подписи/
![]() Москва, 2009
Москва, 2009
1,5 см.
Библиографическое описание документов
Для библиографического описания документов используется информация с титульного листа книги и его оборота или сведения о статье (для печатных изданий), адресная строка сайта (для интернет-публикаций), обложка СD-диска. Согласно ГОСТам библиографического описания документов за 2003 год, в описании документов в квадратных скобках указывается тип носителя документа: [Текст], [Электронный ресурс], [Электронный документ]. Тип носителя документа в сносках НЕ УКАЗЫВАЕТСЯ.
Индивидуальный автор.
Описания, выполненные под заголовком.
КНИГИ
Общие замечания:
В области выходных данных, если встречаются два - три города или два - три издательства, то города пишутся через";" а издательства через ":" после перечисления городов. В сведениях об ответственности автора за знаком "/" указываются инициалы и фамилии автора (ов) без "," между инициалами и фамилией. Знак ".–" является неразрывным символом и не может находиться на разных строчках или в начале строки. Знак "/" не может оставаться в конце строки. Лучше перенести его в начало следующей, и продолжить описание документа.
1, 2, 3 автора
1 автор:
Схема описания: Фамилия, И. О. автора (Заголовок описания). Заглавие (название) книги : Сведения, относящиеся к заглавию [Тип носителя документа] / Сведения об ответственности автора; Сведения об ответственности иных лиц, участвующих в оформлении книги (если они есть).– Сведения об издании (2-е изд., испр. и доп., перераб. и т. д.– если они есть).– Выходные данные книги (город : издательство, год издания).– Количественная характеристика (объем) издания : сведения об иллюстративном материале (илл., табл., схемы).– (Область серии).– Область примечаний.
Пример: Зайкин, М. И. Развивай геометрическую интуицию: 5-9 кл. : Кн. для учащихся [Текст] / .– М.: Просвещение : Владос, 1995.– 112 с. : ил.
2 автора:
Схема описания: Фамилия, И. О. первого автора (Заголовок описания). Заглавие (название) книги: Сведения, относящиеся к заглавию [Тип носителя документа] / Сведения об ответственности авторов (указываются все 2 автора); Сведения об ответственности иных лиц, участвующих в оформлении книги (если они есть).– Сведения об издании (2-е изд., испр. и доп., перераб. и т. д.– если они есть).– Выходные данные книги (город : издательство, год издания).– Количественная характеристика (объем) издания : сведения об иллюстративном материале (илл., табл., схемы).– (Область серии).– Область примечаний.
Пример: Шарыгин, И. Ф. Наглядная геометрия: 5-6 кл. : Пособие для общеобразоват. учеб. заведений [Текст] / , .– 3-е изд., стереотип.– М.: Дрофа, 2000.–
192 с.: ил.
3 автора:
Схема описания: Фамилия, И. О. первого автора (Заголовок описания). Заглавие (название) книги : Сведения, относящиеся к заглавию [Тип носителя документа] / Сведения об ответственности авторов (указываются все 3 автора); Сведения об ответственности иных лиц, участвующих в оформлении книги (если они есть).– Сведения об издании (2-е изд., испр. и доп., перераб. и т. д.– если они есть).– Выходные данные книги (город : издательство, год издания).– Количественная характеристика (объем) издания : сведения об иллюстративном материале (илл., табл., схемы).– (Область серии).– Область примечаний.
Пример: Виленкин, Н. Я. Дифференциальные уравнения: Учеб. пособие для студентов-заочников IV курса физ.– мат. фак. [Текст] / , , .– М.: Просвещение, 1984.– 176 с.
Описания, выполненные под заглавием.
(4 и более авторов, сборники).
4 и более авторов:
Математический анализ в вопросах и задачах: Учеб. пособие [Текст] / , , и др.; Под ред. .– 3-е изд., испр.– М.: Физ.– мат. лит., 2000.– 480 с.
коллективный автор.
Описания, выполненные под заголовком.
(труды институтов, университетов, организаций, конференции, семинары)
Схема описания: Заголовок описания (Название семинара, конференции) (Год проведения; место проведения семинара). Труды семинара, (дата и год проведения) [Тип носителя] / Сведения об ответственности издающей организации; Сведения об ответственности авторского коллектива.– Выходные данные.– Количественная характеристика (объем) издания.– (Область серии – если есть).– Область примечания.
Пример: Всесоюз. семинар зав. каф. и преподавателей геометрии пед. ин-тов СССР (1972; Тбилиси). Труды Всесоюзного семинара заведующих кафедрами и преподавателей геометрии педагогических институтов СССР, (19-22 декабря 1972 года) [Текст] / М-во просвещения СССР. М-во высш. и сред. спец. образования Грузин. ССР; Ред. .– Тбилиси: Изд-во Тбилис. ун-та, 1974.– 269 с. : ил.– Библиогр. в конце ст.
Описания, выполненные под заглавием.
Схема описания: Заглавие описания (Название книги, сборника) [Тип носителя] / Сведения об ответственности издающей организации; Сведения об ответственности авторского коллектива.– Выходные данные.– Количественная характеристика (объем) издания.– (Область серии – если есть).– Область примечания.
Пример: Вопросы дифференциальной и неевклидовой геометрии / Моск. гос. пед. ин-т им. . Каф. геометрии; Отв. ред. .– М.: Изд-во МГПИ, 1967.– 435 с.: ил.– (Ученые записки МГПИ им. В.И. Ленина; N 271).– Библиогр. в конце ст.– На обл. указана только сер.
Заголовок, содержащий обозначение документа
(ГОСТ, программы и т. п.)
Законодательные документы
Описание под заголовком
Российская Федерация. Законы. Закон об образовании : ( в ред. Федерал. законов от 01.01.2001 , от 01.01.2001 , от 01.01.2001 ; 102-ФЗ, от 01.01.2001 , от 01.01.2001 , от 01.01.2001 , от 25.№ 71- ФЗ, от 01.01.2001 , с изм., внесенными Постановлением Конституц. Суда РФ от , ФЗ от 01.01.2001 , от 01.01.2001 ) [Текст] / РФ.– СПб. : Изд-во , 2002.– 61с.– (Федеральный закон ).– ISBN -9.
Описание под заглавием
Об образовании : закон РФ: (Ведомости Съезда НД РФ и ВС РФ, 1992, № 30, ст. 1797): в ред. ФЗ.– 13-е изд.– М. : Ось-89, 2007.– 95с.– (Федеральный закон)
ГОСТ
ГОСТ 7.9-95 (ИСО 214-76). Реферат и аннотация. Общие требования : Межгос. стандарт.– Введ. [Текст] // Стандарты по издательскому делу / Сост.: , .– М., 1998.– С. 132-137.
Программы
Математика: 5-11 кл. : Программы. Тематическое планирование : Для общеобразоват. шк., гимназий, лицеев. [Текст] / М-во образования РФ; Сост.: , .– М.: Дрофа, 2000.– 320 с.
НЕОПУБЛИКОВАННЫЕ ДОКУМЕНТЫ
Автореферат
Общие замечания: Диссертации и авторефераты диссертаций описываются по правилам описания книг одного автора.
Белобородова, С. В. Профессионально-педагогическая направленность историко-математической подготовки учителей математики в педвузах: автореф. дис. … канд. пед. наук : 13.00.02 [Текст]
/ .– Защищена 13.01.01; Утв. 08.12.99.– М., 1999.– 23 с.– На правах рукописи.– Библиогр.: С. 22-23.
Диссертация
Сусык, С. Ю. Реализация концепта "терроризм" в дискурсе печатных средств массовой информации : дис. ... канд. филол. наук 10.02.19; защита 10.11.08 / ; науч. рук. ; Федер. агентство по образованию РФ, ГОУ ВПО "Челяб. гос. ун-т".– Челябинск, 2008.– 206л.– На правах рукописи.– Библиогр.: л. 182-203.
Электронные ресурсы удаленного доступа
Документы из сети Интернет
Описание необходимой информации, взятой с сайтов, дается по общим правилам описания журнальных статей, приведенных ниже, но вместо выходных данных журнала (Заглавие, год, номер, количество стр.) пишется адресная строка сайта. В электронной версии дипломной работы (на диске, на дискете) в библиографии ссылки должны быть активными.
Схема описания: Фамилия, И. О. автора публикации. Заглавие публикации [Электронный документ] / автора (ов).– (http: //www.адрес сайта). Дата обращения к документу (когда просмотрен документ) в формате "число. месяц. год."
Пример: Пестерева, В. Л. О работе в классах КРО [Электронный документ] / .– (http://www. pspu. *****). 12.04.2000
Документ, извлеченный из цифровой базы данных
Схема описания: Автор. Заглавие. // Заглавие источника [Вид документа] / Сведения об источнике. Заглавие базы данных (http://www.адрес базы данных). Регистрационный № в базе данных. Дата обращения.
Пример: Alzami, Mansour А. Perseptions of Internet use as academic library services' delivery medium for Web-based sourses [Электронный документ] / The Florida State University.– 2002, 153 Quest (http://www. /). AAT 30340
Адреса сайтов в библиографии располагаются общем алфавитном порядке с описаниями из других источников информации.
Электронные ресурсы локального доступа (CD-ROM, DVD)
Данные для описания электронных ресурсов, берутся с обложек описываемого ресурса.
Схема описания: Фамилия, И. О. автора (ов) если есть. Заглавие ресурса [Тип носителя]
/ Сведения об ответственности.– версия; емкость ресурса.– Выходные данные.– количество дисков : информация о приложениях.– (серия, в которой выпущен ресурс).– Минимальные системные требования.– Примечания.
Пример: Практический курс Windows XP [Электронный ресурс] / М-во образования РФ; Федеральная программа развития образования.– версия 2.0; 500 Мб.– М. : Кирилл и Мефодий: Uniar : СГУ, Б. г.– 1 электронный опт. диск (CD-ROM) : зв., цв.; 12 см. + Инструкция для пользовал.).– (Практические курсы по информационным технологиям).– Миним. систем. требования: IBM PS: MS Windows 98 и выше; процессор Pentium; 32 Мбайт ОЗУ; SVGA-видеокарта (1024х768, High Color 16 бит); зв. карта; MS Windows совместимая мышь; CD-ROM.– Диск и сопроводит. материал помещены в контейнер 12х14 см.
Описания составных частей документов
(статьи из газет, журналов, сборников).
Общие замечания: Отдельные статьи из периодических изданий описываются по общим правилам описания книг 1 – 3 авторов. Разница в том, что после заглавия (названия) статьи и сведений об ответственности автора(ов) "/" ставятся две косые черты "//", далее описание проводится, согласно схеме описания. Знак "//", также как и знак "/" не может быть оставлен в конце строки. Лучше перенести его в начало следующей, и продолжить описание документа.
Статья из журнала:
Садовничий, В. О новой волне "утечки умов" и не только [Текст] / В. Садовничий // Alma mater.– 2002.– № 1.– С. 3-4
Если научный журнал выходит в томах или номерах, от описание выглядит следующим образом:
Андрианов, -функция ортогональных групп целочисленных положительно-определенных квадратичных форм [Текст] / // Успехи мат. наук.– 2006.– Т. 61, вып. 6.– С. 3-44.
или:
Андрианов, -функция ортогональных групп целочисленных положительно-определенных квадратичных форм [Текст] / // Успехи мат. наук.– 2006.– Т. 61, № 6.– С. 3-44.
Статья из газеты:
Общие замечания: В случае газетной публикации схема описания выглядит следующим образом: после № выпуска в скобках ставится число и месяц выхода газеты.
Минаева, С. Алгебраические дроби : 8 кл. [Текст] / С. Минаева, С. Суворова, Г. Ковалева и др.
// Математика : прил. к газ. "Первое сентября".– 2002.– 1-7 окт. (№ 37).– С. 15-17.
Статья из сборника:
Схема описания: Заглавие статьи [Тип носителя] // Заглавие сборника : Сведения, относящиеся к заглавию / Сведения об ответственности авторского коллектива (первые 3 автора и др.); Сведения об ответственности иных лиц (редактора, составителя).– Сведения об издании.– Выходные данные.– Количественная характеристика (объем) издания.– Страницы, на которых расположена статья.
Пример: Теоремы об ограниченности непрерывных функций [Текст] // Математический анализ в вопросах и задачах : Учеб. пособие / , , и др.; Под ред. .– 3-е изд., испр.– М., 2000.– С. 108-112.
Книги и периодические издания на иностранном языке
Описание книг и периодических изданий дается на языке оригинала (нем., англ., франц. и т. д.) по правилам библиографического описания соответствующих документов, приведенным выше. Библиографические описания источников, выполненные на иностранном языке, располагаются отдельным алфавитным рядом после всего списка русскоязычной литературы.
Книги:
Fletcher, T. J. Microcomputers and Mathematics in Schools: A discussion paper by T. J. Fletcher, HMI [Текст] / T. J. Fletcher.– Б. м.: Departament of Education and Science, 1983.– 39 р.
Периодика:
Bungartz, P. The Role of Mathematics in Educational Policies [Текст] / P. Bungartz, R. Strasser // Germany.– 1992.– juli. (№ 000).– 15 рp.
Необходимые сокращения в элементах библиографического описания
Город (Место издания документа):
• Москва – М.,
• Ленинград – Л., Петербург/Петроград – Пб./Пг., Санкт-Петербург – СПб.,
• Нижний Новгород – Н. Новгород
• Ростов–на-Дону – Ростов н/Д.
Некоторые слова и словосочетания, не являющиеся первыми словами в описании:
- школа – шк.,
• язык – яз.,
• упражнение – упр. (при цифрах),
• урок – ур. (при цифрах),
• учебник, учебный – учеб.,
• планирование – планир.,
• план – пл.,
• педагогический – пед.,
• класс – кл. (при цифрах),
• издание – изд.,
• издательство – изд-во (Издательство области, института и т. п.) В остальных случаях слово "изд-во" не пишется.
Варианты сокращений названий некоторых издательств
В библиографическом описании документа издательство пишется без кавычек, сокращений (ООО, АО и т. п.), и без слова издательство, кроме особо оговоренного случая.
Ассоциация XXI век – Ассоц. XXI век
Высшая школа – Высш. шк.
Издательство Белорусского университета – изд-во Белорус. Ун-та
Московская академия развития образования – Моск. акад. развития образования
Московские учебники – Моск. учеб.
Московский психолого–социальный институт – Моск. псих-соц. ин-т
Московский центр непрерывного математического образования – МЦНМО
Наука. Главная редакция физико-математической литературы – Наука. Гл. ред. физ.– мат. лит.
Российская энциклопедия – Рос. энциклопедия
Советская энциклопедия – Сов. энциклопедия
Школьная книга - Школьная кн.
Сокращения месяцев года
Действительны ТОЛЬКО для описаний статей из периодических изданий. Все остальные месяцы пишутся полностью.
Январь – янв., февраль – февр., апрель – апр., август – авг., сентябрь – сент., октябрь – окт., ноябрь – нояб., декабрь – дек.
ОБРАЗЕЦ оформления БИБЛИОГРАФИИ В ДИПЛОМНОЙ РАБОТЕ
Библиография
1.Андрианов, А. Н. Дзета-функция ортогональных групп целочисленных положительно-определенных квадратичных форм [Текст] / // Успехи мат. наук.– 2006.–
Т. 61, вып. 6.– С. 3-44.
2. Белобородова, С. В. Профессионально-педагогическая направленность историко-математической подготовки учителей математики в педвузах : Автореферат дис. на соискание ученой степени канд. пед. наук : 13.00.02 [Текст] / .– Защищена 13.01.01; Утв. 08.12.99.– М., 1999.– 23 с.– Библиогр.: С. 22-23.
3. Виленкин, Н. Я. Дифференциальные уравнения : Учеб. пособие для студентов-заочников IV курса физ.– мат. фак. [Текст] / , , .– М. : Просвещение, 1984.– 176 с.
4. ГОСТ 7.9-95 (ИСО 214-76). Реферат и аннотация. Общие требования : Межгос. стандарт.– Введ. [Текст] // Стандарты по издательскому делу / Сост.: , .– М., 1998
5. Зайкин, М. И. Развивай геометрическую интуицию : 5-9 кл. : Кн. для учащихся [Текст]
/ .– М. : Просвещение : Владос, 1995.– 112 с.: ил.
6. Математика: 5-11 кл. : Программы. Тематическое планирование : Для общеобразоват. шк., гимназий, лицеев. [Текст] / М-во образования РФ; Сост.: , .–
М. : Дрофа, 2000.– 320 с.
7. Математический анализ в вопросах и задачах: Учеб. пособие [Текст] / , , и др.; Под ред. .– 3-е изд., испр.– М. : Физ.– мат. лит., 2000.– 480 с.
8. Минаева, С. Алгебраические дроби: 8 кл. [Текст] / С. Минаева, С. Суворова, Г. Ковалева и др. // Математика: прил. к газ. "Первое сентября".– 2002.– 1-7 окт. (№ 37).– С. 15-17.
9. Пестерева, В. Л. О работе в классах КРО [Электронный документ] / .– (http://www. pspu. *****). 12.04.2000
10. Практический курс Windows XP [Электронный ресурс] / М-во образования РФ; Федеральная программа развития образования.– версия 2.0; 500 Мб.– М. : Кирилл и Мефодий : Uniar : СГУ, Б. г.– 1 электронный опт. диск (CD-ROM) : зв., цв.; 12 см. + Инструкция для пользователя (2л.).– (Практические курсы по информационным технологиям).– Миним. систем. требования: IBM PS: MS Windows 98 и выше; процессор Pentium; 32 Мбайт ОЗУ; SVGA-видеокарта (1024х768, High Color 16 бит); зв. карта; MS Windows совместимая мышь; CD-ROM.– Диск и сопроводит. материал помещены в контейнер 12х14 см.
11. Садовничий, В. О новой волне "утечки умов" и не только [Текст] / В. Садовничий // Alma mater.– 2002.– № 1.– С. 3-4
12. Теоремы об ограниченности непрерывных функций [Текст] // Математический анализ в вопросах и задачах : Учеб. пособие / , , и др.; под ред. .– 3-е изд., испр.– М., 2000
13. Шарыгин, И. Ф. Наглядная геометрия: 5-6 кл. : Пособие для общеобразоват. учеб. заведений [Текст] / , .– 3-е изд., стереотип.– М. : Дрофа, 2000.– 192 с.: ил.
14. Alzami, Mansour А. Perseptions of Internet use as academic library services' delivery medium for Web-based sourses [Электронный документ] / The Florida State University.– 2002, 153 Quest (http://www. /). AAT 3034039.
15. Bungartz, P. The Role of Mathematics in Educational Policies [Текст] / P. Bungartz, R. Strasser
// Germany.– 1992.– juli. (№ 000).– 15 рp.
16. Fletcher, T. J. Microcomputers and Mathematics in Schools : A discussion paper by T. J. Fletcher, HMI [Текст] / T. J. Fletcher.– Б. м. : Departament of Education and Science, 1983.– 39 c.
Темы дипломных работ
1. Общая методика
Методика формирования специальных (предметных) умений на уроках математики
Различные трактовки понятия умения (в педагогике, в психологии, в методике преподавания математики). Примеры специальных (предметных) умений, формируемые при обучении математике.
Методика формирования умений в курсе алгебры (геометрии, алгебры и начал анализа), реализующая один из выбранных подходов.
Литература: [66], [106], [165], [264], [308].
Методика обучения математическим доказательствам
Понятие о математическом доказательстве, примеры доказательств. Обучение готовым доказательствам.
Доказательство теорем: открытие теоремы: доказательство, закрепление,
Различные общие методы доказательств (аналитический, синтетический с анализом Евклида, от противоположного и др.), специальные методы доказательств в геометрии, в алгебре. Примеры.
Литература: [55], [66], [93], [264], [308].
Дополнительная литература
Методика организации самостоятельной деятельности учащихся на уроках математики
Понятие о самостоятельной деятельности учащихся на уроках математики и ее структуре.
Виды самостоятельной деятельности на уроках математики, характеристика каждого вида.
Организация самостоятельной деятельности учащихся на различных этапах урока математики.
Сравнительный анализ доли самостоятельной работы школьников в основной и старшей школе.
Литература: [85], [184], [187], [193], [194], [250], [254], [283], [308].
Дополнительная литература
Методика работы с учебником в процессе обучения математике
Средства обучения математике. Учебник математики: функции, виды, структура и содержание. Учебник – книга для учителя или для ученика?
Методические приемы работы с учебными пособиями по математике. Методика работы с учебником на разных этапах урока и во внеурочное время.
Система работы с учебником (в определенном классе или при изучении определенной содержательной линии школьного курса).
Литература: 232, 150, 191-197.
Дополнительная литература
Дидактическая игра в обучении математике
Понятие о дидактической игре и ее структуре. Функции дидактических игр.
Дидактические игры в активизации познавательной деятельности учащихся. Виды дидактических игр в зависимости от назначения и методики проведения, различающиеся по цели, темпу, кратности применения, методике проведения. Наглядные средства при использовании дидактических игр.
Особенности дидактических игр для основной и старшей школы. Методика подготовки и поведения различных дидактических игр. Примеры дидактических игр на уроках алгебры (геометрии, алгебры и начал анализа).
Анализ возможностей действующих учебников математики для использования дидактических игр.
Методика использования дидактических игр при изучении различных тем.
Литература: [67], [70], [85], [146], [183], [194], [214], [251], [252], [295], [186], [193].
Дополнительная литература
Методика проведения уроков заключительного повторения
Повторение. Характеристика различных видов повторения. Заключительное повторение: цели, принципы отбора содержания и выбора методов обучения.
Различные виды учебной работы учащихся на уроках заключительного повторения.
Активизация познавательной деятельности учащихся на уроках заключительного повторения.
Разработка методических рекомендаций по подготовке уроков заключительного повторения по курсу алгебры (алгебры и начал анализа, геометрии).
Литература: [85], [93], [94], [106], [138], [146], [164].
Дополнительная литература
Методика поведения уроков дифференцированной работы
Урок математики, типизация уроков. Понятие об уроке дифференцированной работы, примеры.
Основные принципы проведения уроков дифференцированной работы на различных этапах обучения (этапы объяснения нового материала, закрепления, систематизации знаний, повторения, проверки знаний).
Формы проведения уроков дифференцированной работы, примеры уроков.
Литература:
1. Проблемы совершенствования преподавания математики в средней школе. М.: ротапринт СССР. 1986.
2. [187], [211], [215].
Дополнительная литература
Применение новых педагогических технологий в обучении математике
Понятие педагогической технологии, ее компоненты. Классификация педагогических технологий по уровню применения.
Примеры педагогических технологий общетеоретического уровня.
Использование педагогических технологий обучения математике: построение алгоритма функционирования и алгоритма управления.
Практическая часть состоит в построении алгоритма функционирования и алгоритма управления технологии (по выбору студента), например, технологии модульного обучения, моделирующего обучения и др.
Литература:
1. Новые педагогические и информационные технологии в системе образования / , , ; Под ред. ? М.: Академия, 2005.
2. Селевко образовательные технологии. / .?М.: Народное образование, 1998.
3. Гузеев результатов образования и образовательная технология. / .?М.: Народное образование, 2001.
4. Епишева обучения математике на основе деятельностного подхода: Кн. для учителя. / . ? М.: Просвещение, 2003.
5. Саранцев обучения математике на рубеже веков. // Математика в школе.? 2000.? № 7. ? С.2-5.
6. Методика и технология обучения математике. Курс лекций: пособие для вузов / под научн. ред. , . – М.: Дрофа, 2005.
Дополнительная литература
Методические особенности реализации интегративной технологии развивающего обучения на уроках математики различной целевой направленности в основной школе
Понятие развивающего обучения. Психолого-педагогические основы развивающего обучения. Анализ существующих концепций развивающего обучения.
Понятие технологии обучения. Интегративная технология развивающего обучения (организационный момент, актуализация знаний, постановка проблемы, «открытие» нового знания, первичное закрепление, самостоятельная работа с самопроверкой в классе, повторение, итог урока).
Опыт реализации российскими школами технологии развивающего обучения. Конструирование системы уроков по одному из разделов курса математики на основе технологии развивающего обучения. Реализация системы разработанных уроков в реальном учебном процессе, обоснование их эффективности.
Литература: [85], [101], [105], [115], [116], [138], [140], [143], [182], [184], [192], и учебно-методические пособия ассоциации «Школа 2000».
Дополнительная литература
Методические особенности реализации интегративной технологии развивающего обучения на уроках математики различной целевой направленности в 10-11 классах
Понятие технологии обучения. Интегративная технология развивающего обучения (организационный момент, актуализация знаний, постановка проблемы, «открытие» нового знания, первичное закрепление, самостоятельная работа с самопроверкой в классе, повторение, итог урока).
Опыт реализации российскими школами технологии развивающего обучения. Конструирование системы уроков по одному из разделов курса математики на основе технологии развивающего обучения. Реализация системы разработанных уроков в реальном учебном процессе, обоснование их эффективности.
Литература: [85], [101], [105], [115], [116], [138], [140], [143], [182], [184], [192], и учебно-методические пособия ассоциации «Школа 2000».
Дополнительная литература
Методическая система углубленного изучения математики в средней школе
Понятие о методической системе обучения. Психолого-педагогические основы методической системы углубленного изучения математики в средней школе. Понятие способные и одаренные дети. Психологические особенности способных и одаренных детей различных возрастных групп. Особенности обучения способных и одаренных детей.
Анализ опыта обучения способных и одаренных детей в отечественной и зарубежных школах. Обзор методических систем обучения математике способных и одаренных детей. Разработка системы уроков, факультативного курса одной из тем классов и школ с углубленным изучением математики. Апробация разработки. Анализ результатов.
Литература:
[1], [7], [10], [20], [27], [45], [47], [53], [55], [60], [61], [63], [79], [81], [82], [85] [97], [110], [114], [126], [139], [143], [165], [166], [172], [188], [204], [205],.[233], [274].
Дополнительная литература
Проверка и оценка знаний учащихся по математике
Понятие о проверке знаний учащихся. Цели и принципы организации проверки знаний по математике.
Виды проверки знаний учащихся по математике, примеры из различных математических курсов.
Проверка, контроль и оценка знаний учащихся (соотношение этих понятий).
Различные системы оценивания. Принципы отбора содержания для контроля знаний учащихся итоговый контроль.
Литература:
1. . Проверка знаний учащихся в средней школе. АПН РСФСР, М. 1960.
2. Вопросы проверки знаний, умений и навыков учащихся по предметам естественно-математического цикла.- М: 1978.
3. [193], [194].
Дополнительная литература
Обязательные результаты обучения и их роль в организации процесса обучения
Понятие об обязательных результатах обучения и принципах их разработки. Примеры обязательных результатов обучения (основная и старшая школа).
Виды обязательных результатов обучения и их функции на различных этапах обучения (примеры).
Методика подготовки и проведения различных типов уроков математики, реализующих основные функции ОРО.
Литература:
1. [224].
2. Теоретические основы определения требований к математической подготовке учащихся. М.: Ротапринт НИИ Общей педагогики, 1982.
3. Планируемые результаты обучения математике. М.: ротапринт СССР, 1984.
4. Обязательные результаты обучения математике. //Математика в школе– №3, №4.
Дополнительная литература
Тесты как средство контроля знаний учащихся по математике в условиях уровневой дифференциации обучения
Психолого-педагогические основы контроля знаний учащихся по математике.
Особенности организации и содержания контроля знаний в условиях уровневой дифференциации.
Тест и его особенности. Методические основы контроля знаний учащихся с помощью тестов в условиях уровневой дифференциации обучения математике.
Методическая разработка тестирования учащихся по одной из параллелей (5-11 классы). Апробация разработок. Анализ результатов.
Литература:
1. [4], [286].
2. «Психологическое тестирование». КН.1, М.: Педагогика.1982.
3. «Зачеты в системе дифференцированного обучения математике». М.: Просвещение. -1993.
4. «Контроль на уроках математики». Минск: Нар. асвета. -1986
5. «Конструирование тестов и методика их использования при контроле знаний учащихся по математике». М.: -1987.
6 «Тестирование как средство управления учебным процессом при обучении математике в специальных классах». М.: 1992
7. «Об использовании методов тестов при учете успеваемости школьников». М.: Сов. педагогикаЗ
8. , Пушкин СА и др. Сборник заданий тематических тестов для 6 класса по математике. М.: МИПКРО - 1999.
9. Краснянская КА. «Опыт применения избирательных тестов к изучению знаний учащихся по математике». М.: Сов. педагогика. -1965.
Дополнительная литература
Формирование культуры математического мышления учащихся
(на примере формирования и развития понятия математической модели
в школьном курсе математики)
Понятие "культура мышления". Понятие математической модели.
Основные задачи школьного математического образования:
– ознакомление учащихся с соотношениями между явлениями реального или проектируемого мира и его математическими моделями;
– формирование понимания учащимися роли абстрактной математической модели в осознании сути объектов и явлений;
– осознание учащимися необходимости приобретения умений для построения математических моделей.
Анализ действующих учебников в плане реализации указанных целей. Методические разработки.
Литература: [85], [115], [116], [117], [228], [229], [З06].
Дополнительная литература
Активизация самостоятельной деятельности учащихся по овладению новыми математическими знаниями
Психологические основы активизации самостоятельной деятельности учащихся. Активизация самостоятельной деятельности учащихся на уроках математики при изучении различных тем. Использование домашнего задания для активизации самостоятельной деятельности учащихся по овладению новыми знаниями.
Активизация самостоятельной деятельности учащихся в процессе выполнения учебно-исследовательских работ по математике.
Организация учебно-исследовательской деятельности учащихся. Примеры заданий для учащихся по выполнению самостоятельной учебно-исследовательской работы.
Разработка конкретного содержания домашнего задания с целью активизировать самостоятельную работу учащихся и методических рекомендаций по его выполнению для серии уроков при изучении различных тем (для одного из классов).
Литература: [31], [47], [55], [56], [85], [86], [103], [106], [114], [170], [211], [223], [304].
Дополнительная литература
Методика проведения уроков объяснения нового материала
(на примере подготовки уроков математики в основной или в старшей школе)
Дидактическая сущность уроков объяснения нового материала.
Структура урока объяснения нового материала. Принципы отбора содержания и методов его изложения. Средства обучения, методы организации первичного закрепления.
Мотивация изучения нового материала. Различные приёмы активизации деятельности учащихся при объяснении нового материала.
Практическая разработка, иллюстрирующая изучение какой-либо темы различными методами.
Литература: [254], [184], [186], [173], [106], [193], [194], [187], [283], [308].
Дополнительная литература: Черных, А. А. С чего начинается объяснение нового материала / // Математика в школе.–1984.– № 2.
Методика проведения уроков обобщения и систематизации знаний
Понятия обобщения и систематизации знаний (в широком смысле слова) в дидактике.
Виды обобщения знаний в методике математики.
Обобщение и систематизации знаний (математических понятий и способов деятельности) как необходимый этап обучения.
Примеры уроков обобщения и систематизации знаний по одной из тем курса математики.
Литература: [280], [186], [215], [254], [308], [184], [94].
Дополнительная литература: Наумова, Е. А. Систематизация стандартных знаний / // Математика в школе.– 1997.– № 1.
Суворова, М. В. Повторительно-обобщающие уроки в курсе математики / // Математика в школе. – 1995.– № 4.
Методика формирования математических понятий
Понятие. Объем и содержание понятия. Примеры понятий. Определение понятия, виды определений, примеры из школьных курсов алгебры и геометрии.
Этапы процесса формирования понятий (мотивация, выявление существенных признаков, формулировка, усвоение логической структуры, использование понятия). Разработка системы упражнений для формирования конкретного (по выбору студента) понятия курса математики. Разработка конкретных уроков по формированию понятий).
Литература: [254], [194], [193].
Дополнительная литература:
Методика подготовки к единому государственному экзамену
по математике
Контрольные измерительные материалы (КИМ) по математике и их особенности.
Характеристика содержания КИМ (кодификатор контролируемых элементов) и типов заданий. Особенности заданий с выбором ответа, с кратким ответом и с развёрнутым ответом.
Систематизации знаний и способов деятельности для выполнения заданий базового уровня сложности. Система упражнений для проверки усвоения.
Систематизации знаний и способов деятельности для выполнения заданий повышенного уровня сложности. Система упражнений для проверки усвоения.
Литература:
1. , , и др. Единый государственный экзамен 2009. Математика. Универсальные материалы для подготовки учащихся. /ФИПИ – М.: Интелект-Центр, 2009. – 272 с.
2. , , ёнов, ЕГЭ 2009. Математика: Сборник экзаменационных заданий./М.: ЭКСМО, 2009. – 288 с.
3. Кочагина, М. Н. ЕГЭ-2009. Математика. Репетитор / , .– М.: Эксмо, 2009.
4. Кочагина, М. Н. ЕГЭ-2009. Математика. Сборник заданий / , .– М.: Эксмо, 2009.
Дополнительная литература
Методика работы учителя математики в рамках информатизации процесса обучения
Концепция информатизации образования в России. Традиционные и новые средства обучения математике.
Современное оборудование кабинета математики (электронная доска, оверхэд…). Требования к оснащению кабинета математики.
Направления использования современных технических и информационно-коммуникативных средств обучения математике. Анализ программного обеспечения к электронным доскам различных видов для уроков математики.
Примеры использования современных технических и информационно-коммуникативных средств обучения математике и методические рекомендации по работе с ними.
Литература:
1. Новые педагогические и информационные технологии в системе образования / , , ; Под ред. ? М.: Академия, 2005.
2. Информационные и коммуникационные технологии в образовании: Учебно-методическое пособие / , , ; Под ред. .– М.: Дрофа, 2008.
3. Перечни учебной техники и наглядных средств обучения для общеобразовательной школы: Сб. перечней / Под ред. , Ю. С Песоцкого– М.: Педагогика, 2005.
4. 191-194.
Дополнительная литература
II. Частные методики
Основная школа
Преемственность в обучении математике
между начальной школой и основной
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические особенности обучения математике в начальной школе и в 5 классе с учетом возрастных особенностей учащихся. Анализ причин снижения успеваемости по математике при переходе учащихся на другую ступень обучения. Преемственность в методах и формах обучения
Развитие в 5 классе предметных знаний, умений и навыков, приобретенных учащимися в начальной школе.
Анализ программ и учебников по математике для начальной школы и 5 класса. Сравнительный анализ изложения итогового повторения в курсах (сравнительный анализ изложения определенной темы).
Разработка и описание методики проведения повторения материала по курсу математики начальной школы, в начале учебного года (или в течение учебного года при изучении определенной темы). Авторский вариант планирования, системы упражнений, контрольных материалов.
Литература:
1.Учебники и программы по математике Федерального перечня для начальной школы.
2.Атаханов. Р. Системы начального обучения: учебники по математике и математическое образование учащихся// Педагогика,2000, №1. С. 40-47.
3.Волошкина познавательной деятельности младших школьников на уроках математики. // Начальная школа. – 1992. - № 9/10. – С. 15-18.
4.Еланская познавательной деятельности младших школьников на уроках математики. // Начальная школа. – 2001. - № 6. – С.52.
5.Жохов математики в 5-6 классах. М.: Вербум-М, 2000.
6.Истомина обучения математики в начальных классах.- М. 6 Линка - Пресс, 1998г.
7. Матющенко ликвидировать «ножницы» в математическом образовании при переходе учащихся из 4 в 5 класс. // Начальная школа, 200, № 6,- С. 54.
Дополнительная литература
Решение логических задач на уроках математики в 5-6 классах
Роль логических задач в обучении математике. Представление о логических задачах. Различные типы логических задач и методы их решения.
Анализ учебников математики 5-6-х классов и оценка состава логических задач в рассмотренных учебниках. Обучение решению логических задач: методы и приемы. Система логических задач в 5-6-х классах.
Литература: [23], [26], [113], [149], [157], [175], [194], [198], [212], [232], [336], учебники математики для 5-6 классов из Федерального перечня.
Дополнительная литература
Методика формирования эвристических приемов
на уроках математики в 5-6 классах
Эвристика. Значение эвристического мышления для развития личности. Эвристические приемы. Анализ учебников математики 5-6-х классов с целью выявления возможных эвристических приемов решения задач.
Конкретные рекомендации по организации обучения, нацеленного на формирование эвристических приемов. Система задач и упражнений, позволяющих формировать эвристические приемы.
Литература: [130], [134], [166], [194], [2ЗО], [240], [З06], учебники математики для 5-6 классов из Федерального перечня.
Дополнительная литература
Реализация принципа ведущей роли теоретических знаний в обучении
(на примере изучения алгоритмов действий в курсе математики 5-6 классов)
Традиционная и развивающая системы обучения.
Здоровьесберегающие технологии обучения.
Образовательное пространство развивающего типа, его характерные черты. "Школа памяти" и "школа развития", их различие. Принципы развивающего обучения в начальной школе по (краткая характеристика).
Основной принцип развивающего обучения – принцип ведущей роли теоретических знаний. Суть этого принципа – осознанное усвоение новых знаний учащимися, Т. е. осознание необходимости введения новых понятий и их сути, осознание новых алгоритмов действий. Сравнение с трактовкой ведущей роли теоретических знаний в обучении. Сравнение принципа ведущей роли теоретических знаний и hpинципа сознательности в обучении.
Сравнительный анализ учебников традиционного и инновационного направлений в плане реализации возможности сознательного (в смысле "осознанного") усвоения теоретических знаний учащимися при изучении алгоритмов действий в 5-6 классах по следующему плану:
– расширение представлений учащихся о различных способах записи натуральных чисел, о преимуществах десятичной системы счисления и позиционного способа записи чисел, использование с этой целью таблицы разрядов;
– использование позиционного способа записи чисел при выполнении арифметических действий с натуральными числами;
– введение понятия обыкновенной дроби как частного от деления натуральных чисел и как одной или нескольких равных долей единицы;
– обоснование алгоритмов действий с обыкновенными дробями;
– введение понятия десятичной дроби;
– обоснование алгоритмов действий с десятичными дробями;
– введение понятий "отрицательное число", "положительное число";
– обоснование алгоритмов действий с положительными и отрицательными числами.
Выводы и предложения.
Литература:
[85], [228], [229], учебники Федерального перечня по математике для 5-6 классов.
Дополнительная литература
Организация поисково-эвристической деятельности учащихся на уроках
(на примере изучения материала геометрической линии курса математики 5-6 классов)
Поисково-эвристическая деятельность – необходимое условие формирования и развития мышления.
Цели изучения геометрии в школе. Пропедевтический характер геометрического материала курса математики 5-6 классов.
Методика изучения геометрического материала в 5-6 классах:
o элементы геометрии в начальной школе (сравнительный анализ учебников федерального комплекта для начальной школы);
o требования к математической подготовке учащихся в плане изучения геометрических понятий и их свойств в курсе математики 5-6 классов (что учащиеся должны знать, уметь, какие навыки должны быть сформированы, какие понятия должны быть усвоены на уровне представлений);
o последовательность изучения геометрического материала в 5-6 классах;
o требования к уровню корректности определений и обоснований свойств геометрических понятий в 5-6 классах (2-3 примера).
Сравнительный анализ действующих учебников математики для 5-6 классов по следующим направлениям:
o наличие системы упражнений, подводящих учащихся к введению того или иного понятия, позволяющих учащимся выдвинуть гипотезу о каком-либо свойстве того или иного понятия (примеры);
o формирование в сознании учащихся понимания того, что вывод, сделанный ими в результате наблюдений - это (в большинстве случаев) гипотеза, формирование понимания необходимости обоснования выдвинутых гипотез.
Примеры организации поисково-эвристической деятельности учащихся (сценарии уроков, фрагментов уроков).
Выводы и предложения.
Литература: [85], [115], [116], [117], [123], [228], [229], [324], учебники Федерального перечня по математике для 5-6 классов.
Дополнительная литература
Управление проблемно-поисковой и исследовательской деятельностью учащихся на уроках математики (на примере изучения алгоритмов действий с обыкновенными и десятичными дробями)
Значение проблемного подхода в обучении для создания образовательного пространства развивающего типа. Реализация проблемного подхода в обучении при изложении теоретического материала в действующих учебниках (сравнительный анализ). Методика изучения алгоритмов действий с обыкновенными и десятичными дробями.
Литература: [85], [115], [116], [117], [123], [184], [228], [229], [258], учебники Федерального перечня по математике для 5-6 классов.
Дополнительная литература
Педагогические идеи Д. Пойа при обучении учащихся решению арифметических задач на уроках математики в 5-6-м классах
Анализ основных педагогических идей Д. Пойа. Выявление обобщенных подходов, сформулированных в работах Д. Пойа.
Понятие задачи и арифметические методы решения задач. Анализ учебников математики 5-6-х классов на предмет использования идей Д. Пойа при обучении решению задач.
Разработка материалов с методическими рекомендациями по их использованию на уроках математики в 5-6-м классах.
Литература: [19], [85], [228], [229], [230], [231], [238], [264], [304], [307], [308], [309], [310], [311], [325].
Дополнительная литература
Использование исторического материала в развитии познавательного интереса на уроках математики в 5-6-х классах
Психолого-педагогические основы преподавания математики в 5-6-х классах. Методы и формы активизации познавательного интереса учащихся 5-6-х классов. Развитие интереса к математике через знакомство с историей науки и историческими задачами. Требования к содержанию и формам изложения исторических сведений.
Анализ литературы, содержащей старинные задачи, материал по истории математики, и учебного материала, содержащегося в учебниках математики 5-6-х классах на предмет возможности использования математического наследия на уроках математики.
Методические рекомендации по рассмотрению исторического материала, старинных задач на уроках математики. Разработка занятий по конкретным темам курса математики 5-6-го класса.
Литература:[15], [19], [28], [72], [73], [74], [78], [85], [98], [164], [227], [232], [246], [264], [304], [307], [308], [309], [311], [324], [328].
Дополнительная литература
Система упражнений, направленных на развитие пространственных представлений учащихся 5-6 классов
Психолого-педагогические основы .развития. пространственных представлений учащихся 5-6 классов. Визуальное и логическое мышление учащихся 5-6 классов.
Роль упражнений в развитии пространственных представлений учащихся.
Типология упражнений.
Методическая разработка системы упражнений. Апробация материалов. Анализ результатов.
Литература: [9], [11], [13], [19], [24], [25], [50], [64], [80], [109], [112], [124], [149], [161], [174], [185], [211], [234], [237], [254], [265], [278], [288], [305], [315], [316], [328], [341], [342].
Дополнительная литература
Формирование комбинаторного мышления учащихся на уроках математики в 5-6 классах
Понятие комбинаторного мышления. Значение комбинаторного мышления для успешной практической деятельности человека и успешного обучения в школе.
Анализ программ, учебников и учебных пособий (действующих; советского периода; в зарубежных школах) на предмет выявления в них элементов комбинаторных знаний и возможности на их базе формирования комбинаторного мышления (акцент анализа делается для возрастной группы 11-12 лет).
Типология задач и упражнений, обеспечивающих формирование комбинаторного мышления.
Разработка системы задач и упражнений (можно - дополняющей систему упражнений. одного из. действующиХ. учебников), ориентированной на. формирование. комбинаторного. мышления учащихся 5-6 классов.
Проверка эффективности. разработанной .системы задач. и упражнений в реальном учебном процессе.
Литература: [4], [36], [44], [52], [134], [154], [165], [188], [204], [225], [233], [244], [256], [287], [289], [292], [293], [294], [313], [320], {321].
Дополнительная литература
Использование цифровых образовательных ресурсов на уроках математики в 5-6 классах
Анализ психолого-педагогической литературы, посвященной проблемам использования компьютера в школе.
Анализ существующих цифровых образовательных ресурсов (ЦОР) в плане эффективности их использования в процессе обучение математике.
Самостоятельная разработка ЦОР с использованием существующих программных средств. Описание методики изучения одной темы школьного курса математики 5-6 классов с использованием компьютерных технологий.
Литература:
1) Григорьев, С. Г. Учебник «Информатизация образования. Фундаментальные основы». [Электронный документ] / , . – (http://www. *****/download. php? id=455
2) Гриншкун, В. В. Информатизация образования как направление подготовки педагогов [Электронный документ] / – (http://www. *****/download. php? id=451
3) Зайцева, С. А. Современные информационные технологии в образовании. [Электронный документ] , . – (http://*****/infotek/infotek2.htm). 25.01.2009.
4) Зубарева, И. И. Методические рекомендации по использованию цифровых образовательных ресурсов к учебнику «Математика, 5 класс» авторов , [Электронный документ]/ , . – (http://school-collection. *****) 25.01.2009.
5) Зубарева, И. И. Методические рекомендации по использованию цифровых образовательных ресурсов к учебнику «Математика, 6 класс» авторов , [Электронный документ]/ , . – http://school-collection. ***** . 25.01.2009.
6) Каталог образовательных ресурсов сети Интернет [Электронный документ] / . – (http://katalog. *****/index. php? id=
7) Куклина, Е. О. Проектная технология в рамках организации работы с интерактивной доской. Методическое пособие по работе с интерактивной доской ACTIVboard в учебном кабинете [Электронный документ] / . – (http://www. *****/io/3/kuklina). 25.01.2009.
8) Савченко, Н. А. Использование информационных и коммуникационных технологий в общем среднем образовании [Электронный документ] / . – (http://www. humanities. *****/db/msg/80297/). 25.01.2009.
9) Филиппов, В. М. "Учебный курс «Тенденции и формы использования информационных и коммуникационных технологий в трансграничном образовании» в системе повышения квалификации работников образовательных учреждений". [Электронный документ] / , , . –(http://www. *****/download. php? id=451
10) Худякова, О. И. Построение графика квадратичной функции (математика, 8 клаcc) [Электронный документ] / (http://www. *****/io/3/khudiakova/). 25.01.2009
11) Новые педагогические и информационные технологии в системе образования / , , ; Под ред. ? М.: Академия, 2005.
12) Информационные и коммуникационные технологии в образовании: Учебно-методическое пособие / , , ; Под ред. .– М.: Дрофа, 2008.
Использование компьютерных средств
на уроках математики 5-6 классов
(при изучении геометрического материала)
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания математики в 5-6 классах. Средства обучения математики. Компьютерные средства обучения математики и их возможности для повышения эффективности процесса обучения. Организация процесса обучения в 5-6 классах с применением компьютерных средств
Сравнительный анализ современных компьютерных средств для курса математики 5-6 классов.
Особенности содержания геометрического материала курса математики 5-6 классов. Методики изучения геометрического материала с применением компьютерных средств.
Авторский вариант разработки системы уроков, иллюстрирующих предложенную методику.
Литература:
1.Учебники и программы Федерального перечня по математике 5-6 классов.
3.Жохов математики в 5-6 классах. М.: Вербум-М, 2000
4. Мартиросян рекомендации к комплексному использованию электронных средств учебного назначения в процессе обучения математики ( на примере 5-6 классов)/ – М.: ИИО РАО, 2006.
5. Мартиросян. геометрия на уроках математики// Информатика и образование - 2005.-№:.- С.77-79.
Дополнительная литература
Текстовые задачи в курсе алгебры основной школы
Психолого-педагогические основы обучения решению текстовых задач учащихся 7-9 классов.
Роль и место текстовых задач в курсе алгебры 7-9 классов. Типология текстовых задач.
Этапы обучения решению текстовых задач в основной школе. Методы решения текстовых задач в основной школе. Особенности методики обучения решению текстовых задач в основной школе.
Методическая разработка по одному из этапов.
Апробация разработки. Анализ результатов.
Литература: [63], [118], [127], [130], [144], [149], [151], [164], [173], [183], [189], [198], [212], [224], [230], [279], [296], [304], [309], [311].
Дополнительная литература
Уравнения и неравенства с параметром как средство формирования исследовательских умений учащихся в условиях уровневой дифференциации обучения по курсу алгебры
в 7-9 классах (или в 10-11 классах)
Психолого-педагогические основы формирования и развития. исследовательских умений учащихся в. условиях уровневой дифференциации. Дидактический анализ исследовательской деятельности.
Этапы обучения решению параметрических уравнений инеравенств.
Роль и место параметрических уравнений и неравенств в курсе алгебры. Методы решения параметрических уравнений инеравенств.
Методическая разработка цикла упражнений, направленных на формирование и развитие исследовательских умений учащихся.
Литература: [7], [63], [82], [83], [85], [95], [102], [106], [127], [129], [163], [166], [173], [213], [223], [224], [240], [241], [246], [254], [343].
Дополнительная литература
Методика обучения решению уравнений с параметрами на уроках алгебры основной школы
Понятие уравнения с параметрами. Место и роль уравнений с параметрами в процессе обучения математике. Основные методы решения уравнений с параметрами.
Анализ учебников алгебры на предмет выявления возможности организации обучения решению уравнений с параметрами при изучении различных видов уравнений: линейных; квадратных; дробно-рациональных; уравнений, содержащих выражение под знаком модуля. Особенности методики обучения решению уравнений с параметрами в основной школе.
Пример системы заданий для обучения решению уравнений с параметрами по темам курса математики основной школы.
Литература: [7], [63], [82], [83], [172], [183], [194], [224], [238], [252], [254], [323], [343].
Дополнительная литература
Изучение элементов стохастики в 7-9 классах общеобразовательной школы
Понятие стохастики. Общекультурное значение стохастических знаний. Стохастический стиль мышления.
Изучение элементов стохастики в зарубежных школах. Исторический опыт российских школ включения вопросов комбинаторики, вероятностей и статистики в содержание общеобразовательных программ по математике, в содержание факультативных курсов.
Современное состояние изучения вопросов стохастики в 7-9 классах отечественной школы. Анализ стохастической линии в действующих учебниках математики.
Методика изучения элементов стохастики в основной школе. Конструирование системы уроков по одному из разделов стохастической линии содержания в 7-9 классах. Проверка эффективности разработанной методики на практике.
Литература: [4], [10], [35], [44], [52], [54], [76], [77], [134], [148], [154], [165], [181], [188], [204], [225], [233], [244], [273], [287], [289], [290], [291], [294], [302], [303], [31 3], [320], [321], [334].
Дополнительная литература
Усвоение курса математики основной школы в условиях индивидуального обучения школьников
Психология усвоения знаний детьми подросткового возраста.
Понятие педагогической коррекции. Педагогическая коррекция математических знаний школьников на разных возрастных этапах, при различных причинах отставания, при разной степени «запущенности».
Особенности индивидуального обучения математике в домашних условиях (в сочетании с посещением им школьных занятий и без таковых).
Понятие репетитора в современной педагогике. Роль репетитора по математике в условиях индивидуального обучения ребенка.
Разработка форм, средств и методов обучения математике подростка, нуждающегося в индивидуальном коррекционном обучении (в условиях дифференциации причин и уровня отставания от программных требований).
Практическаяреализация и проверка эффективности разработанного методического аппарата в процессе обучения математики конкретных детей.
Литература: [4], [16], [28], [31], [60], [65], [80], [81], [99], [103], [114], [134], [142], [143], [154], [165], [169], [172], [174], [177], [178], [179], [180], [188], [204], [216], [218], [220], [233], [237], [244], [251], [256], [285], [288], [291], [292], [293], [311], [314], [316], [340].
Дополнительная литература
Возможности развития пространственного мышления учащихся основной школы
Понятие пространственного мышления. Психологические основы формирования пространственного мышления детей на разных возрастных этапах.
Анализ действующих программ, учебников и учебных пособий для основной школы на предмет выявления возможности на их основе формирования пространственного мышления у детей.
Методика формирования пространственного мышления учащихся на уроках математики (либо в 5-6 классах, либо в 7-9 классах).
Реализация разработанной методики в реальном учебном процессе, обоснование ее эффективности.
Литература: [4], [9], [11], [25], [33], [50], [60], [64], [65], [75], [88], [109], [124], [133], [134], [161], [174], [176], [185], [206], [218], [234], [237], [244], [278], [288], [305], [316], [328], [340], [341], [342].
Дополнительная литература
Использование дополнительных построений при решении геометрических задач в курсе планиметрии
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания геометрии в 7-9 классах с учетом возрастных особенностей учащихся.
Анализ имеющейся учебной и методической литературы по теме.
Теоретические основы метода дополнительных построений.
Классификация дополнительных построений. Взаимосвязь метода дополнительных построений с другими методами.
Разработка методики формирования умения использовать дополнительные построения, в частности использование геометрических фактов, лежащих в основе дополнительных построений.
Подбор и классификация задач, решаемых с использованием данного метода.
Выводы.
Литература: [60], [61], [85], [112], [195], [296], [271], [308].
Дополнительная литература
Методика изучения геометрических преобразований
в курсе планиметрии
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания геометрии в 7-9 классах с учетом возрастных особенностей учащихся.
Теоретические основы геометрических преобразований.
Анализ материала, представленного по данной теме в учебнике «Геометрия 7-9» федерального комплекта различных авторских коллективов.
Методы, основанные на геометрических преобразованиях, и их теоретические основы.
Разработка методики изучения геометрических преобразований, представленных в курсе планиметрии: движения (виды движений: поворот, параллельный перенос, осевая симметрия), подобия, в частности гомотетии. Применение метода геометрических преобразований.
Конструирование групп уроков, подбор и систематизация задач.
Выводы, подтверждающие целесообразность проделанного исследования.
Литература: [12], [30], [61], [65], [83], [195], [225], [308].
Дополнительная литература
Методика обучения основным методам решения задач на построение
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания геометрии в 7-9 классах с учетом возрастных особенностей учащихся.
Анализ материала, представленного по данной теме в учебнике «Геометрия 7-9» федерального комплекта различных авторских коллективов.
Теоретические основы методов решения задач на построение.
Разработка методики изучения методов геометрических построений, представленных в курсе планиметрии: метод геометрических мест точек, метод геометрических преобразований, алгебраический метод.
Конструирование групп уроков, подбор и систематизация задач по методам решения
Выводы.
Литература: [6], [12], [14], [60], [61], [85], [120], [162], [195], [196], [206], [271], [308].
Дополнительная литература
Формирование приемов умственной деятельности при решении геометрических задач
Анализ психолого-педагогической литературы по теме исследования; особенности умственной деятельности на уроках математики; психологопедагогические основы преподавания геометрии в 7-11 классах с учетом возрастных особенностей учащихся.
Анализ имеющейся учебной и методической литературы по теме.
Теоретические основы. Эвристические приемы: аналогия, обобщение, конкретизация и изучение их реализации при решении геометрических задач.
Методика организации поиска решения задачи на уроке.
Систематизация методов решения геометрических задач (алгебраический, векторный, координатный, метод геометрических преобразований, метод равных и подобных треугольников, метод площадей) в соответствии с эвристическими приемами.
Подбор и систематизация задач по эвристическим приемам.
Выводы.
Литература: [4], [19], [47], [55], [60], [61], [66], [87], [97], [127], [130], [134], [161], [165], [195], [196], [241], [308].
Дополнительная литература
Старшая школа.
Методика обучения нестандартным методам решения задач
по алгебре
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания математики в 10-11 классах с учетом возрастных особенностей учащихся.
Анализ имеющейся учебной и методической литературы по теме.
Роль и место нестандартных задач и нестандартных методов решения в системе курса алгебры средней школы.
Анализ материала, содержащегося в учебниках «Алгебра 10-11» федерального комплекта различных авторских коллективов, и отбор тем, оптимальных для применения при решении задач нестандартных методов.
Систематизация нестандартных методов решения: метод функциональной и тригонометрической подстановок, методы решения функциональных уравнений, векторный метод, методы на основе свойств функций.
Разработка методики обучения решению задач нестандартными методами, позволяющей научить учащихся диагностировать нестандартную задачу и метод ее решения.
Конструирование групп уроков.
Подбор и систематизация задач, решаемых нестандартными методами.
Выводы.
Литература: [19], [20], [45], [60], [61], [87], [165], [195], [196], [213], [241], [282], [308].
Дополнительная литература
Методика обучения построению чертежа
к стереометрической задаче
Пространственные представления учащихся и их формирование при обучении геометрии в старших классах.
Особенности решения стереометрических задач. Классификация задач.
Построение чертежа как этап решения задачи.
Изображение фигур в курсе геометрии старшей школы. Требования к изображению. Изображения многогранников, тел вращения и их комбинаций.
Умение «читать чертеж» и умение «изображать фигуру» при решении геометрической задачи.
Обучение изображению многогранников, тел вращения и их комбинаций в классах разных профилей.
Практическая часть состоит в составлении методических рекомендаций, разработке фрагментов уроков и системы упражнений.
Литература: 252, 253, 25, 237, 270, 278, 342, учебники Федерального перечня для старшей профильной школы по геометрии.
Дополнительная литература
Методика изучения одной из содержательных линий школьного курса математики с использованием ИКТ
Методические особенности изучения содержательной линии школьного курса математики (роль и место линии, установление внутрипредметных связей, последовательность изучаемых вопросов и их взаимосвязь и т. д.).
Методика проведения урока математики с использованием информационно-коммуникационных технологий.
Отбор электронных образовательных ресурсов (ЭОР) на CD-дисках для изучения выбранной содержательной линии школьного курса математики и их методический анализ.
Примеры составления собственных ЭОР для изучения выбранной содержательной линии школьного курса математики.
Практическая часть состоит в составлении методических рекомендаций, разработке ЭОР, фрагментов уроков и системы упражнений.
Литература:
1. Новые педагогические и информационные технологии в системе образования / , , ; Под ред. ? М.: Академия, 2005.
2. Методика и технология обучения математике. Курс лекций: пособие для вузов / под научн. ред. , .– М.: Дрофа, 2005.
3. Информационные и коммуникационные технологии в образовании: Учебно-методическое пособие / , , ; Под ред. .– М.: Дрофа, 2008.
Дополнительная литература
Методика изучения элементов математического анализа в классах гуманитарного профиля
История развития профильной дифференциации в отечественной школе: гуманитарный профиль и его особенности в русской школе начала ХХ века; профильная дифференциация в современной школе.
Психологические особенности подростков, склонных к деятельности в гуманитарной сфере.
Методика изучения выбранной темы в классах гуманитарного профиля: цели обучения, отбор содержания теоретического и задачногo материала, выбор средств, методов и форм обучения.
Анализ программ и учебников по математике для гуманитарных классов. Сравнительный анализ изложения конкретной темы в учебниках для гуманитарных классов и учебниках по алгебре и началам анализа для общеобразовательных учреждений.
Практическое приложение в виде конспектов уроков или системы упражнений для формирования понятий выбранной темы.
Литература: [3], [21], [28], [34], [38], [39], [48], [53], [61], [81], [86], [104], [129], [143], [150], [155], [170], [248].
Дополнительная литература
Методика изучения элементарных функций в классах гуманитарного профиля
История изучения элементарных функций в отечественной школе.
Современные модели профильной дифференциации обучения.
Особенности психологии подростков, склонных к деятельности в гуманитарной сфере. Роль наглядности при изучении теоретического материала.
Анализ содержания программ и требований стандартов по вопросам изучения элементарных функций. Цели изучения элементарных функций в гуманитарных классах.
Анализ учебников для гуманитарных классов по математике. Возможности использования учебников для общеобразовательных школ при работе в классах гуманитарного профиля в ходе изучения элементарных функций. Особенности изучения теоретического и задачноro материала. Формирование умений при менять знание свойств элементарных функций на практике.
Авторский вариант методических рекомендаций изучения элементарных функций в гуманитарных классах (на примере изучения свойств одной из функций).
Литература: [3], [21], [28], [34], [38], [39], [41], [48], [49], [53], [61], [81], [86], [104], [129], [143], [155], [170], [248], [266].
Дополнительная литература
Роль и место задач в обучении математике учащихся классов гуманитарного профиля
Об изучении математики через задачи в русской классической гимназии начала ХХ века. Спектр практических навыков по математике в классах гуманитарного профиля зарубежной школы.
Особенности психологии подростков, склонных к деятельности в гуманитарной сфере
Функции задач в обучении математике учащихся классов гуманитарного профиля. Повышение интереса к математике, в частности, через систему задач и упражнений. Нетрадиционные формы заданий для классной и домашней работы учащихся гуманитарных классов.
Сравнительный анализ систем упражнений в учебниках математики для гуманитариев и для учащихся общеобразовательных школ. Анализ заданий для подготовки и проведения письменного экзамена по математике за курс средней школы. Возможности использования учебников для гуманитариев для подготовки к выпускным экзаменам.
Авторский вариант системы задач, упражнений и творческих заданий для изучения выбранной темы учащимися гуманитарных классов.
Литература: [15], [18], [21], [28], [38], [39], [41], [48], [49], [61], [65], [66], [81], [86], [104], [129], [143], [149], [150], [232], [233].
Дополнительная литература
Роль и место задач в обучении математике учащихся классов технического (экономического, естественнонаучного) профиля
Изучение математики в реальных училищах России начала ХХ века.
Практическая составляющая математического образования в зарубежной школе для профилей, в которых математика является аппаратом для изучения соответствующей сферы деятельности.
Особенности психологии подростков, склонных к деятельности в технической сфере.
Специальные функции задач в обучении математике учащихся классов, выбирающих в качестве будущей сферы деятельности ту, в которой математика является аппаратом для овладения умениями действовать в выбранной сфере. Роль практических и прикладных задач в обучении математике учащихся профильных классов. Возможности реализации меж предметных связей при решении задач учащимися профильных классов.
Анализ программ и стандартов для профильной отечественной школы. Сравнительный анализ системы упражнений по выбранной теме в различных учебниках алгебры и начал анализа для общеобразовательной школы. Анализ заданий для подготовки и проведения письменного экзамена по математике за курс средней школы. Рекомендации по использованию конкретных учебников для работы в классах определенного профиля.
Авторский вариант системы задач по изучению выбранной темы в классах конкретного профиля.
Литература: [18], [21], [29], [42], [61], [65], [66], [81], [86], [104], [129], [147], [149], [150], [152], [153], [209], [229], [304].
Дополнительная литература
Изучение комбинаторики в 10-11 классах общеобразовательной и профильной школ
Комбинаторика как раздел математики, ее предмет и содержание.
Традиции изучения элементов комбинаторики в отечественной и зарубежной школе.
Современное состояние вопроса включения комбинаторных знаний в отечественные программы и учебники по математике, в частности, для старшей (общеобразовательной и профильной) школы.
Характеристика психологических особенностей учащихся, ориентированных на тот или иной профиль обучения.
Возможности и необходимость дифференциации комбинаторных знаний в зависимости от профиля обучения.
Методика изучения вопросов комбинаторики на одном из профилей обучения (возможно - в приложении к содержанию одного из учебников для профильной или общеобразовательной школы).
Конструирование и проведение уроков с использованием разработанной методики.
Литература: [4, [10], [28], [35], [36], [44], [52], [54], [60], [65], [76], [77], [81], [134], [148], [152], [153], [165], [172], [181], [188], [204], [225], [233], [244], [273], [285], [287], [294], [313], [320], [321], [334].
Дополнительная литература
Изучение элементов теории вероятностей в 10-11 классах общеобразовательной и профильной школ
Теория вероятностей как раздел математики, ее предмет и содержание. Традиции изучения элементов теории вероятностей в отечественной и зарубежной школе.
Современное состояние вопроса включения вероятностных знаний в отечественные программы и учебники, в частности, в содержание математического образования старшей (общеобразовательной или профильной) школы.
Характеристика психологический особенностей учащихся, ориентированных на тот или иной профиль обучения.
Необходимость и возможности дифференциации вероятностных знаний в зависимости от профиля обучения.
Методика изучения элементов теории вероятностей на одном из профилей обучения (возможно - в приложении к содержанию одного из учебников для профильной или общеобразовательной школы).
Конструирование и проведение уроков математики по рассматриваемой теме на основе разработанной методики.
Литература: [10], [28], [35], [44], [52], [54], [60], [65], [76], [77], [81], [134], [148], [152], [153], [172], [181], [225], [273], [285], [302], [303], [313], [320], [321], [334].
Дополнительная литература
Изучение элементов математической статистики в 10-11 классах общеобразовательной и профильной школ
Математическая статистика как раздел математики, ее предмет и содержание, связь с теорией вероятностей.
Традиции изучения элементов статистики в отечественной и зарубежной школе.
Современное состояние вопроса включения статистических знаний в отечественные программы и учебники, в частности, в программы и учебники для старшей (общеобразовательной и профильной) школы.
Характеристика психологических особенностей учащихся, ориентированных на тот или иной профиль обучения.
Необходимость и возможности дифференциации статистических знаний в зависимости от профиля обучения прикладные особенности статистических знаний для учащихся различных профилей.
Методика изучения элементов математической статистики на одном из профилей обучения (возможно - в приложении к содержанию одного из учебников математики для общеобразовательной или профильной школы).
Конструирование и проведение уроков по изучению элементов статистики на основе разработанной методики.
Литература: [4], [10], [28], [33], [36], [44], [52], [54], [60], [65], [76], [77], [81], [134], [148], [152], [153], [165], [172], [181], [188], [204], [225], [23З] , [244], [273], [285], [287], [294], [302], [ЗОЗ], [З13], [320], [321], [З34].
Дополнительная литература
Методика изучения делимости чисел в профильных классах
История изучение делимости чисел в отечественной школе: в России начала ХХ века и в советской школе.
Анализ программ и учебников по математике для 5-6 классов как пропедевтики изучения делимости чисел в старшей школе.
Анализ стандарта математического образования по данной теме и его реализации в существующих учебниках математики для профильной школы.
Представление о теории чисел через изучение делимости суммы и произведения, деления с остатком, признаков делимости, сравнений.
Методические особенности изучения одного из разделов темы в профильных классах.
Литература
Основная литература.
1. Голубева . Личность. Индивидуальность. - Дубна, Феникс, 2005. – 512 с.
2. Гусев -педагогические основы обучения математике. - М.: «Вербум-М», центр «Академия», 2003.
3. Епишева обучения математике на основе деятельностного подхода. – М.: Просвещение, 2004.
4. Ильин индивидуальных различий. – С. Петербург, Питер, 2004. – 701 с.
5. Колягин школа и математическое образование: Наша гордость и наша боль. – М.: Просвещение, 2004.-318 с.
6. , , ; под ред. Жижченко и начала математического анализа : учеб. Для 10 кл. общеобразоват. учреждений : базовый и профил. уровни. – М.: Просвещение, 2008. – 368 с.
7. , , ; под ред. Жижченко и начала математического анализа : учеб. Для 11 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2009. – 398 с.
8. Крымова проектов в обучении математике. \\«Математика в школе», 2006, №4, с.62.
9. Методика и технология обучения математике. Курс лекций: пособие для вузов \ под научн. ред. , . – М.: Дрофа, 20с.
10. , Семенов и начала анализа. 10 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений (профильный уровень)- М.: Мнемозина, 2007. – 424 с.
11. , Семенов и начала анализа. 11 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений (профильный уровень)- М.: Мнемозина, 2007. – 287 с.
12. , Семенов и начала анализа. 10 класс. (профильный уровень). Методическое пособие для учителя - М.: Мнемозина, 2008.
13. «Преподавание математики и новые компьютерные технологии» \\ «Математика в школе»,2005, №6, с.73; №7, с.56.
14. , , Шевкин и начала анализа: Учеб. Для 10 кл. общеобразоват. учреждений.- М.: Просвещение, 2008, - 383 с.
15. , , Шевкин и начала анализа: Учеб. Для 11 кл. общеобразоват. учреждений.- М.: Просвещение, 2008, - 448 с.
16. Саранцев обучения математике в средней школе: учебное пособие для студентов мат. спец. пед. вузов и ун-тов – М.: Просвещение, 2005. – 224 с.
17. Сборник нормативных документов. Математика/ сост. , .- М.: Дрофа, 20с.
18. , Ткачева алгебры и начал математического анализа в 10 классе: кн. Для учителя. – М.: Просвещение, 2008. – 190 с.
19. О прикладной ориентации курса математики \\ «Математика в школе», 2007, №6, с.2; №7, с.2.
20. Фридман основы методики обучения математике: Учебное пособие. –М.: Едиториал УРСС, 2005.-248 с.
21. Фридман научиться решать задачи: Кн. для учащихся 10-11 классов. – М.: Просвещение,2004.
22. Юнина качественного обучения в школе. Учебно-методическое пособие – М.: Педагогическое общество России, 20с.
23. . Психологические основы математического образования: Учеб. Пособие для студ. Пед. Вузов – М.: Издательский центр «Академия». -2004, -320 с.
Дополнительная литература.
1. Башмаков и профиль школьного математического образования // Математика в школе№ 2.
2. Математика и математическое образование в современном мире. - М.: Просвещение, 1985.
3. Изюмова мнемических способностей и дифференциация обучения. – М.: Наука, 1995, - 382 с.
4. Концепция профильного обучения на старшей ступени общего образования // Вестник образования. – 2002. – декабрь № 4.
5. Концепция модернизации российского образования на период до 2010 года // Вестник образования. – 2002. –№ 6. – с. 11-40.
6. Унт Инге. Индивидуализация и дифференциация обучения. - М.: Педагогика, 1990.
7. Фридман -педагогические основы обучения математике в школе. - М.: Просвещение, 1983.
Методика изучения теории многочленов в профильной школе
Роль и место теории многочленов в изучении алгебры на разных этапах развития среднего образования в отечественной школе.
Анализ программ и учебников по алгебре для 7-9 классов как пропедевтики изучения многочленов в старшей школе.
Анализ стандарта математического образования по данной теме и его реализации в существующих учебниках математики для профильной школы.
Формирование понятия многочлена n –ой степени от одной переменной и нескольких переменных.. Обобщение и систематизация знаний учащихся об операциях над многочленами. Возведение двучленов в степень. Бином Ньютона. Симметрические многочлены Обучение решению алгебраических уравнений в основной и средней школе.
Конструирование уроков по теме с использованием компьютерных технологий.
Литература
Основная литература.
1.Голубева . Личность. Индивидуальность. - Дубна, Феникс, 2005. – 512 с.
2.Епишева обучения математике на основе деятельностного подхода. – М.: Просвещение, 2004.
3.Жафяров обучение математике старшеклассников. Учебно-дидактический комплекс.-Новосибирск: Сиб. унив. изд-во, 20с.
4.Ильин индивидуальных различий. – С. Петербург, Питер, 2004. – 701 с.
5.Колягин школа и математическое образование: Наша гордость и наша боль. – М.: Просвещение, 2004.-318 с.
6., , ; под ред. Жижченко и начала математического анализа : учеб. Для 10 кл. общеобразоват. учреждений : базовый и профил. уровни. – М.: Просвещение, 2008. – 368 с.
7., , ; под ред. Жижченко и начала математического анализа : учеб. Для 11 кл. общеобразоват. учреждений : базовый и профил. уровни. – М.: Просвещение, 2009. – 398 с.
8.Крымова проектов в обучении математике. \\«Математика в школе», 2006, №4, с.62.
9.Методика и технология обучения математике. Курс лекций: пособие для вузов \ под научн. ред. , . – М.: Дрофа, 20с.
10. , Семенов и начала анализа. 10 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений (профильный уровень)- М.: Мнемозина, 2007. – 424 с.
11., Семенов и начала анализа. 11 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений (профильный уровень)- М.: Мнемозина, 2007. – 287 с.
12., Семенов и начала анализа. 10 класс. (профильный уровень). Методическое пособие для учителя - М.: Мнемозина, 2008.
13. «Преподавание математики и новые компьютерные технологии» \\ «Математика в школе»,2005, №6, с.73; №7, с.56.
14., , Шевкин и начала анализа: Учеб. Для 10 кл. общеобразоват. учреждений.- М.: Просвещение, 2008, - 383 с.
15., , Шевкин и начала анализа: Учеб. Для 11 кл. общеобразоват. учреждений.- М.: Просвещение, 2008, - 448 с.
16.Саранцев обучения математике в средней школе: учебное пособие для студентов мат. спец. пед. вузов и ун-тов – М.: Просвещение, 2005. – 224 с.
17.Сборник нормативных документов. Математика/ сост. , .- М.: Дрофа, 20с.
18., Ткачева алгебры и начал математического анализа в 10 классе: кн. Для учителя. – М.: Просвещение, 2008. – 190 с.
19. О прикладной ориентации курса математики \\ «Математика в школе», 2007, №6, с.2; №7, с.2.
20.Фридман основы методики обучения математике: Учебное пособие. –М.: Едиториал УРСС, 2005.-248 с.
21.Фридман научиться решать задачи: Кн. для учащихся 10-11 классов. – М.: Просвещение,2004..
22.Юнина качественного обучения в школе. Учебно-методическое пособие – М.: Педагогическое общество России, 20с.
23. . Психологические основы математического образования: Учеб. Пособие для студ. Пед. Вузов – М.: Издательский центр «Академия». -2004, -320 с.
Дополнительная литература.
1. Башмаков и профиль школьного математического образования // Математика в школе№ 2.
2. Математика и математическое образование в современном мире. - М.: Просвещение, 1985.
3. Изюмова мнемических способностей и дифференциация обучения. – М.: Наука, 1995, - 382 с.
4. Концепция профильного обучения на старшей ступени общего образования // Вестник образования. – 2002. – декабрь № 4.
5. Концепция модернизации российского образования на период до 2010 года // Вестник образования. – 2002. –№ 6. – с. 11-40.
6. Унт Инге. Индивидуализация и дифференциация обучения. - М.: Педагогика, 1990.
7. Фридман -педагогические основы обучения математике в школе. - М.: Просвещение, 1983.
Внеурочная работа
Внеклассная работа по математике в средней общеобразовательной школе (на примере одного класса)
Понятие о внеклассной работе по математике, ее цели и задачи.
Характеристика основных направлений внеклассной работы. Различные формы внеклассной работы: школьные кружки; спецкурсы (факультативы) для учащихся, читаемые по отдельным разделам математики; научные общества; школьные олимпиады и конкурсы; математические вечера; внеклассное чтение; выпуск регулярной стенной печати; радиопрограммы школьного радиоузла.
Анализ действующих учебников математики соответствующего класса на предмет выявления возможности использования различных тем на кружковых занятиях.
Разработка системы: занятий математического кружка и внеклассных мероприятий для одного класса.
Литература: [17], [20], [57], [67], [92], [137], [190], [194], [236], [257], [276].
Дополнительная литература
Пропедевтика систематического курса геометрии посредством кружка «Наглядная геометрия» в 5-6 классах основной школы
Понятие пропедевтики систематического курса геометрии.
Математический кружок как средство пропедевтики систематического курса геометрии. Особенности кружковой работы с учащимися 5-6-х классов.
Анализ действующих учебников математики 5-6-х классов и учебников геометрии 7-9-х классов на предмет выявления возможности формирования и развития геометрических представлений и мышления учащихся, пропедевтики систематического курса геометрии в 5-6-х классах.
Литература: [17], [57], [64], [75], [88], [89], [90], [109], [137], [237], [265], [305], [342].
Дополнительная литература
Реализация проблемного обучения учащихся 5 класса (6, 7 класса) на кружковых занятиях по математике
Понятие проблемного обучения в математике: уровни проблемного обучения, типы проблемных ситуаций, этапы решения проблемы.
Особенности кружковой работы с учащимися 5-го (6-го, 7-го) класса. Проблемное обучение на занятиях математического кружка 5-го (6-го, 7го) класса. Анализ действующих учебников математики 5-го (6-го, 7-го) класса на предмет выявления возможности использования проблемного обучения.
Разработка материалов для математического кружка 5-го (6-го, 7-го) класса с использованием проблемного обучения (содержание и методика проведения).
Разработка варианта материалов для математического кружка по геометрии в 5-6-х классах (содержание и методика проведения).
Литература: [17], [19], [34], [47], [55], [67], [93], [132], [134], [140], [186], [190].
Дополнительная литература
Дополнительное математическое образование учащихся
5-6·классов
Понятие о дополнительном математическом образовании, его цели и задачи. Характеристика основных направлений дополнительного математического образования. Различные формы дополнительного математического образования, осуществляемого в школе, во внешкольных учебных заведениях, дома.
Использование различных средств обучения на занятиях дополнительного математического образования.
Методическая разработка одной из форм дополнительного математического образования.
Литература: [45], [79], [94], [101], [189], [190], [236], [242], [252], [276].
Дополнительная литература
Взаимосвязь урочной и внеурочной деятельности
учащихся основной школы
Понятие о внеурочной деятельности учащихся, ее цели и задачи. Различные формы внеурочной работы. Понятие взаимосвязи урочной и внеурочной деятельности учащихся, ее уровни и способы реализации.
Анализ учебников математики на предмет возможного осуществления взаимосвязи урочной и внеурочной деятельности.
Разработка системы урочных и внеурочных занятий по математике для одного класса с высоким уровнем взаимосвязи.
Литература: [57], [67], [94], [101], [105], [137], [183], [190], [252], [254], [257].
Дополнительная литература
Методика про ведения факультативного курса
«Философские вопросы неевклидовых геометрий»
Анализ психолого-педагогической литературы по проблеме факультативных занятий.
Психолого-педагогические особенности процесса обучения в системе факультативных занятий.
Психолого-педагогические основы организации факультативных занятий.
История возникновения и развития факультативов по математике их роль и место в системе курса математики средней школы.
Фуркация обучения в средней школе и ее история.
Факультативное занятие как форма дифференцированного обучения, удовлетворяющая требованиям комплексного подхода к обучению старшеклассников.
Отбор форм и методов проведения факультативных занятий по математике со старшеклассниками по теме «Философские вопросы неевклидовых геометрий».
Разработка теоретического материала и построение факультативного курса (конструирование групп занятий), отвечающего комплексному подходу к обучению по теме «Философские вопросы неевклидовых геометрий».
Исторический обзор создания неевклидовых геометрий. Развитие геометрии в школе Платона и Аристотеля. Аристотелева схема логического вывода. Система Евклида. Постулаты и аксиомы. Абсолютная и собственно евклидова геометрия.
Попытки доказательства 5 Постулата. Работы Лобачевского, Гаусса, Бойаи.
Эволюция философских представлений о пространстве: античная натурфилософия; евклидова концепция пространства; бесконечность, непрерывность и дискретность пространства у античных философов, философов Западной Европы, у Гегеля.
Программы Клейна, Римана и Картана обобщения евклидовой геометрии. Общая концепция математического пространства.
Литература: [9], [60], [61], [87], [135], [136], [145], [170], [195], [196], [243], [270], [308].
Дополнительная литература
Методика проведения факультативного курса
«Основания геометрии»
Анализ психолого-педагогической литературы по проблеме факультативных занятий.
Психолого-педагогические особенности процесса обучения в системе факультативных занятий.
Психолого-педагогические основы организации факультативных занятий.
История возникновения и развития факультативов по математике их роль и место в системе курса математики средней школы.
Фуркация обучения в средней школе и ее история.
Факультативное занятие как форма дифференцированного обучения, удовлетворяющая требованиям комплексного подхода к обучению старшеклассников
Отбор форм и методов проведения факультативных занятий по математике со старшеклассниками по теме «Основания геометрии».
Разработка теоретического материала и построение факультативного курса, отвечающего комплексному подходу к обучению по теме «Основания геометрии».
Исторический обзор развития оснований геометрии. Понятие аксиоматической теории. Анализ требований, предъявляемых к системам аксиом.
Практические основания геометрии; аксиоматические основания геометрии.
Подбор и систематизация задач.
Литература: [60], [61], [85], [135], [136], [145], [195], [243], [270].
Дополнительная литература
Методика проведения факультативного курса
«Свойства фигур на плоскости Лобачевского»
Анализ психолого-педагогической литературы по проблеме факультативных занятий.
Психолого-педагогические особенности процесса обучения в системе факультативных занятий.
Психолого-педагогические основы организации факультативных занятий.
История возникновения и развития факультативов по математике их роль и место в системе курса математики средней школы.
Фуркация обучения в средней школе и ее история.
Факультативное занятие как форма дифференцированного обучения. Отбор форм и методов проведения факультативных занятий по математике со старшеклассниками по теме «Свойства фигур на плоскости Лобачевского».
Разработка теоретического материала, включающего исторический обзор создания геометрии Лобачевского и исследование свойств плоскости Лобачевского. Построение факультативного курса по теме «Свойства фигур на плоскости Лобачевского».
Подбор и систематизация задач, позволяющих выявить существенные различия евклидовой и неевклидовой геометрий.
Литература: [60], [61], [73], [135], [136], [170], [195], [196], [245], [270], [272], [335].
Дополнительная литература
Методика проведения факультативного курса «Методы решения нестандартных задач по алгебре»
Анализ психолого-педагогической литературы по проблеме факультативных занятий.
Психолого-педагогические особенности процесса обучения в системе факультативных занятий.
Психолого-педагогические основы организации факультативных занятий.
История возникновения и развития факультативов по математике их роль и место в системе курса математики средней школы.
Фуркация обучения в средней школе и ее история.
Факультативное занятие как форма дифференцированного обучения, удовлетворяющая требованиям комплексного подхода к обучению старшеклассников.
Роль и место нестандартных задач и нестандартных методов решения в системе курса алгебры.
Отбор форм и методов проведения факультативных занятий по математике со старшеклассниками по теме «Методы решения нестандартных задач по алгебре».
Разработка теоретического материала и построение факультативного курса, отвечающего комплексному подходу к обучению по теме «Методы решения нестандартных задач по алгебре». Систематизация методов решения нестандартных задач: метод функциональной и тригонометрической подстановок, методы решения функциональных уравнений, векторный метод, методы на основе свойств функций.
Подбор и систематизация задач, решаемых нестандартными методами.
Литература: [19], [60], [61], [85], [195], [196], [213], [270], [282].
Дополнительная литература
Методика обучения решению задач с параметрами
Анализ психолого-педагогической литературы по теме исследования; психолого-педагогические основы преподавания математики в 10-11 классах с учетом возрастных особенностей учащихся.
Анализ имеющейся учебной и методической литературы по теме.
Роль подготовительных курсов при выборе специальности и в процессе подготовки к вступительным экзаменам в вузы. Особенности педагогической деятельности по профориентации учащихся.
Проблемы обучения математики в сжатые сроки. Психологопедагогические особенности обучения старшеклассников в форме глобального обобщающего повторения и систематизации.
3адачи с параметрами, их роль и место в системе курса математики средней школы.
Разработка методики обучения, позволяющей в сжатые сроки научить абитуриентов диагностировать оптимальный метод решения задачи с параметром.
Систематизация основных методов решения задач с параметром. Подбор и систематизация задач по методам и уровням сложности.
Литература: [7], [60], [61], [83], [87], [102], [165], [195], [196], [241], [308], [343].
Дополнительная литература
Методика проведения элективного курса
«Элементы наглядной топологии» в профильной школе
Анализ психолого-педагогической литературы по проблеме дифференцированного обучения. Психологическая характеристика учащихся старших классов.
Организационно-педагогические аспекты дифференцированного обучения.
Методические особенности обучения геометрии учащихся профильных классов.
Введение элективных курсов по математике в состав профиля обучения на старшей ступени школы (исторический аспект).
Роль и место элективных курсов в системе профильного обучения.
Методическое обеспечение элективного курса «Элементы наглядной топологии». Разработка теоретического и практического материала для обучения учащихся элементам наглядной топологии. Отбор содержания курса, форм и методов проведения элективных занятий элективного курса «Элементы наглядной топологии» в профильной школе.
Применение информационных технологий с целью визуализации топологических понятий.
Литература:
1. , Ефремович топология [текст]. – М.: Наука. Главная редакция физико-математической литературы, 1983.
2. , , Фоменко в топологию: Учеб. Пособие [текст].- 2-е изд.- М.: Наука. Физматлит, 1995.
3. Бутузов обучение – важное дидактическое средство эффективного обучения школьников. – М.:ИЗДАТЕЛЬСТВО, 1968.
4. Бутузов подход к обучению учащихся на современном уроке. – Новгород: ЛГПИ, 1972.
5. Гильберт Давид, Кон-Фоссен Стефан: Наглядная геометрия [текст]: Пер. с нем. Изд. 4-е, стереотипное. – М.: Едиториал УРСС, 2004. – с 289-292.
6. Гусев -педагогические основы обучения математике. – М.: Вербум-М, Академия, 2003.
7. , , Фирсов в обучении математике // Математика в школе. – 1990. – номер– с. 15-21
8. , Чмутов и их инварианты: Математическое просвещение, ?????????
9. Педагогическая энциклопедия: В 2 томах. / Под ред. , . – М.: Советская энциклопедия. – Т.1. ГОД издания
10. Прасолов топология. – М: МЦНМО, 2006.
11. , . Узлы, зацепления, косы и трёхмерные многообразия. – М.: МЦНМО, 1997.
12. Саранцев обучения математике в средней школе: Учеб. пособие для студентом мат. спец. пед. вузов и ун-тов. – М.: Просвещение, 2002.
13. Смирнова -методические основы преподавания геометрии в условиях профильной дифференциации: Монография. – М.: Прометей, 1994.
14. Сосинский и косы. – М.: МЦНМО, 2001.
15. Унт и дифференциация обучения. – М.: Педагогика, 1990.
16. Элементы топологии. Методическое пособие для студентов 5 курса математического факультета [текст] / кафедра алгебры, геометрии и методики их преподавания. Сост. . – М.: МГПУ, 2005.
17. Якиманская основы математического образования: Учеб. пособие для студ. пед. вузов. – М.: Академия, 2004.
Дополнительная литература




